-
Notifications
You must be signed in to change notification settings - Fork 4
6、四轴飞行器算法讲解
姿态解算指控制器读取自身传感器数据,实时计算四轴飞行器的姿态角,比如横滚角(roll),俯仰角(pitch),偏航角(yaw)的信息,控制器根据这些信息即可计算4个电机的输出量,使飞行器保持平衡稳定或者保持一定的倾斜角往设定方向飞行。姿态解算是飞行器飞行的关键技术之一,解算速度和精度直接关系到飞行器飞行中的稳定性和可靠性。
姿态解算的方法有很多,比较典型的方法有扩展型卡尔曼滤波算法(EKF),互补滤波算法等。扩展型卡尔曼滤波算法具有高精度的特点,但其计算量大,并要求建立精确的动力学模型,因此并不是微型四轴飞行器的最佳选择;而互补滤波算法对系统的要求相对较低,计算量也不大,在微型四轴飞行器的姿态解算中应用最广。
飞行器姿态有多种表示方式,常见的是四元数,欧拉角,矩阵和轴角。他们各自有其自身的优点,在不同的领域使用不同的表示方式。在四轴飞行器中使用到了四元数和欧拉角。
6.2.1 欧拉角
用来确定定点转动刚体位置的 3 个一组独立角参量,由章动角 θ、旋进角(即进动角) ψ 和自转角 j 组成,为莱昂哈德·欧拉首先提出而得名。
对于在三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。参考系又称为实验室参考系,是静止不动的。而坐标系则固定于刚体,随着刚体的旋转而旋转。
如图 5.2.1 所示:设定 xyz 轴为参考系的参考轴。称 xy-平面与 XY-平面的相交为交点线,用英文字母(N)代表。zxy 顺规的欧拉角可以静态地这样定义: α 是 x-轴与交点线的夹角,β 是 z-轴与 Z-轴的夹角,γ 是交点线与 X-轴的夹角。
很可惜地,对于夹角的顺序和标记,夹角的两个轴的指定,并没有任何常规。科学家对此从未达成共识。每当用到欧拉角时,我们必须明确的表示出夹角的顺序,指定其参考轴。
实际上,有许多方法可以设定两个坐标系的相对取向。欧拉角方法只是其中的一种。此外,不同的作者会用不同组合的欧拉角来描述,或用不同的名字表示同样的欧拉角。因此,使用欧拉角前,必须先做好明确的定义。
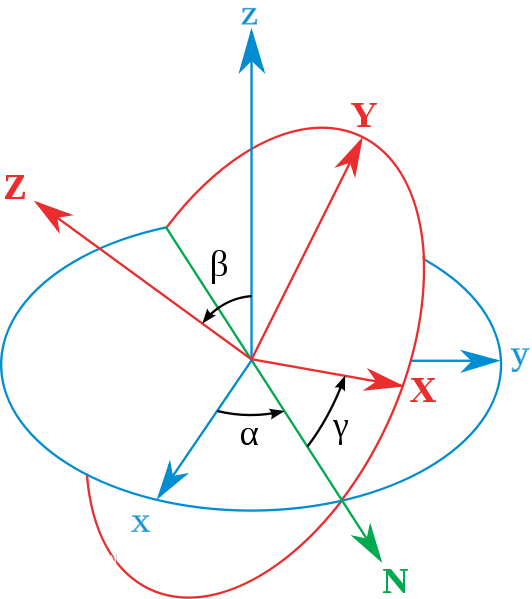
图 5.2.1 欧拉角
本小节内容部分摘自百度百科-欧拉角
四元数(Quaternions)是由爱尔兰数学家哈密顿(William Rowan Hamilton,1805-1865)在 1843年发明的数学概念。明确地说,四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话,四元数就代表着一个四维空间,相对于复数为二维空间。
单位四元数与欧拉角、旋转矩阵是等价的,但又不同于欧拉角表示,四元数表示法没有奇异点的问题,正因为这个优点,单位四元数在姿态估计的核心算法中非常常见。比起三维旋转矩阵四元数更能方便的给出旋转的转轴和旋转角。
关于四元数的计算,四元数可以理解为一个实数和一个向量的组合,也可以理解为四维的向量。这里用一个圈表示 q 是一个四元数(很可能不是规范的表示方式)。
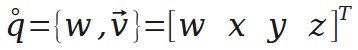
四元数的长度(模)与普通向量相似。
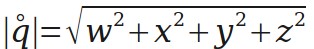
下面是对四元数的单位化,单位化的四元数可以表示一个旋转。
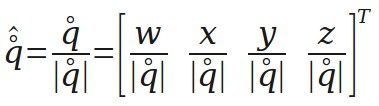
四元数相乘,旋转的组合就靠它了。
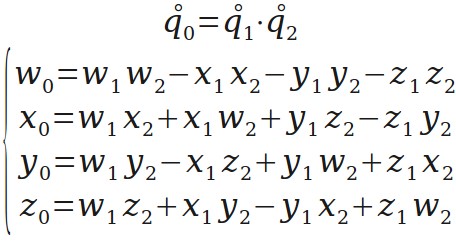
旋转的“轴角表示”转“四元数表示”。这里创造一个运算 q(w,θ),用于把绕单位向量 w 转 θ 角的旋转表示为四元数。
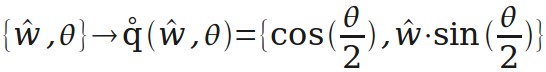
通过 q(w,θ),引伸出一个更方便的运算 q(f,t)。有时需要把向量 f 的方向转到向量 t 的方向,这个运算就是生成表示对应旋转的四元数的(后面会用到)。
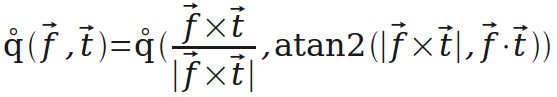
然后是“四元数表示”转“矩阵表示”。再次创造运算,用 R(q)表示四元数 q 对应的矩阵(后面用到)。
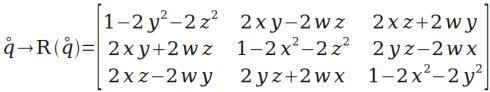
多个旋转的组合可以用四元数的乘法来实现。
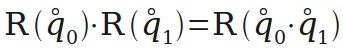
“四元数表示”转“欧拉角表示”。用于显示。

本小节内容部分摘自百度百科-四元数
我们先来看看如何用欧拉角描述一次平面旋转(坐标变换),如图 5.3.1 所示:
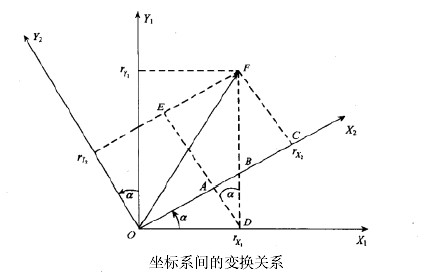
图 5.3.1 欧拉角平面旋转
设坐标系绕旋转 α 角后得到坐标系,在空间中有一个矢量在坐标系中的投影为,在内的投影为由于旋转绕进行,所以 Z 坐标未变,即有:
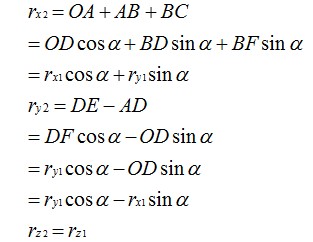
转换成矩阵形式表示为:
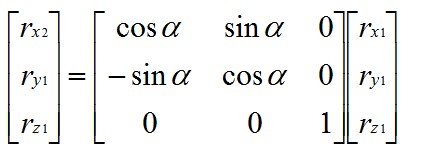
整理一下:
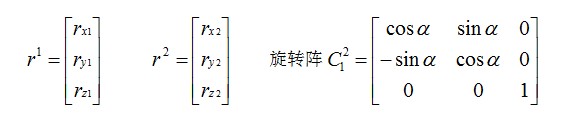
上面仅仅是绕一根轴的旋转,如果三维空间中的欧拉角旋转要转三次:

上面得到了一个表示旋转的方向余弦矩阵,不过要想用欧拉角解算姿态,其实我们套用欧拉角微分方程就行了:
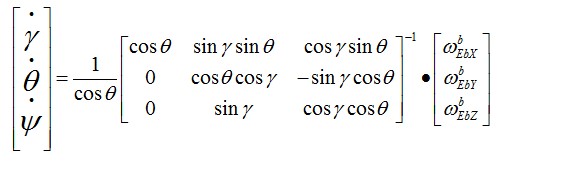
上式中左侧是本次更新后的欧拉角,对应 roll、pitch、yaw。右侧是上个周期测算出来的角度,三个角速度由直接安装在四轴飞行器的三轴陀螺仪在这个周期转动的角度,单位为弧度,计算间隔时间T 陀螺角速度,比如0.02 秒0.01 弧度/秒=0.0002 弧度。间因此求解这个微分方程就能解算出当前的欧拉角。
前面介绍了什么是欧拉角,而且欧拉角微分方程解算姿态关系简单明了,概念直观容易理解,那么我们为什么不用欧拉角来表示旋转而要引入四元数呢?
一方面是因为欧拉角微分方程中包含了大量的三角运算,这给实时解算带来了一定的困难。而且当俯仰角为90度时方程式会出现神奇的“GimbalLock”。所以欧拉角方法只适用于水平姿态变化不大的情况,而不适用于全姿态飞行器的姿态确定。
四元数法只求解四个未知量的线性微分方程组,计算量小,易于操作,是比较实用的工程方法。
我们知道在平面(x,y)中的旋转可以用复数来表示,同样的三维中的旋转可以用单位四元数来描述。我们来定义一个四元数:
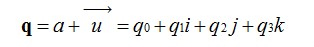
我们可以把它写成,其中,。那么是矢量,表示三维空间中的旋转轴。w是标量,表示旋转角度。那么就是绕轴旋转 w 度,所以一个四元数可以表示一个完整的旋转。只有单位四元数才可以表示旋转,至于为什么,因为这就是四元数表示旋转的约束条件。
而刚才用欧拉角描述的方向余弦矩阵用四元数描述则为:
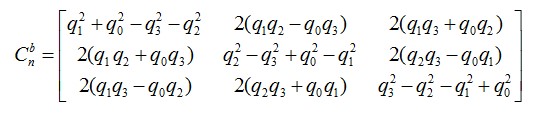
更多参考资料请看:
秦永元《惯性导航》 袁信、郑锷的《捷联式惯性导航原理》,邓正隆的《惯性技术》
当今的闭环自动控制技术都是基于反馈的概念以减少不确定性。反馈理论的要素包括三个部分:测量、比较和执行。测量关键的是被控变量的实际值,与期望值相比较,用这个偏差来纠正系统的响应,执行调节控制。在工程实际中,应用最为广泛的调节器控制规律为比例、积分、微分控制,简称 PID 控制,又称 PID 调节。
PID 控制器(比例-积分-微分控制器)是一个在工业控制应用中常见的反馈回路部件,由比例单元 P、积分单元 I 和微分单元 D 组成。PID 控制的基础是比例控制;积分控制可消除稳态误差,但可能增加超调;微分控制可加快大惯性系统响应速度以及减弱超调趋势。这个理论和应用的关键是,做出正确的测量和比较后,如何才能更好地纠正系统。
PID(比例(proportion)、积分(integral)、导数(derivative))控制器作为最早实用化的控制器已有近百年历史,现在仍然是应用最广泛的工业控制器。PID 控制器简单易懂,使用中不需精确的系统模型等先决条件,因而成为应用最为广泛的控制器,典型的单级 PID 控制器如图 5.4.1 所示:
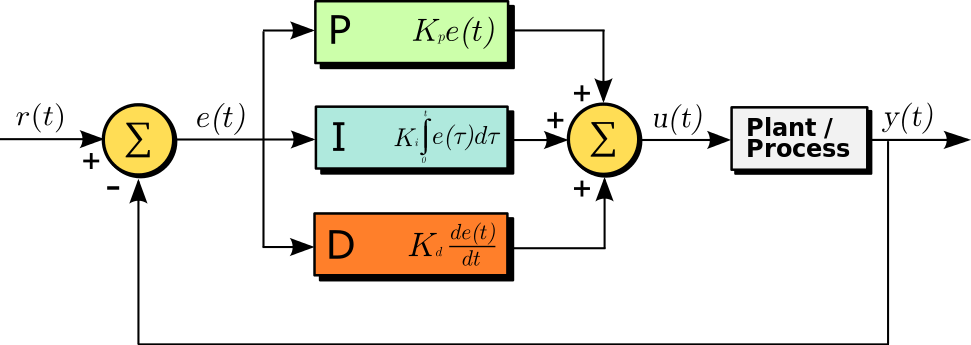
图 5.4.1 单级 PID 控制器结构框图比例(P)控制
比例控制是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系。当仅有比例控制时系统输出存在稳态误差。比例项输出:
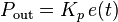
不同比例增益 Kp 下,受控变量的阶跃响应(Ki,Kd 维持稳定值)如图 5.4.2 所示:
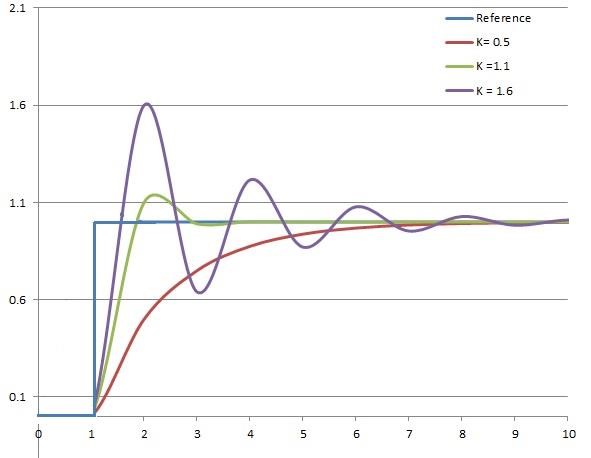
图 5.4.2 不同比例增益下,系统对阶跃信号的响应积分(I)控制
在积分控制中,控制器的输出与输入误差信号的积分成正比关系。对于只有比例控制的系统存在稳态误差,为了消除稳态误差,在控制器中必须引入“积分项”。积分项是误差对时间的积分,随着时间的增加,积分项会增大。这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。因此,比例积分(PI)控制器,可以使系统在进入稳态后无稳态误差。 积分项输出:
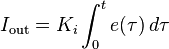
不同积分增益 Ki 下,受控变量的阶跃响应(Kp,Kd 维持稳定值)如图 5.4.3 所示:
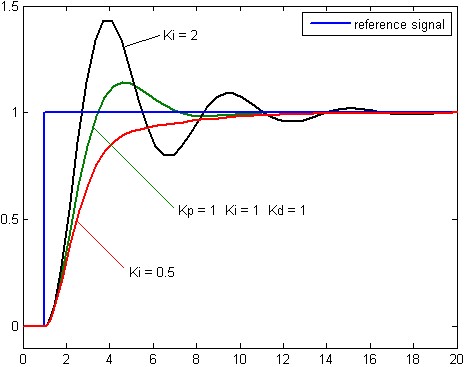
图 5.4.3 不同积分增益下,系统对阶跃信号的响应微分(D)控制
在微分控制中,控制器的输出与输入误差信号的微分成正比关系。微分调节就是偏差值的变化率。使用微分调节能够实现系统的超前控制。如果输入偏差值线性变化,则在调节器输出侧叠加一个恒定的调节量。大部分控制系统不需要调节微分时间。因为只有时间滞后的系统才需要附加这个参数。微分项输出:
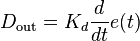
不同微分增益 Kd 下,受控变量的阶跃响应(Kp,Ki 维持稳定值)如图 5.4.4 所示:
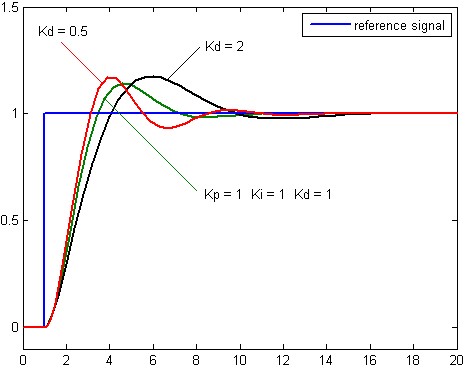
图 5.4.4 不同微分增益下,系统对阶跃信号的响应
综上可得到 PID 控制数学表达式:
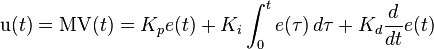
更多内容请参考维基百科-PID_controller。
单级 PID 控制框图,如图 5.5.1 所示:

图 5.5.1 单级 PID 框图
期望角度就是遥控器控制飞行器的角度值,反馈当前角度就是传感器测得的飞行器角度,这里的角度指的是 Roll/Pitch/Yaw 三个角度,而且在 PID 控制计算的时候,是相互独立的。
角度单环 PID 控制算法仅仅考虑了飞行器的角度信息,如果想增加飞行器的稳定性(增加阻尼)并提高它的控制品质,我们可以进一步的控制它的角速度,于是角度/角速度-串级 PID 控制算法应运而生。在这里,相信大多数朋友已经初步了解了角度单环 PID 的原理,但是依旧无法理解串级 PID 究竟有什么不同。其实很简单:它就是两个 PID 控制算法,只不过把他们串起来了(更精确的说是套起来)。那这么做有什么用?答案是,它增强了系统的抗干扰性(也就是增强稳定性),因为有两个控制器控制飞行器,它会比单个控制器控制更多的变量,使得飞行器的适应能力更强。
串级 PID 控制框图,如图 5.5.2 所示:
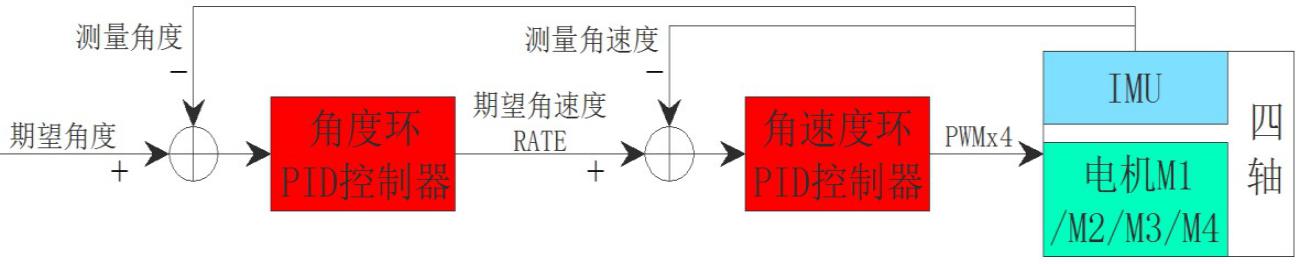
图 5.5.2 串级 PID 框图
期望角度来自遥控数据,反馈角度来自传感器,二者的偏差作为外环角度环的输入,角度环 PID 输出角速度的期望值;角速度期望值减去传感器反馈的角速度得到角速度偏差值,这个值作为内环角速度环的输入,角速度环 PID 输出姿态控制量,控制量转换为 PWM 去控制电机,从而控制四轴。
内环 P:从小到大,拉动四轴越来越困难,越来越感觉到四轴在抵抗你的拉动;到比较大的数值时,四轴自己会高频震动,肉眼可见,此时拉扯它,它会快速的振荡几下,过几秒钟后稳定;继续增大,不用加人为干扰,自己发散翻机。特别注意:只有内环 P 的时候,四轴会缓慢的往一个方向下掉,这属于正常现象。这就是系统角速度静差。
内环 I:前述 PID 原理可以看出,积分只是用来消除静差,因此积分项系数个人觉得没必要弄的很大,因为这样做会降低系统稳定性。从小到大,四轴会定在一个位置不动,不再往下掉;继续增加 I 的值,四轴会不稳定,拉扯一下会自己发散。特别注意:增加 I 的值,四轴的定角度能力很强,拉动他比较困难,似乎像是在钉钉子一样,但是一旦有强干扰,它就会发散。这是由于积分项太大,拉动一下积分速度快,给的补偿非常大,因此很难拉动,给人一种很稳定的错觉。
内环 D:这里的微分项 D 为标准的 PID 原理下的微分项,即本次误差-上次误差。在角速度环中的微分就是角加速度,原本四轴的震动就比较强烈,引起陀螺的值变化较大,此时做微分就更容易引入噪声。因此一般在这里可以适当做一些滑动滤波或者 IIR 滤波。从小到大,飞机的性能没有多大改变,只是回中的时候更加平稳;继续增加 D 的值,可以肉眼看到四轴在平衡位置高频震动(或者听到电机发出滋滋的声音)。前述已经说明 D 项属于辅助性项,因此如果机架的震动较大,D 项可以忽略不加。
外环 P:当内环 PID 全部整定完成后,飞机已经可以稳定在某一位置而不动了。此时内环 P,从小到大,可以明显看到飞机从倾斜位置慢慢回中,用手拉扯它然后放手,它会慢速回中,达到平衡位置;继续增大 P 的值,用遥控器给不同的角度给定,可以看到飞机跟踪的速度和响应越来越快;继续增加 P 的值,飞机变得十分敏感,机动性能越来越强,有发散的趋势。