README.md

1245. 树的直径

English Version

题目描述

给你这棵「无向树」，请你测算并返回它的「直径」：这棵树上最长简单路径的 边数。

我们用一个由所有「边」组成的数组 edges 来表示一棵无向树，其中 edges[i] = [u, v] 表示节点 u 和 v 之间的双向边。

树上的节点都已经用 {0, 1, ..., edges.length} 中的数做了标记，每个节点上的标记都是独一无二的。

 

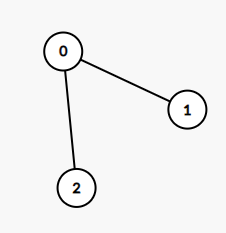
示例 1：

输入：edges = [[0,1],[0,2]]
输出：2
解释：
这棵树上最长的路径是 1 - 0 - 2，边数为 2。

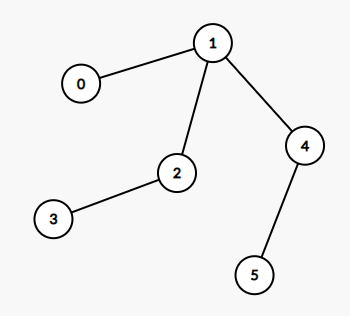
示例 2：

输入：edges = [[0,1],[1,2],[2,3],[1,4],[4,5]]
输出：4
解释： 
这棵树上最长的路径是 3 - 2 - 1 - 4 - 5，边数为 4。

 

提示：

• 0 <= edges.length < 10^4
• edges[i][0] != edges[i][1]
• 0 <= edges[i][j] <= edges.length
• edges 会形成一棵无向树

解法

两次 DFS。

首先对任意一个结点做 DFS 求出最远的结点，然后以这个结点为根结点再做 DFS 到达另一个最远结点。第一次 DFS 到达的结点可以证明一定是这个图的直径的一端，第二次 DFS 就会达到另一端。下面来证明这个定理。

定理：在一个连通无向无环图中，以任意结点出发所能到达的最远结点，一定是该图直径的端点之一。

证明：假设这条直径是 δ(s, t)。分两种情况：

1. 当出发结点 y 在 δ(s, t) 时，假设到达的最远结点 z 不是 s, t 中的任一个。这时将 δ(y, z) 与不与之重合的 δ(y, s) 拼接（也可以假设不与之重合的是直径的另一个方向），可以得到一条更长的直径，与前提矛盾。

2. 当出发结点 y 不在 δ(s, t) 上时，分两种情况：

   • 当 y 到达的最远结点 z 横穿 δ(s, t) 时，记与之相交的结点为 x。此时有 δ(y, z) = δ(y, x) + δ(x, z)。而此时 δ(y, z) > δ(y, t)，故可得 δ(x, z) ＞ δ(x, t)。由 1 的结论可知该假设不成立。
   • 当 y 到达的最远结点 z 与 δ(s, t) 不相交时，定义从 y 开始到 t 结束的简单路径上，第一个同时也存在于简单路径 δ(s, t) 上的结点为 x，最后一个存在于简单路径 δ(y, z) 上的结点为 x’。如下图。那么根据假设，有 δ(y, z) ≥ δ(y, t) => δ(x', z) ≥ δ(x', x) + δ(x, t)。既然这样，那么 δ(x, z) ≥ δ(x, t)，和 δ(s, t) 对应着直径这一前提不符，故 y 的最远结点 z 不可能在 s 到 t 这个直径对应的路外面。
   

因此定理成立。

相似题目：1522. N 叉树的直径

Python3

class Solution:
    def treeDiameter(self, edges: List[List[int]]) -> int:
        def dfs(u, t):
            nonlocal ans, vis, d, next
            if vis[u]:
                return
            vis[u] = True
            for v in d[u]:
                dfs(v, t + 1)
            if ans < t:
                ans = t
                next = u

        d = defaultdict(set)
        vis = [False] * (len(edges) + 1)
        for u, v in edges:
            d[u].add(v)
            d[v].add(u)
        ans = 0
        next = 0
        dfs(edges[0][0], 0)
        vis = [False] * (len(edges) + 1)
        dfs(next, 0)
        return ans

Java

class Solution {
    private Map<Integer, Set<Integer>> g;
    private boolean[] vis;
    private int next;
    private int ans;

    public int treeDiameter(int[][] edges) {
        int n = edges.length;
        ans = 0;
        g = new HashMap<>();
        for (int[] e : edges) {
            g.computeIfAbsent(e[0], k -> new HashSet<>()).add(e[1]);
            g.computeIfAbsent(e[1], k -> new HashSet<>()).add(e[0]);
        }
        vis = new boolean[n + 1];
        next = edges[0][0];
        dfs(next, 0);
        vis = new boolean[n + 1];
        dfs(next, 0);
        return ans;
    }

    private void dfs(int u, int t) {
        if (vis[u]) {
            return;
        }
        vis[u] = true;
        if (ans < t) {
            ans = t;
            next = u;
        }
        for (int v : g.get(u)) {
            dfs(v, t + 1);
        }
    }
}

C++

class Solution {
public:
    unordered_map<int, unordered_set<int>> g;
    vector<bool> vis;
    int ans;
    int next;

    int treeDiameter(vector<vector<int>>& edges) {
        for (auto& e : edges) {
            g[e[0]].insert(e[1]);
            g[e[1]].insert(e[0]);
        }
        int n = edges.size();
        ans = 0;
        vis.resize(n + 1);
        next = edges[0][0];
        dfs(next, 0);
        vis.assign(vis.size(), false);
        dfs(next, 0);
        return ans;
    }

    void dfs(int u, int t) {
        if (vis[u]) return;
        vis[u] = true;
        if (ans < t) {
            ans = t;
            next = u;
        }
        for (int v : g[u]) dfs(v, t + 1);
    }
};

Go

func treeDiameter(edges [][]int) int {
	n := len(edges)
	g := make(map[int][]int)
	for _, e := range edges {
		g[e[0]] = append(g[e[0]], e[1])
		g[e[1]] = append(g[e[1]], e[0])
	}
	vis := make(map[int]bool, n+1)
	ans := 0
	next := edges[0][0]
	var dfs func(u, t int)
	dfs = func(u, t int) {
		if vis[u] {
			return
		}
		vis[u] = true
		if ans < t {
			ans = t
			next = u
		}
		if vs, ok := g[u]; ok {
			for _, v := range vs {
				dfs(v, t+1)
			}
		}
	}
	dfs(next, 0)
	vis = make(map[int]bool, n+1)
	dfs(next, 0)
	return ans
}

...