-
Notifications
You must be signed in to change notification settings - Fork 54
1_时序基础概念演示
ChannelCMT edited this page Jun 25, 2019
·
1 revision
- 读取数据
- 检验原始数据平稳性
- 差分
- 检验差分平稳性
- p-value
# 读取数据
import pandas as pd
data = pd.read_excel('./HFData.xlsx').set_index('datetime')Dickey-Fuller的零假设是有一个单位根,另一种假设是没有单位根。如果pvalue大于一个临界大小,那么我们不能拒绝有一个单位根。
from statsmodels.tsa.stattools import adfuller
print('原始序列的检验结果为:',adfuller(data['close'].dropna().values))
print('原始序列p-value结果为:',adfuller(data['close'].dropna().values)[1]) D:\Anaconda3\lib\site-packages\statsmodels\compat\pandas.py:56: FutureWarning: The pandas.core.datetools module is deprecated and will be removed in a future version. Please use the pandas.tseries module instead.
from pandas.core import datetools
原始序列的检验结果为: (-2.1141723681990077, 0.23885413973689235, 24, 8663, {'1%': -3.4311050777703302, '5%': -2.8618736937872296, '10%': -2.566947620253096}, 57380.39848402708)
原始序列p-value结果为: 0.23885413973689235
# 进行差分
data['diffClose'] = data['close'].diff()
diffClose = data['diffClose'].dropna().values#平稳性检测
from statsmodels.tsa.stattools import adfuller
print('差分序列的p-value结果为:',adfuller(diffClose)[1]) 差分序列的p-value结果为: 3.847990367587417e-29
- ACF
- PACF
import matplotlib.pyplot as plt
import statsmodels.api as smfig = plt.figure(figsize=(12,8))
ax1=fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(data.close,lags=10,ax=ax1)#自相关系数图
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(data.close,lags=10,ax=ax2)#偏自相关系数图
plt.show()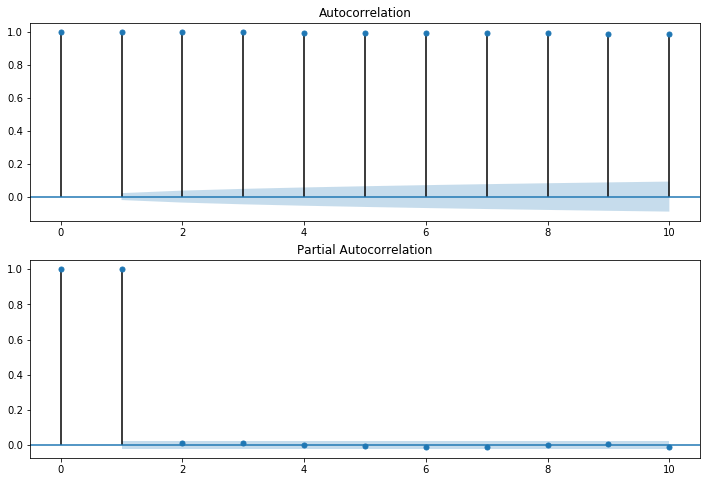
# 观察处理后数据的ACF和PACF
fig = plt.figure(figsize=(12,8))
ax1=fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(diffClose,lags=10,ax=ax1)#自相关系数图
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(diffClose,lags=10,ax=ax2)#偏自相关系数图
plt.show()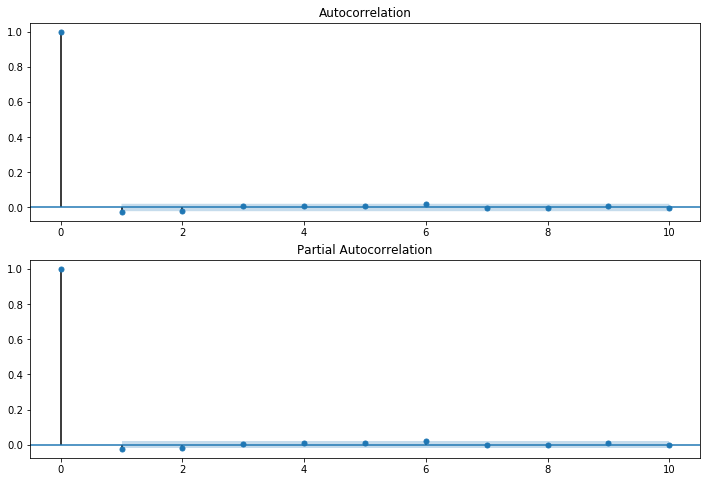
- 生成白噪声
- 生成随机游走
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
n = 500
white_noise = np.random.standard_normal(size=n)
plt.plot(white_noise)
plt.title('White Noise')
plt.show()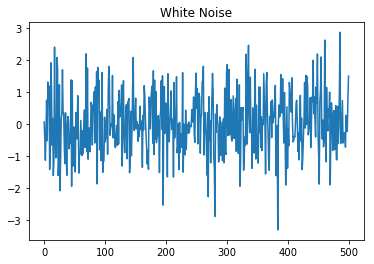
import matplotlib.pyplot as plt
import numpy as np
nwalks = 5
nsteps = 200
draws = np.random.randint(0, 2, size=(nwalks, nsteps)) # 0 or 1
steps = np.where(draws > 0, 1, -1)
walks = steps.cumsum(1)
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(nwalks):
ax.plot(walks[i])
plt.show()
steps = np.random.normal(loc=0, scale=2, size=(nwalks, nsteps))
walks = steps.cumsum(1)
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(nwalks):
ax.plot(walks[i])
plt.show()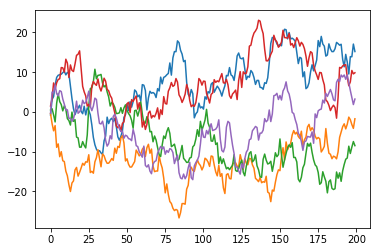
# 观察处理后数据的ACF和PACF
fig = plt.figure(figsize=(12,8))
ax1=fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(walks[0],lags=10,ax=ax1)#自相关系数图
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(walks[0],lags=10,ax=ax2)#偏自相关系数图
plt.show()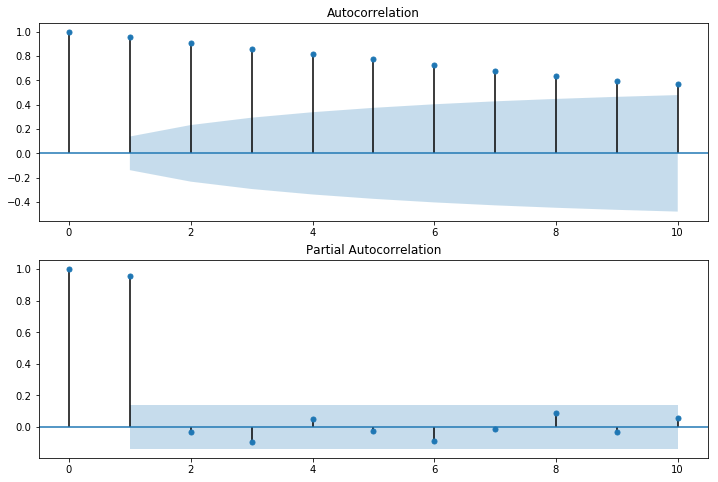
-
python基础
-
python进阶
-
数据格式处理
-
数据计算与展示
-
因子横截面排序分析
-
信号时间序列分析
-
CTA策略类型
-
附录:因子算法