I developed this study based on the logic that every integer square root is the sum of n sequential odd numbers.
The name was given because of the format the square gets: layers, from inside to outside, no spoilers, there will be examples below.
-- We can represent squares graphicaly (samples after it) and they will measure n per side, that is exactly the n odd numbers.
Examples:
sqrt(1) = 1 (1)
sqrt(4) = 2 (1+3)
sqrt(9) = 3 (1+3+5)
sqrt(16) = 4 (1+3+5+7)
...
sqrt(81) = 9 (1+3+5+7+9+11+13+15+17)
And it goes to infinity.
Using the above as our base, I was thinking: "and what about the numbers those don't have an integer root?"
Then I built this:
| Subtitles | |
|---|---|
| O | Used unity slot |
| X | Empty unity slot |
-- See the squares! There're layers!! ^_^
but, when we have 5 or 20, for example, it become:
sqrt(5) ~= 1/1 + 3/3 + 1/5 = 2.2
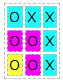
sqrt(20) ~= 1/1 + 3/3 + 5/5 + 7/7 + 4/9 = 4.4444444444444

(the divisions are => UsedUnitySlots/odd)
However, I saw that there was a considerable error in result (when you multiply the resultant number itself and compare with original) which floats between 0 and 0.25 (as you can see in 'projeção (Num x Num-(result^2))'). I percepted that last year (2018), I'll continue with this problem after.
Other trouble I found was either with numbers between 0 and 1, beacause the last layers is 1, so, the square root of 0.5 would be 0.5/1 = 0.5, but the correct is 0.707106781!
Calculating a little bit we can see that:
sqrt(0.5) = sqrt(0.5 * 100)/10
PROBLEM SOLVED!
Then I saw that, weirdly, the difference between the "canonical" root and the one I got were PRETTY lower than for the number outside this interval, so, Its finished, I FOUND THE SOLUTION FOR THE PREVIOUS PROBLEM!
sqrt(2) = 1.414213562 (CANONICAL)
sqrt(2) = 1.333333333 (MY ALGORYTHM)
sqrt(200) = 14.142135624 -> sqrt(2) = 14.142135624/10 (APPLYING THE LOGIC ABOVE)
Thinking about number's precision
As bigger the number, as bigger its root precision (using my method), FACT.
BUT, WHY?
Because a big odd means more slots to be filled. "Increasing the ruler we increase the measurement".
Samples:
1/2 ~= 7/12
0.5 ~= 0.5888888888
HOW TO IMPLEMENT THIS CODE?
Clone this repository, move sqrt.py to your project directory, then:
from sqrt import sqrt
...
root = sqrt(num)
___________________________________________________________________________________________
THANK YOU
I'm thankful for your attention, questions, critics or suggestions, call me:[email protected] ;)
O estudo que desenvolvi é baseado na premissa de que toda raíz quadrada de um número com raíz inteira é a soma de n números ímpares consecutivos.
O nome dado ao método deve-se à construção de quadrados por camadas, de dentro pra fora, sem spoilers, tem exemplos sobre isso abaixo.
-- Podemos representar os quadrados graficamente (exemplos mais abaixo) de modo que terão lado n, que coincide com os n números ímpares.
Exemplos:
sqrt(1) = 1 (1)
sqrt(4) = 2 (1+3)
sqrt(9) = 3 (1+3+5)
sqrt(16) = 4 (1+3+5+7)
...
sqrt(81) = 9 (1+3+5+7+9+11+13+15+17)
e assim sucessivamente.
Tomando o explicado acima como alicerce, indaguei-me: "e os números que não tem raíz certa?"
Pensei na seguinte coisa:
| Legendas | |
|---|---|
| O | Unidade preenchida |
| X | Unidade vaga |
-- Observe os quadrados, eis as camadas ^_^
mas, quando temos 5 ou 20, por exemplo, fica:
sqrt(5) ~= 1/1 + 3/3 + 1/5 = 2.2

sqrt(20) ~= 1/1 + 3/3 + 5/5 + 7/7 + 4/9 = 4.4444444444444

(as frações são => espaçosOcupados/ímpar)
Todavia, percebi que havia uma margem de erro na raiz (quando se eleva ela ao quadrado e compara com o número original) que tende de 0 a 0.25 (como observável no gráfico 'projeção (Num x Num-(result^2))'). Isso foi notado no ano passado (2018), continuarei com isso mais a frente.
Outro problema encontrado foi também com os números entre 0 e 1, pois, a menor camada seria 1 logo, a raiz de 0.5, por exemplo, seria 0.5/1, ou seja, ele mesmo quando deveria ser 0.707106781!
Algebrando um pouco podemos perceber que:
sqrt(0.5) = sqrt(0.5 * 100)/10
PROBLEMA RESOLVIDO!
Notei então que, estranhamente, a diferença entre a raíz "canônica" que eu obtive era MUITO menor que nos número que não estavam entre 0 e 1, e, PRONTO, A SOLUÇÃO PRO PEPINO ANTERIOR VEIO-ME!
sqrt(2) = 1.414213562 (CANÔNICO)
sqrt(2) = 1.333333333 (MEU ALGORITMO)
sqrt(200) = 14.142135624 -> sqrt(2) = 14.142135624/10 (APLICANDO A LÓGICA ANTERIOR)
Ensaio sobre a precisão dos números
Quanto maior o número, maior será a precisão da sua raíz (pelo meu método), FATO.
POR QUÊ?
Pois, quanto maior for o número, mais ímpares serão aplicados sobre ele e, quanto maior numerador de uma fração, melhor a sua demonstração do número real desejado, "Quanto mais detalhada a régua, melhor a medição".
Exemplo:
1/2 ~= 7/12
0.5 ~= 0.5888888888
COMO IMPLEMENTAR O ALGORITMO?
Clone o repositório, mova o sqrt.py para o diretório do seu projeto, ai então use:
from sqrt import sqrt
...
root = sqrt(num)
OBRIGADO
Obrigado pela atenção, duvidas, críticas ou sugestões, contacte-me: [email protected] ;)