This is an implementation of two Spring-embedder algorithms used for graph layout: Force-directed (Fruchterman - Reingold) and Local minimum energy (Kamada- Kawaii) in C language.
Generate matrix vertexes and edges:
make
.\MyForce
Draw graph:
cd drawgraph
qmake
make
.\release\drawgraph
Понятие неориентированного графа является основным в теории графов, в частности в так называемой математической теории графов. Существуют несколько определений графа, в общем случае графом можно называться пара ∈ (V, E), где V – множество вершин графа, а E – множество ребер. Две вершины v и u образуют ребро графа, если {v, u} ∈ E. Если {v, u} ∈ E следует, что {u, v} ∈ E, то граф является неориентированным. В противном случае это ориентированный граф.
Визуализация графа или сетевой диаграммы — это графическое представление вершин и ребер графа. Визуализация не следует путать с самим графом: одному и тому же графу могут соответствовать очень разные раскладки.
Для визуализации графов было определено множество различных показателей качества в попытке найти объективные средства оценки их эстетики и удобства использования. В дополнение к руководству выбором между различными методами раскладки для одного и того же графа, некоторые методы раскладки пытаются напрямую оптимизировать эти меры.
- Меньшее количество пересечений ребер: выравнивание вершин и ребер для получения наименьшего количества пересечений ребер делает график более аккуратным и менее запутанным.
- Минимум наложений вершин и рёбер.
- Распределение вершин и/или рёбер равномерно.
- Смежные вершины близки друг к другу, несмежные далеки.
- Сообщества группируются в кластеры.
Сообщества являются свойством многих сетей, в которых конкретная сеть может иметь несколько сообществ, так что узлы внутри сообщества тесно связаны. Узлы в нескольких сообществах могут перекрываться.
Также нам потребуется некоторая числовая характеристика, которая описывает выраженность структуры сообществ в данном графе, называемая модулярностью:
где δ(Ci, Cj) — дельта-функция, равная единице, если Ci = Cj и нулю иначе.
Попытаемся понять, что она означает. Возьмём две произвольные вершины i и j Вероятность появления ребра между ними при генерации случайного графа с таким же количеством вершин и рёбер, как у исходного графа, равна didj/2m. Реальное количество рёбер в сообществе C будет равняться Σi,j ∈ C Ai,j.
Таким образом, модулярность равна разности между долей рёбер внутри сообщества при данном разбиении и долей рёбер, если бы они были случайно сгенерированы. Поэтому она показывает выраженность сообществ (случайный граф структуры сообществ не имеет). Также стоит отметить, что модулярность равна 1 для полного графа, в котором все вершины помещены в одно сообщество и равна нулю для разбиения на сообщества, при котором каждой вершине сопоставлено по отдельному сообществу. Для особо неудачных разбиений модулярность может быть отрицательной.
Для каждой пары вершин связного графа можно вычислить кратчайший путь, их соединяющий. Будем считать, что каждый такой путь имеет вес, равный 1/N, где N — число возможных кратчайших путей между выбранной парой вершин. Если такие веса посчитать для всех пар вершин, то каждому ребру можно поставить в соответствие значение Edge betweenness — сумму весов путей, прошедших через это ребро.
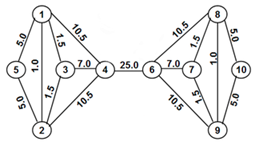
Для ясности приведём следующую иллюстрацию:
Граф, для ребёр которого посчитаны значения Edge betweenness В данном графе хочется выделить два сообщества: с вершинами 1-5 и 6-10. Граница же будет проходить через ребро, имеющее максимальный вес, 25. На этой идее и основывается алгоритм: поэтапно удаляем ребра с наибольшим весом, а оставшиеся компоненты связности объявляем сообществами. Алгоритм состроит из 6 этапов:
- Инициализировать веса
- Удалить ребро с наибольшим весом
- Пересчитать веса для ребёр
- Сообществами считаются все компоненты связности
- Посчитать функционал модулярности
- Повторять с шаги 2-6, пока есть рёбра
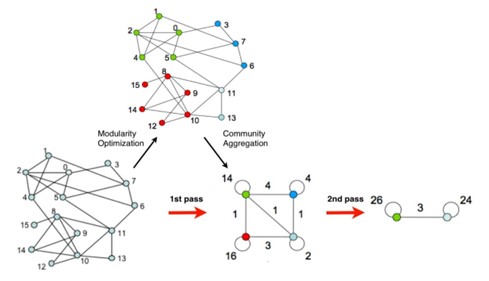
Илюстрация работы алгоритма Multilevel: два прохода, для первого показаны оба этапа
Алгоритм основан на оптимизации модулярности. Как и в многих предыдущих методах, каждой вершине сначала ставится в соответствие по сообществу. Далее чередуются следующие этапы:
- Первый этап
- Для каждой вершины перебираем её соседей
- Перемещаем в сообщество соседа, при котором модулярность увеличивается максимально
- Если перемещение в любое другое сообщество может только уменьшить модулярность, то вершина остаётся в своём сообществе
- Последовательно повторяем, пока какое-либо улучшение возможно
- Второй этап
- Создать метаграф из сообществ-вершин. При этом рёбра будут иметь веса, равные сумме весов всех рёбер из одного сообщества в другое или внутри сообщества (т.е. будет взвешенная петля)
- Перейти на первый этап для нового графа
Алгоритм прекращает работу, когда на обоих этапах модулярность не поддаётся улучшению. Все исходные вершины, которые входят в финальную метавершину, принадлежат одному сообществу. Несколько замечаний:
- На первом этапе вершина может рассматриваться несколько раз
- Порядок перебора не сильно влияет на точность, однако может существенно влиять на время работы алгоритма
- На практике оказывается достаточно 3-4 итераций
Рисование общих неориентированных графов представляет собой сложную область для различных алгоритмов рисования графов. Они должны соответствовать одному или обоим из двух важных требований: (1) хорошо рисовать график и (2) рисовать его быстро. Чтобы выполнить первое требование, алгоритмы могут следовать нескольким широко используемым эвристикам. Чтобы соответствовать второму, алгоритмы, возможно, должны масштабироваться, чтобы иметь возможность обрабатывать большой граф.
Рисование неориентированных графов можно проследить до метода проектирования СБИС, называемого силовым размещением, целью которого является оптимизация схемы схемы с наименьшим количеством пересечений линий. Eades (1984) ввел модель Spring-Embedder, в которой вершины в графе заменяются стальными кольцами, а каждое ребро заменяется пружиной. Пружинная система запускается со случайным начальным состоянием, и вершины соответственно перемещаются под действием пружинных сил. Оптимальная компоновка достигается за счет того, что энергия системы сводится к минимуму.
Эта интуитивная идея вдохновила многие последующие работы по рисованию неориентированных графов, особенно Камада и Каваи (1989), Фрухтерман и Рейнгольд (1991). Здесь их работы обобщаются и сравниваются, чтобы проиллюстрировать влияние модели Spring-Embedder на рисование графиков и визуализацию информации. Идеи, вдохновленные этими работами, бесценны для визуализации информации в целом.
Модель spring-embedder была первоначально предложена Eades (1984) и в настоящее время является одним из самых популярных алгоритмов для рисования неориентированных графов с прямолинейными ребрами, широко используемого в системах визуализации информации за его простоту и интуитивно понятную привлекательность.
Алгоритм Идеса следует двум эстетическим критериям: равномерная длина ребер и максимально возможная симметрия. В модели Spring-Embedder вершины графа обозначаются набором колец, и каждая пара колец соединена пружиной. Пружина связана с двумя видами сил: силами притяжения и силами отталкивания, в зависимости от расстояния и свойств соединительного пространства.
Рисунок графика приближается к оптимальному по мере уменьшения энергии пружинной системы. К узлам, соединенным пружиной, приложена сила притяжения (fa), а к разъединенным узлам приложена сила отталкивания (fr). Эти силы определяются следующим образом:
ka и kr — константы, а d — текущее расстояние между узлами. Для соединенных узлов это расстояние d является длиной пружины. Начальная компоновка графа настраивается случайным образом. В каждой итерации силы рассчитываются для каждого узла, и узлы соответственно перемещаются, чтобы уменьшить напряжение. Согласно Eades (1984), модель Spring Embedder работала очень быстро на VAX 11/780 на графах с числом узлов до 30. Однако модель Spring-Embedder может не работать на очень больших графах.
Модель spring-embedder вдохновила на создание ряда модифицированных и расширенных алгоритмов рисования неориентированных графов. Например, силы отталкивания обычно вычисляются между всеми парами вершин, а силы притяжения могут быть рассчитаны только между соседними вершинами. Упрощенная модель уменьшает временную сложность: вычисление сил притяжения между соседями выполняется O(|E|), хотя вычисление силы отталкивания выполняется до O(|V|²), что в целом является большим узким местом алгоритмов с n телами. Камада и Каваи (1989) представили алгоритм, основанный на модели пружинного внедрения Идса, который пытается достичь следующих двух критериев или эвристик рисования графа:
- Количество пересечений ребер должно быть минимальным.
- Вершины и ребра распределены равномерно.
Цель алгоритма состоит в том, чтобы найти локальный минимум энергии в соответствии с вектором градиента σ = 0, что является необходимым, но не достаточным условием глобального минимума. С точки зрения вычислительной сложности, такой поиск требует большого количества операций, поэтому в реализацию часто включаются дополнительные элементы управления, чтобы гарантировать, что пружинная система не окажется в ловушке в долине локального минимума.
В отличие от алгоритма Идеса, который явно не включает закон Гука, алгоритм Камады и Каваи перемещает вершины в новые положения по одной, так что общая энергия пружинной системы уменьшается с новой конфигурацией. Он также вводит понятие желаемого расстояния между вершинами на чертеже: расстояние между двумя вершинами пропорционально длине кратчайшего пути между ними.
Следуя обозначениям Камады и Каваи (1989), для динамической системы из n частиц, соединенных между собой пружинами, пусть p1, p2 ... pn будут частицами в области рисунка, соответствующими вершинам v1, v2 ... vn V соответственно. . Сбалансированное расположение вершин может быть достигнуто с помощью динамически сбалансированной пружинной системы. Камада и Каваи сформулировали степень дисбаланса как общую энергию пружин:
Их модель подразумевает, что наилучшее расположение графа — это состояние с минимальным E. Расстояние dij между двумя вершинами vi и vj в графе определяется как длина кратчайшего пути между vi и vj. Алгоритм направлен на согласование длины пружины lij между частицами pi и pj с кратчайшим расстоянием пути, чтобы достичь оптимальной длины между ними на чертеже. Длина lij определяется следующим образом:
где L — желаемая длина одного ребра в области рисования. L можно определить на основе наибольшего расстояния между вершинами в графе. Если Lo — длина стороны квадрата области рисования, L можно получить следующим образом:
Сила пружины, соединяющей pi и pj, обозначается параметром kij:
Затем алгоритм КК ищет визуальное положение для каждого узла v в топологии сети и пытается уменьшить функцию энергии во всей сети. То есть алгоритм КК вычисляет частные производные для всех узлов топологии сети с точки зрения каждого xv и yv, которые равны нулю (т.е. ∂E / ∂xv = ∂E / ∂yv = 0; 1 < v < n).
Однако решение всех этих нелинейных уравнений одновременно невозможно, поскольку они зависят друг от друга. Поэтому для решения уравнения можно использовать итерационный подход, основанный на методе Ньютона-Рафсона. На каждой итерации алгоритм выбирает узел m с наибольшим максимальным изменением (Δm). Другими словами, узел m перемещается в новое положение, где он может достичь более низкого уровня Δm, чем раньше. Между тем, другие узлы остаются фиксированными. Максимальное изменение (Δm) рассчитывается следующим образом:
Алгоритм Фрухтермана-Рейнгольда основан на модели пружинного встраивания Идса. Он равномерно распределяет узлы, минимизируя пересечения ребер. Он также поддерживает одинаковую длину ребер. В отличие от алгоритма КК, он использует две силы (силы притяжения и силы отталкивания) для обновления узлов, а не использует функцию энергии с теоретическим графическим расстоянием. Во-первых, сила притяжения (fa) и сила отталкивания (fr) определяются следующим образом:
где d — расстояние между двумя узлами, а k — константа идеального попарного расстояния. Константа идеального расстояния k = √(area / n). Здесь area — область рамки чертежа, n — общее количество узлов в топологии сети.
Алгоритм Фрухтермана-Рейнгольда выполняется итеративно, и все узлы перемещаются одновременно после расчета сил для каждой итерации. Алгоритм добавляет атрибут «смещение» для контроля смещения положения узлов. В начале итерации алгоритм Фрухтермана-Рейнгольда вычисляет начальное значение смещения для всех узлов с использованием силы отталкивания (fr). Алгоритм также использует силу притяжения (fa) для многократного обновления визуального положения узлов на каждом ребре. Наконец, он обновляет смещение положения узлов, используя значение смещения.
Это реализация двух алгоритмов: Камада-Каваи и Фрухтермана-Рейнгольда на языке программирования Си. Структура Graph включает в себя два динамических массива: один массив указателей на вершины и один массив ребер c их размерами.
struct Graph
{
struct Vertex **vertexes;
struct Edge *edges;
int vertexes_num;
int edges_num;
};Каждая вершина имеет имя и свое местоположение в векторной форме:
struct Vertex { int name; struct Vector location; };Ребро состоит из двух указателей на вершины, которые оно соединяет:
struct Edge { struct Vertex *start; struct Vertex *end; };void ForceDirectedLayout(struct Graph *graph, int max_iteration)
{
int v_num = graph->vertexes_num;
double k = sqrt(LENGTH * LENGTH / v_num);
double t = 20;
int stop_count = 0;
// Stop when total movement falls under a certain range
// for (int i = 0; i < max_iteration; i++)
while (stop_count < max_iteration)
{
struct Vector displacement[v_num];
// Calculate the repulsive forces on vertexes/electrons
for (int i = 0; i < v_num; i++)
{
displacement[i] = new_vector(0, 0);
for (int j = 0; j < v_num; j++)
{
if (i != j)
{
struct Vector diff = sub(graph->vertexes[i]->location, graph->vertexes[j]->location);
// displacement = displacement + (diff / |diff|) * Fr
displacement[i] = add(displacement[i], multiply(devide(diff, absolute(diff)), Fr(absolute(diff), k)));
}
}
}
// Calculate the attractive forces on edges/springs
for (int i = 0; i < graph->edges_num; i++)
{
int start_i = findVIndex(graph->edges[i].start, graph);
int end_i = findVIndex(graph->edges[i].end, graph);
struct Vector diff = sub(graph->vertexes[start_i]->location, graph->vertexes[end_i]->location);
// displacement = displacement +- (diff / |diff|) * Fa
displacement[start_i] = sub(displacement[start_i], multiply(devide(diff, absolute(diff)), Fa(absolute(diff), k)));
displacement[end_i] = add(displacement[end_i], multiply(devide(diff, absolute(diff)), Fa(absolute(diff), k)));
}
double total_displacement = 0;
// Limit the max displacement to a temperature t and keep them inside the frame
// The temperature t allows for large movements at the beginning of the loop
// and smaller, more refined movements near the end.
for (int i = 0; i < v_num; i++)
{
struct Vector disp = displacement[i];
struct Vector lim_disp = multiply(devide(disp, absolute(disp)), __min(absolute(disp), t));
graph->vertexes[i]->location = add(graph->vertexes[i]->location, lim_disp);
total_displacement += absolute(lim_disp);
}
// Stop when total movement falls under a certain range
if (total_displacement < 0.0001 * (v_num))
{
printf("Small displacement\n");
stop_count++;
}
t = cool(t);
}
printf("Graph placed with force-directed layout!\n");
}
void LocalMinimum(struct Graph *gr, double eps)
{
// Two dimensional array of shortest path between two vertexes
// Calculate using Floyd-Warshall algorithm
int **d = floyd_warshall(*gr);
int v_num = gr->vertexes_num;
int e_num = gr->edges_num;
double Lo = LENGTH * 10 / e_num;
double K = 100;
int d_max = d[0][0];
for (int i = 0; i < v_num; i++)
{
for (int j = i + 1; j < v_num; j++)
{
d_max = __max(d_max, d[i][j]);
}
}
// Initializing l_ij, k_ij
double **l = (double **)malloc(sizeof(double *) * v_num);
double **k = (double **)malloc(sizeof(double *) * v_num);
for (int i = 0; i < v_num; i++)
{
l[i] = (double *)malloc(sizeof(double) * v_num);
k[i] = (double *)malloc(sizeof(double) * v_num);
for (int j = 0; j < v_num; j++)
{
l[i][j] = Lo / d_max * d[i][j];
k[i][j] = K / pow(d[i][j], 2);
}
}
// Moving the vertex with highest energy decrease
double *Delta = (double *)malloc(sizeof(double) * v_num);
int max_i = calcDelta(gr, k, l, Delta);
while (Delta[max_i] > eps)
{
while (Delta[max_i] > eps)
{
struct Vector dE = new_vector(0, 0);
double Exx = 0;
double Exy = 0;
double Eyy = 0;
for (int i = 0; i < v_num; i++)
{
if (i == max_i)
continue;
struct Vector dmax_i = sub(gr->vertexes[max_i]->location, gr->vertexes[i]->location);
double n = 1.0 - l[max_i][i] / absolute(dmax_i);
dE = add(dE, multiply(multiply(dmax_i, n), k[max_i][i]));
Exy += k[max_i][i] * l[max_i][i] * dmax_i.x * dmax_i.y / pow(absolute(dmax_i), 3);
Exx += k[max_i][i] * (1.0 - l[max_i][i] * dmax_i.y * dmax_i.y / pow(absolute(dmax_i), 3));
Eyy += k[max_i][i] * (1.0 - l[max_i][i] * dmax_i.x * dmax_i.x / pow(absolute(dmax_i), 3));
}
double D = Exx * Eyy - Exy * Exy;
struct Vector d;
d.x = -(Eyy * dE.x - Exy * dE.y) / D;
d.y = -(-Exy * dE.x + Exx * dE.y) / D;
gr->vertexes[max_i]->location = add(gr->vertexes[max_i]->location, d);
Delta[max_i] = absolute(dE);
}
max_i = calcDelta(gr, k, l, Delta);
}
printf("Graph placed with local minimum layout!\n");
}
int calcDelta(struct Graph gr, double **k, double **l, double *Delta)
{
double maxDelta = 0;
int m_i = 0;
for (int i = 0; i < gr.vertexes_num; i++)
{
// dE is vector energy
struct Vector dE = new_vector(0, 0);
for (int j = 0; j < gr.vertexes_num; j++)
{
if (i == j)
continue;
struct Vector d = sub(gr.vertexes[i]->location, gr.vertexes[j]->location);
double n = 1.0 - l[i][j] / absolute(d);
dE = add(dE, multiply(multiply(d, n), k[i][j]));
}
// Find vertex with highest energy
Delta[i] = absolute(dE);
if (Delta[i] > maxDelta)
{
maxDelta = Delta[i];
m_i = i;
}
}
return m_i;
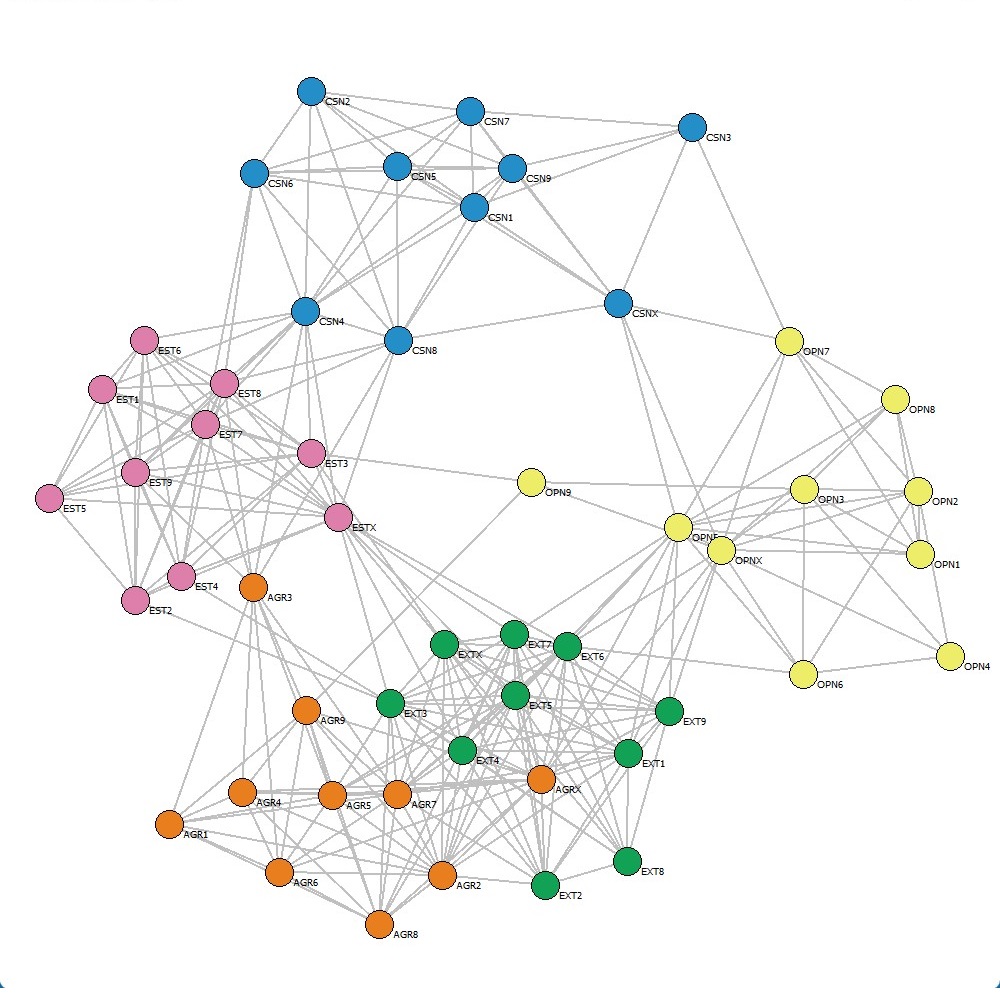
}Раскладка графа Local minmum - Kamada - Kawaii
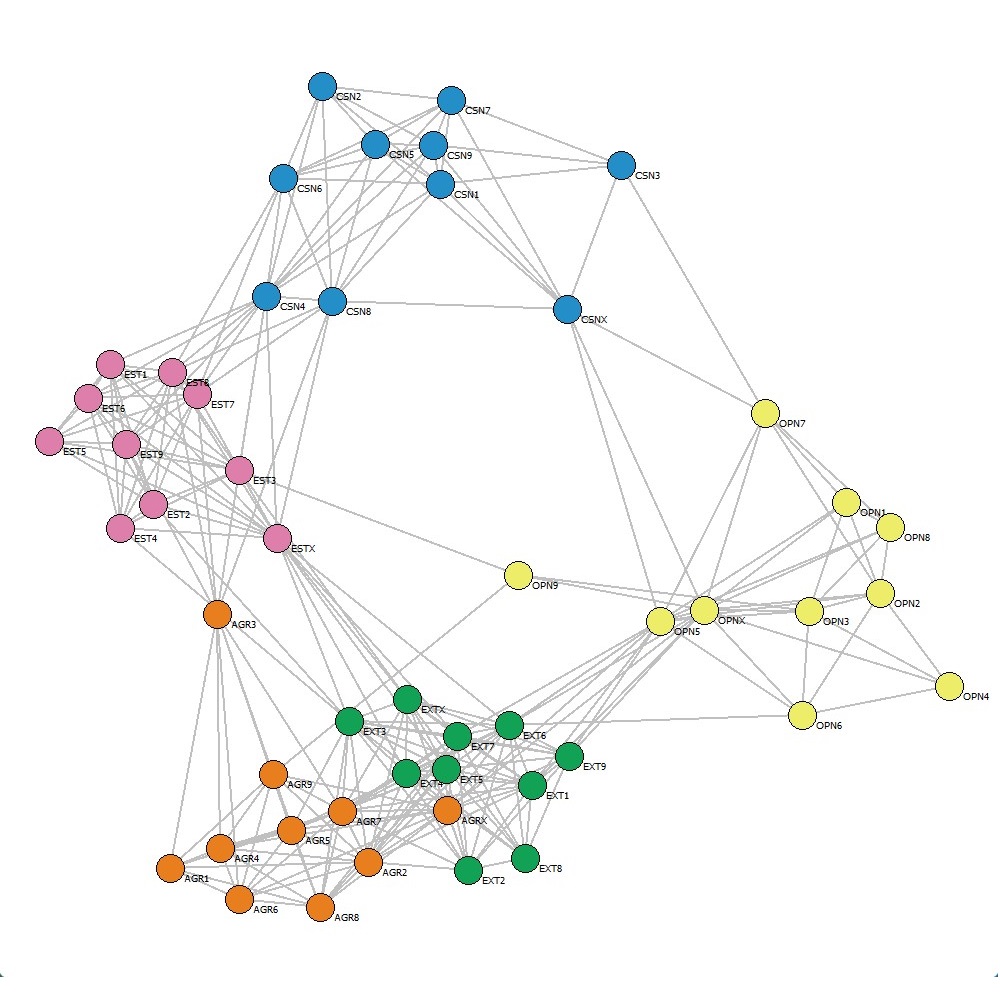
Раскладка графа Force-directed layout - Fruchterman - Reingold