Skip to content

Latest commit

 

History

History
379 lines (331 loc) · 9.16 KB

README.md

File metadata and controls

379 lines (331 loc) · 9.16 KB
Raw

2368. 受限条件下可到达节点的数目

English Version

题目描述

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目。

注意，节点 0 不 会标记为受限节点。

 

示例 1：

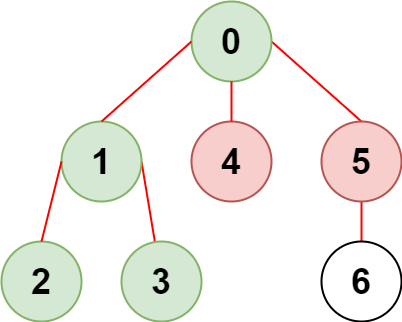
输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出：4
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。

示例 2：

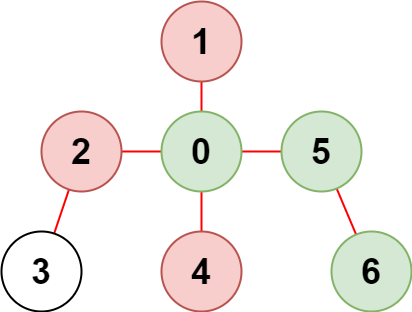
输入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
输出：3
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,5,6] 可以从节点 0 到达。

 

提示：

  • 2 <= n <= 105
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • edges 表示一棵有效的树
  • 1 <= restricted.length < n
  • 1 <= restricted[i] < n
  • restricted 中的所有值 互不相同

解法

方法一：DFS/BFS

建图，利用哈希表 $vis$ 记录有哪些受限的节点，然后 $DFS$ 或者 $BFS$ 搜索整个图，记录访问过的节点数目。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。

Python3

class Solution:
    def reachableNodes(
        self, n: int, edges: List[List[int]], restricted: List[int]
    ) -> int:
        g = defaultdict(list)
        vis = [False] * n
        for v in restricted:
            vis[v] = True
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)

        def dfs(u):
            nonlocal ans
            if vis[u]:
                return
            ans += 1
            vis[u] = True
            for v in g[u]:
                dfs(v)

        ans = 0
        dfs(0)
        return ans
class Solution:
    def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:
        s = set(restricted)
        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        q = deque([0])
        vis = [False] * n
        for v in restricted:
            vis[v] = True
        ans = 0
        while q:
            i = q.popleft()
            ans += 1
            vis[i] = True
            for j in g[i]:
                if not vis[j]:
                    q.append(j)
        return ans

Java

class Solution {
    private List<Integer>[] g;
    private boolean[] vis;
    private int ans;

    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        g = new List[n];
        for (int i = 0; i < n; ++i) {
            g[i] = new ArrayList<>();
        }
        vis = new boolean[n];
        for (int v : restricted) {
            vis[v] = true;
        }
        for (int[] e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }

        ans = 0;
        dfs(0);
        return ans;
    }

    private void dfs(int u) {
        if (vis[u]) {
            return;
        }
        ++ans;
        vis[u] = true;
        for (int v : g[u]) {
            dfs(v);
        }
    }
}
class Solution {
    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        List<Integer>[] g = new List[n];
        for (int i = 0; i < n; ++i) {
            g[i] = new ArrayList<>();
        }
        for (int[] e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        boolean[] vis = new boolean[n];
        for (int v : restricted) {
            vis[v] = true;
        }
        Deque<Integer> q = new ArrayDeque<>();
        q.offer(0);
        int ans = 0;
        while (!q.isEmpty()) {
            int i = q.pollFirst();
            ++ans;
            vis[i] = true;
            for (int j : g[i]) {
                if (!vis[j]) {
                    q.offer(j);
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int ans;

    int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        vector<bool> vis(n);
        for (int v : restricted) vis[v] = true;
        ans = 0;
        dfs(0, g, vis);
        return ans;
    }

    void dfs(int u, vector<vector<int>>& g, vector<bool>& vis) {
        if (vis[u]) return;
        vis[u] = true;
        ++ans;
        for (int v : g[u]) dfs(v, g, vis);
    }
};
class Solution {
public:
    int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
        vector<vector<int>> g(n);
        vector<bool> vis(n);
        for (auto& e : edges)
        {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        for (int v : restricted) vis[v] = true;
        queue<int> q{{0}};
        int ans = 0;
        while (!q.empty())
        {
            int i = q.front();
            q.pop();
            ++ans;
            vis[i] = true;
            for (int j : g[i]) if (!vis[j]) q.push(j);
        }
        return ans;
    }
};

Go

func reachableNodes(n int, edges [][]int, restricted []int) int {
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	vis := make([]bool, n)
	for _, v := range restricted {
		vis[v] = true
	}
	ans := 0
	var dfs func(u int)
	dfs = func(u int) {
		if vis[u] {
			return
		}
		vis[u] = true
		ans++
		for _, v := range g[u] {
			dfs(v)
		}
	}
	dfs(0)
	return ans
}
func reachableNodes(n int, edges [][]int, restricted []int) int {
	g := make([][]int, n)
	vis := make([]bool, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	for _, v := range restricted {
		vis[v] = true
	}
	q := []int{0}
	ans := 0
	for len(q) > 0 {
		i := q[0]
		q = q[1:]
		ans++
		vis[i] = true
		for _, j := range g[i] {
			if !vis[j] {
				q = append(q, j)
			}
		}
	}
	return ans
}

TypeScript

function reachableNodes(
    n: number,
    edges: number[][],
    restricted: number[],
): number {
    let res = 0;
    const vis = new Array(n).fill(false);
    const map = new Map<number, number[]>();
    for (const [start, end] of edges) {
        map.set(start, [...(map.get(start) ?? []), end]);
        map.set(end, [...(map.get(end) ?? []), start]);
    }
    const dfs = (cur: number) => {
        if (restricted.includes(cur) || vis[cur]) {
            return;
        }
        res++;
        vis[cur] = true;
        for (const item of map.get(cur) ?? []) {
            dfs(item);
        }
    };
    dfs(0);

    return res;
}
function reachableNodes(
    n: number,
    edges: number[][],
    restricted: number[],
): number {
    const g = Array.from({ length: n }, () => []);
    const vis = new Array(n).fill(false);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    for (const v of restricted) {
        vis[v] = true;
    }
    const q = [0];
    let ans = 0;
    while (q.length) {
        const i = q.shift();
        ++ans;
        vis[i] = true;
        for (const j of g[i]) {
            if (!vis[j]) {
                q.push(j);
            }
        }
    }
    return ans;
}

...