Skip to content

Commit

Permalink
Add livebook
Browse files Browse the repository at this point in the history
  • Loading branch information
@msluszniak
msluszniak committed May 7, 2024
1 parent 9a931aa commit 2431ff2
Showing 1 changed file with 255 additions and 0 deletions.
255 changes: 255 additions & 0 deletions notebooks/nearest_neighbors.livemd
View file
Original file line number Diff line number Diff line change
@@ -0,0 +1,255 @@
<!-- livebook:{"file_entries":[{"name":"knn_gyms.png","type":"attachment"}]} -->

# Nearest Neighbors

```elixir
Mix.install([
{:scholar, path: "/home/mateusz/Dashbit/scholar", override: true},
{:explorer, "~> 0.8.1"},
{:exla, "~> 0.7.2"},
{:nx, "~> 0.7.2"},
{:req, "~> 0.4.14"},
{:kino_vega_lite, "~> 0.1.11"},
{:kino, "~> 0.12.3"},
{:kino_explorer, "~> 0.1.18"}
])
```

## Setup

```elixir
require Explorer.DataFrame, as: DF
require Explorer.Series, as: S
Nx.global_default_backend(EXLA.Backend)
```

## Introduction to Nearest Neighbors

In this notebook, we introduce the concept of "**nearest neighbors**." We start by defining what nearest neighbors are and why they are useful in real-life scenarios. Next, we present various methods to compute them, highlighting the advantages and disadvantages of each approach. To make this notebook easier to follow, we will demonstrate these algorithms on a few examples and analyze the results.

## Definition of K-Nearest Neighbors

Let's first define what exactly "nearest neighbors" are. Consider a set of points ${p_1, p_2, \ldots, p_N}$, where each point $p_i$ is represented as a vector of size $M$, with real-number coordinates: $p_i = (p_{i1}, p_{i2}, \ldots, p_{iM})$. We say that the dimension of the space is $M$. For convenience, instead of listing the set of points as ${p_1, p_2, \ldots, p_N}$, we can treat it as a matrix $P$ of size $N \times M$, where $P_{ij}$ represents the $j$th coordinate of the $i$th point.

A metric between two points $a$ and $b$ is defined as a function d that takes two points and returns a non-negative real number, subject to the following conditions for arbitrary points $a$, $b$, and $c$:

* $d(a,b) = 0 \iff a = b$ (identity)
* $d(a,b) = d(b, a)$ (symmetry)
* $d(a,b) \leq d(a, c) + d(b, c)$ (triangle inequality)

Examples of such metrics include the Euclidean metric and the Manhattan metric.

Given a set of points $P$, a point $q$, and a metric $d$, the $k$ nearest neighbors from $P$ to point $q$ are defined as a set $S \subseteq P$, with $\lvert S \rvert = k$, where the distance $d$ between the points in $S$ and $q$ is minimized. In simpler terms, $S$ is a set of $k$ points from $P$ with the smallest distance to point $q$.

It's especially interesting to consider the case when point $q$ is part of the set $P$. In the remainder of the notebook, we will assume that $q$ is indeed in $P$, and if this is not the case, we will note it explicitly.

## Why Do We Want to Use K-Nearest Neighbors

Now, after the formal section with definitions, let's move on to the more practical part: why would we even want to calculate something like K-nearest Neighbors? Consider the following example. Let's say you've just moved to a new city, and you're here for the first time. Since you're an active person, you'd like to find a nearby gym with good facilities. What would you do? You'd probably start by searching for gyms on online maps. The search results might look something like this.

<!-- livebook:{"break_markdown":true} -->

![](files/knn_gyms.png)

<!-- livebook:{"break_markdown":true} -->

Now you can check out the gyms and eventually decide which one will be your regular spot. What did the search engine do? It basically calculated the nearest gyms (nearest neighbors) from your current location, which is the essence of finding nearest neighbors.

Now let's move to a more abstract example. You're listening to your favorite rock playlist and you think, "Yeah, these tracks are cool, but I've been listening to them on repeat. Maybe I should explore some new music." Searching for random songs might not be the most effective approach; you could end up with hip-hop or pop tracks, which you may not enjoy as much. However, it might also lead you to discover entirely new genres. A better approach could be to explore other rock playlists available online. While these playlists align with your preferred genre, they may not consider your unique tastes within rock music. Wouldn't it be great if there were a tool that could recommend new songs based on your previous playlists? Fortunately, such tools exist!

One type of [recommendation system](https://en.wikipedia.org/wiki/Recommender_system) relies on collaborative filtering: it recommends songs based on what other users with similar musical tastes listen to. Another approach is to treat songs as points, like in our earlier definition, and then compute the closest songs to your favorites. This is another example of calculating nearest neighbors. While it might not be immediately obvious how to represent songs as points and measure the "distance" between them, it turns out that it can be done.

Another use of nearest neighbors is in building classifiers and regressors. This approach was covered in a [previous notebook](https://github.com/elixir-nx/scholar/blob/main/notebooks/k_nearest_neighbors.livemd), which we strongly recommend you review before proceeding with this one.

## How to compute K-Nearest Neighbors - Brute Force Approach

Now let's consider how we can compute the $k$-nearest neighbors. The simplest method is to compute the distance using a metric $d$ for each pair of points in the dataset. This can be represented as a matrix $D$ of size $N \times N$, where $D_{ij}$ indicates the distance between the $i$th and $j$th points. Given the symmetry of metric $d$, the matrix $D$ is also symmetric: $D_{ij} = D_{ji}$. To find the nearest neighbors, you would sort the distances for each point (sorting the rows of matrix $D$), and then return only the first $k$ columns from each row of the sorted matrix.

While this method accurately computes the $k$-nearest neighbors, it has a major drawback: time complexity. The time complexity of this approach is $O(MN^2 + N\log(N)) = O(MN^2)$, where $N$ is the number of points, and $M$ represents the number of dimensions (features) of each point. Even if we set $M = 1$, when $N$ is very large (like the number of songs on Spotify, which is on the order of $10^8$), the number of operations required becomes unfeasible, even if $k$ is relatively small.

Given this, for large values of $N$, we need to consider other approaches. However, the brute-force method can still be useful in certain situations. If $N$ is small, the distance matrix $D$ can be computed in a reasonable amount of time. Additionally, if $k \approx N$, this approach is optimal since you always need to compute $O(Nk)$, which leads to $O(N^2)$ operations. Computing the distance matrix is optimized in many frameworks, giving it an advantage over other methods when $k$ is on the order of magnitude of $N$.

In Scholar, the brute-force approach is implemented [here](https://github.com/elixir-nx/scholar/blob/main/lib/scholar/neighbors/k_nearest_neighbors.ex). In a previous section, we mentioned a notebook that uses this approach to calculate $k$-nearest neighbors.

<!-- livebook:{"branch_parent_index":3} -->

## How to compute K-Nearest Neighbors - KDtrees

From the previous section, we know that for large datasets, we need a much faster approach. It turns out that there is a data structure that allows querying for a single neighbor in $O(\log(N))$ average time, resulting in a total computation time of $O(kN\log(N))$, which is efficient for small values of $k$. But what is this data structure that allows querying faster than the brute-force approach? It's called a **KDTree**. KDTree, short for "K-Dimensional Tree", is a tree structure that organizes points in a K-dimensional space. More precisely, it's a binary tree where each non-leaf node has an associated splitting hyperplane. All points on the left side of this splitting hyperplane belong to the left subtree, while those on the right side belong to the right subtree. The dimension along which the split occurs is consistent across each level of the tree, and it changes as you move to different levels.

To better understand this, let's look at two graphical examples of KDTrees.

<!-- livebook:{"break_markdown":true} -->

| ![KDTree](https://upload.wikimedia.org/wikipedia/commons/b/b6/3dtree.png) |
| :-----------------------------------------------------------------------: |

Figure 1: A 3-dimensional KDtree.

<!-- livebook:{"break_markdown":true} -->

Here, the first split (a red vertical plane) divides the root cell (white) into two subcells. Then, each of these subcells is further split (by the green horizontal planes) into two additional subcells. Finally, the four resulting subcells are further split (by four blue vertical planes), creating a total of eight subcells. Since there are no more sectors to split, the algorithm terminates with these eight subcells.

Here's another, more abstract example.

| ![KDtree](https://upload.wikimedia.org/wikipedia/commons/4/4f/Kd-tree-example-with_records_as_leaf_nodes.png) |
| :-----------------------------------------------------------------------------------------------------------: |

Figure 2: A different example of 3-dimensional KDtree.

<!-- livebook:{"break_markdown":true} -->

In this example, the dimensions are abstract values like name, salary, and age. However, because we can define a linear order for each feature (such as a natural order for salary and age, and a lexicographic order for names), we can treat them like any other metric space.

Now, let's move on to the code and implementation of KDTrees in Scholar!

<!-- livebook:{"branch_parent_index":3} -->

## KDtrees in action - Practical Example

In this example, we'll use data from the [National Health and Nutrition Examination Survey (NHANES) 2013-2014](https://archive.ics.uci.edu/dataset/887/national+health+and+nutrition+health+survey+2013-2014+(nhanes)+age+prediction+subset). The dataset consists of 7 features that are biomedical indicators. For more information, click the link above.

Now, let's read the data into an Explorer dataframe.

```elixir
digits_url =
"https://archive.ics.uci.edu/static/public/887/national+health+and+nutrition+health+survey+2013-2014+(nhanes)+age+prediction+subset.zip"

data =
Req.get!(digits_url).body

{:ok, [{_, data}]} = :zip.extract(data, [:memory])
df_data = DF.load_csv!(data)
```

In this analysis, we want to determine if the most similar people, in terms of medical parameters, belong to the same age group. In the dataset, we categorize people into two groups: adults (18-64 years) and seniors (65+ years). Intuitively, we might expect that people with similar medical results are often in the same age group, but we want to quantify the extent to which this is true. To do this, we compute the 5 closest results for each patient and then calculate the average for these two groups.

First, we need to separate the medical results from the data that indicates the age group.

```elixir
x = df_data |> DF.discard(["age_group", "SEQN", "RIDAGEYR"]) |> Nx.stack(axis: 1)
y = Nx.stack(S.cast(df_data["age_group"], :category), axis: 1)

x = Scholar.Preprocessing.StandardScaler.fit_transform(x)

{x, y}
```

Once the data is preprocessed, we can move on to the KDTree model. First, we need to set up the model using `Scholar.Neighbors.KDTree.fit`. This method initializes the tree structure for further processing.

```elixir
num_neighbors = 6

knn_model =
EXLA.jit_apply(&Scholar.Neighbors.KDTree.fit(&1, k: num_neighbors, metric: :euclidean), [x])
```

Now, we need to run a query to calculate the nearest neighbors for a given set of data. To compute the nearest neighbors, we call `Scholar.Neighbors.KDTree.predict`.

```elixir
knn =
EXLA.jit_apply(
&Scholar.Neighbors.KDTree.predict(&1, &2, k: num_neighbors, metric: {:minkowski, 2}),
[
knn_model,
x
]
)
```

Before we compute the statistics from the results, we need to now what are the proportions of each group initially.

```elixir
seniors_original = Nx.divide(Nx.sum(Nx.equal(y, 1)), Nx.size(y))
adults_original = Nx.subtract(1, seniors_original)
{seniors_original, adults_original}
```

As we can see, about 16% of the people are seniors, while 84% are adults. Now, let's calculate the average number of people within the same age group among the nearest neighbors. We should drop the first column since we're not interested in considering the point itself when calculating its neighborhood.

```elixir
knn = knn[[.., 1..-1//1]]
age_groups = Nx.take(y, knn)

seniors =
Nx.divide(
Nx.sum(Nx.multiply(Nx.equal(age_groups, 1), Nx.new_axis(Nx.equal(y, 1), 1))),
Nx.sum(Nx.equal(y, 1))
)
|> Nx.divide(num_neighbors - 1)

adults =
Nx.divide(
Nx.sum(Nx.multiply(Nx.equal(age_groups, 0), Nx.new_axis(Nx.equal(y, 0), 1))),
Nx.sum(Nx.equal(y, 0))
)
|> Nx.divide(num_neighbors - 1)

{seniors, adults}
```

Our intuition was correct: for seniors, 28% of their nearest neighbors in terms of medical results are also seniors, while for adults, nearly 86% of their nearest neighbors are also adults. This indicates that age should always be considered to ensure proper treatment when assessing medical results and drawing conclusions.

## How to compute Approximated Nearest Neighbors - LargeVis

In the previous example, KDTree was a perfect choice for computing K-Nearest Neighbors. However, this approach doesn't always work effectively. When the number of features grows, the efficiency of KDTree decreases significantly, so it's best suited for data with a smaller number of features (<15), like in the previous example. For data with many samples but also many features, a different approach is required. Here, algorithms that return an approximated version of nearest neighbors are needed. These approximated algorithms may not give exact solutions, but the deviation is usually minor and accepted as a tradeoff for faster computation. An example of an algorithm that computes approximated nearest neighbors is LargeVis.

LargeVis is an approximated nearest neighbors algorithm that uses the concept of a Random Projection Forest. A Random Projection Forest consists of multiple trees. Each tree is built using a divide-and-conquer approach. The entire dataset is used to start the construction, and at each node, the data is projected onto a random hyperplane and split as follows: points with a projection smaller than or equal to the median go into the left subtree, while those with a projection greater than the median go into the right subtree. This process is then recursively applied to the left and right subtrees.

This structure allows us to quickly create an approximated nearest neighbors graph, which can then be used to find the nearest neighbors efficiently. To better understand this, below is a figure illustrating the process of creating a tree in a random projection forest.

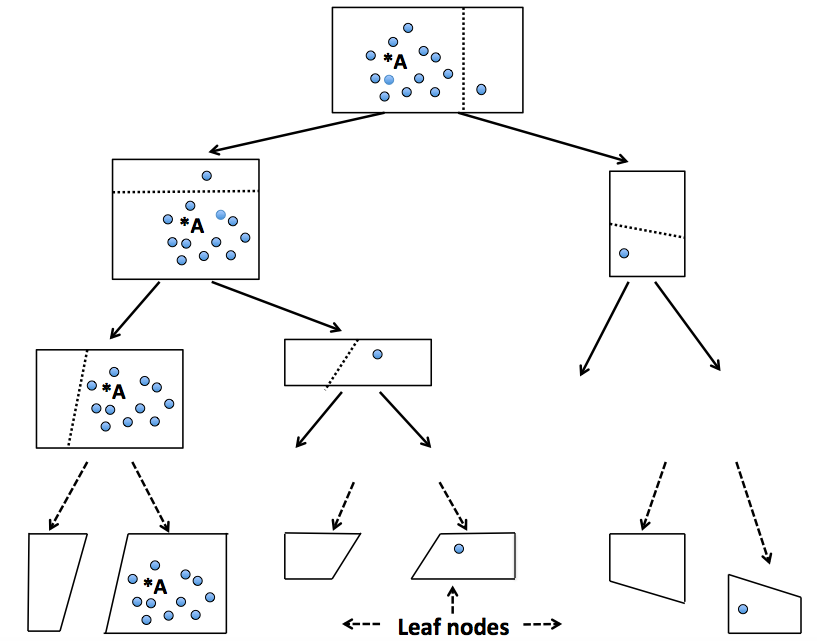| ![Random Projection Forest](http://www.math.umassd.edu/~dyan/rpKNN.png?attredirects=0) |
| :------------------------------------------------------------------------------------: |

Figure 3: A process of creating a tree in Random Projection Forest. Source: http://www.math.umassd.edu/~dyan/rpKNN.png?attredirects=0

<!-- livebook:{"break_markdown":true} -->

Here's a brief explanation of LargeVis. First, we compute an approximated nearest neighbors graph using a Random Projection Forest. Then, we refine the graph by examining the neighbors of each point's neighbors for a fixed number of iterations. Now, let's use LargeVis in practice.

In this example, we will use a dataset on online news popularity. This dataset summarizes a diverse set of features about articles published by Mashable over a two-year period. To read more about this dataset, click [here](https://archive.ics.uci.edu/dataset/332/online+news+popularity). Usually, the dataset is used to predict the number of shares on social networks, but we'll use it differently. KNN and Approximated Nearest Neighbors can be valuable in data mining, particularly in business scenarios. Imagine you're an editor at an online news agency, and you want to create a series of articles that boost your reach. One strategy could be to examine groups of the most popular articles and analyze them to identify specific patterns. We can use Approximated Nearest Neighbors to do this. For each news article, we'll calculate its nearest neighbors and then sort these groups by the total number of shares they receive on social networks.

The first step is to load the dataset from the Internet archive.

```elixir
digits_url =
"https://archive.ics.uci.edu/static/public/332/online+news+popularity.zip"

raw_data =
Req.get!(digits_url).body
```

Next, we load the data into a dataframe.

```elixir
{:ok, [_, {_, data}]} = :zip.extract(raw_data, [:memory])
data = String.replace(data, ", ", ",")
df_data = DF.load_csv!(data, delimiter: ",")
```

Next, we split the data into two parts: the target variable (shares, or $y$) and the rest of the data ($x$). We separate the shares from $x$ to avoid introducing bias. We also remove URLs because tensors do not support non-numerical data types, and we exclude the timedelta feature, which is an auxiliary feature used in creating the dataset. Finally, we apply standard scaling to $x$.

```elixir
x = df_data |> DF.discard(["url", "timedelta", "shares"]) |> Nx.stack(axis: 1)
y = Nx.stack(df_data[["shares"]], axis: 1)

x = Scholar.Preprocessing.StandardScaler.fit_transform(x)
{x, y}
```

Now, let's move on to computing the approximated nearest neighbors. Notice that this dataset has significantly more features than the previous one (58 compared to 7).

```elixir
num_neighbors = 6
{indices, _dist} = Scholar.Neighbors.LargeVis.fit(x, num_neighbors: num_neighbors)
```

Finally, we compute the nearest neighbors and sort them in descending order based on the sum of shares.

```elixir
shares_of_neighbors = Nx.take(y, indices) |> Nx.squeeze(axes: [-1]) |> Nx.sum(axes: [-1])
ord = Nx.argsort(shares_of_neighbors, direction: :desc)
Nx.take(indices, ord)
```

Notice that the first six groups are quite similar. The condition that a neighbor of your neighbor is also your neighbor is often satisfied, which is why LargeVis uses this fact to refine the results of Random Projection Forests.

0 comments on commit 2431ff2

Please sign in to comment.