Booleans

true and false;

is false. You receive similarly sensible results for or, xor and not, as well as the more esoteric nand, nor and xnor, and comparison operators return boolean values:

10 < 12 and 12 < 14; // true

Evaluation of the binary boolean operators is short circuited appropriately so true or something will not evaluate something. The exceptions are xor and xnor which must evaluate both their arguments.

Comparison Operators

The standard comparison operators are available. They require that the types of their arguments agree, and in F♮ any two data with the same type can be compared (sometimes somewhat arbitrarily, for example false < true.) The operators are:

op	name
==	equal to
!=	not equal to
<	less than
>	greater than
<=	less than or equal to
>=	greater than or equal to

Some effort has been made to allow all data to be sortable:

• When comparing user defined types they sort in the order they are declared in, for example after typedef color { red | green | blue }, red < green and green < blue.
• Functions sort (provided they have the same type signature) by their bytecode address.
• Complex numbers do not have a well defined sort order in certain edge cases so I've imposed a fairly arbitrary "tie breaking" mechanism, discussed below.

"Spaceship" Operator

Other than the true boolean comparison operators, there's also a "spaceship" binary comparison operator <=>, borrowed from Perl, which returns one of three values: lt, eq or gt. This is obviously more efficient, especially when comparing deeply nested structures, and works well with a switch statement:

switch (a <=> b) {
  (lt) { do stuff if a < b }
  (eq) { do stuf if a == b }
  (gt) { do stuff if a > b }
}

The spaceship operator implementation as you might expect is actually used by all the other comparison operators. As mentioned above this is fairly straightforward for most types, but complex numbers are points on a plane and have no well-defined linear sequence. In order to allow them to sort the algorithm is as follows:

switch(com_real(a) <=> com_real(b), com_imag(a) / 1i <=> com_imag(b) / 1i) {
    (lt, lt) { lt }
    (lt, eq) { lt }
    (lt, gt) { compare_magnitudes(a, b) }
    (eq, lt) { lt }
    (eq, eq) { eq }
    (eq, gt) { gt }
    (gt, lt) { compare_magnitudes(a, b) }
    (gt, eq) { gt }
    (gt, gt) { gt }
}

where compare_magnitudes is

switch(com_real(a) + com_imag(a) / 1i <=> com_real(b) + com_imag(b) / 1i) {
    (lt) { lt }
    (eq) { if (com_real(a) < com_real(b)) { lt } else { gt } }
    (gt) { gt }
}

A picture should help:

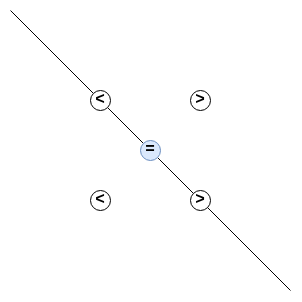
This might be crazy, but the idea is given that a != b if you draw the line y = -x + c through point a, then everything to the right of or above that line can be considered greater than a and everything to the left or below can be considered less than a. If point b is on the same line, then if b is to the left of a it is less than a else it is greater than a. This means that two numbers will sort in the same order regardless of the order they are compared (<=> remains commutative), though the left/right choice in the second condition where a and b are on the same line is arbitrary.

Next: Conditionals