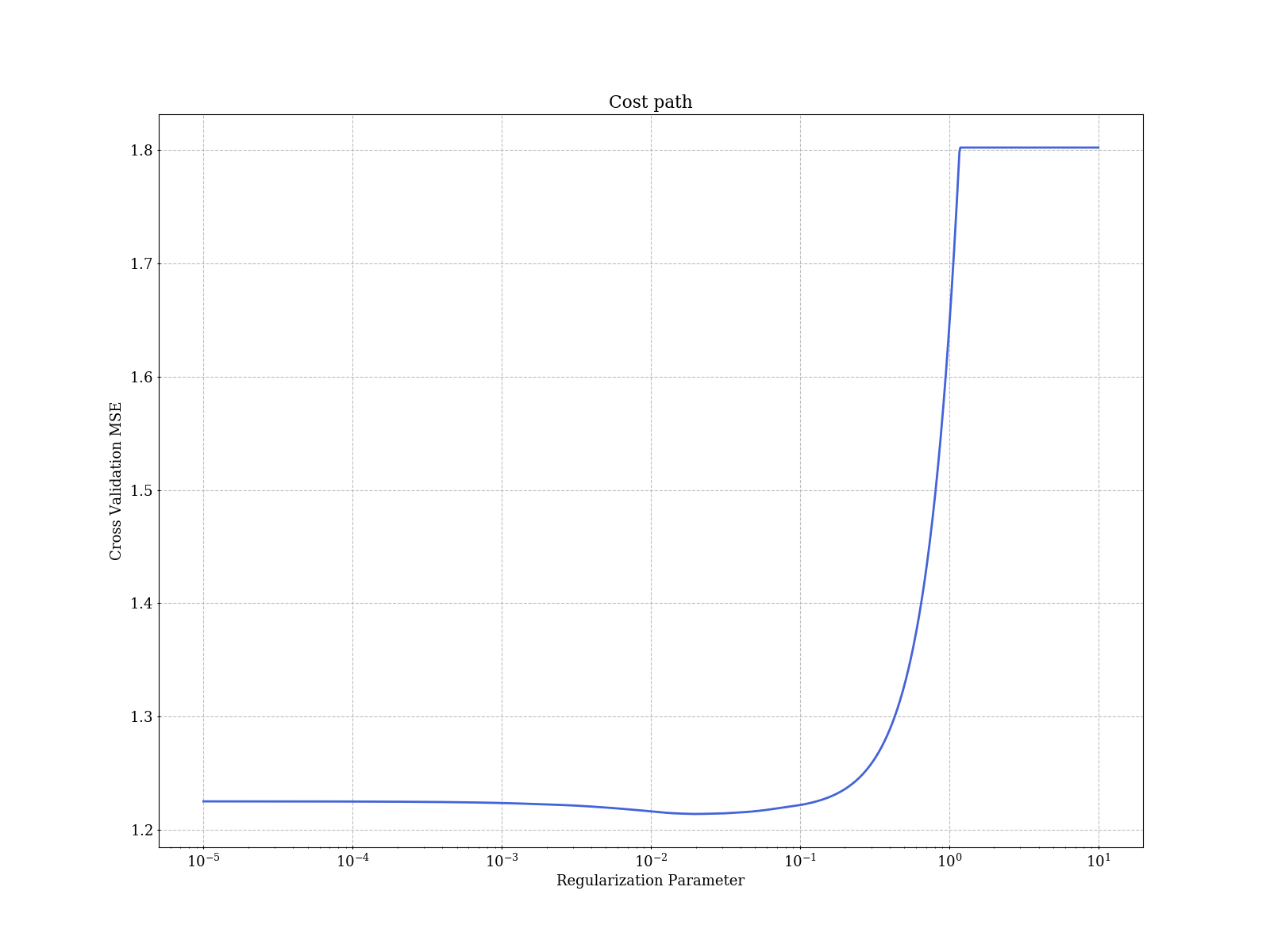
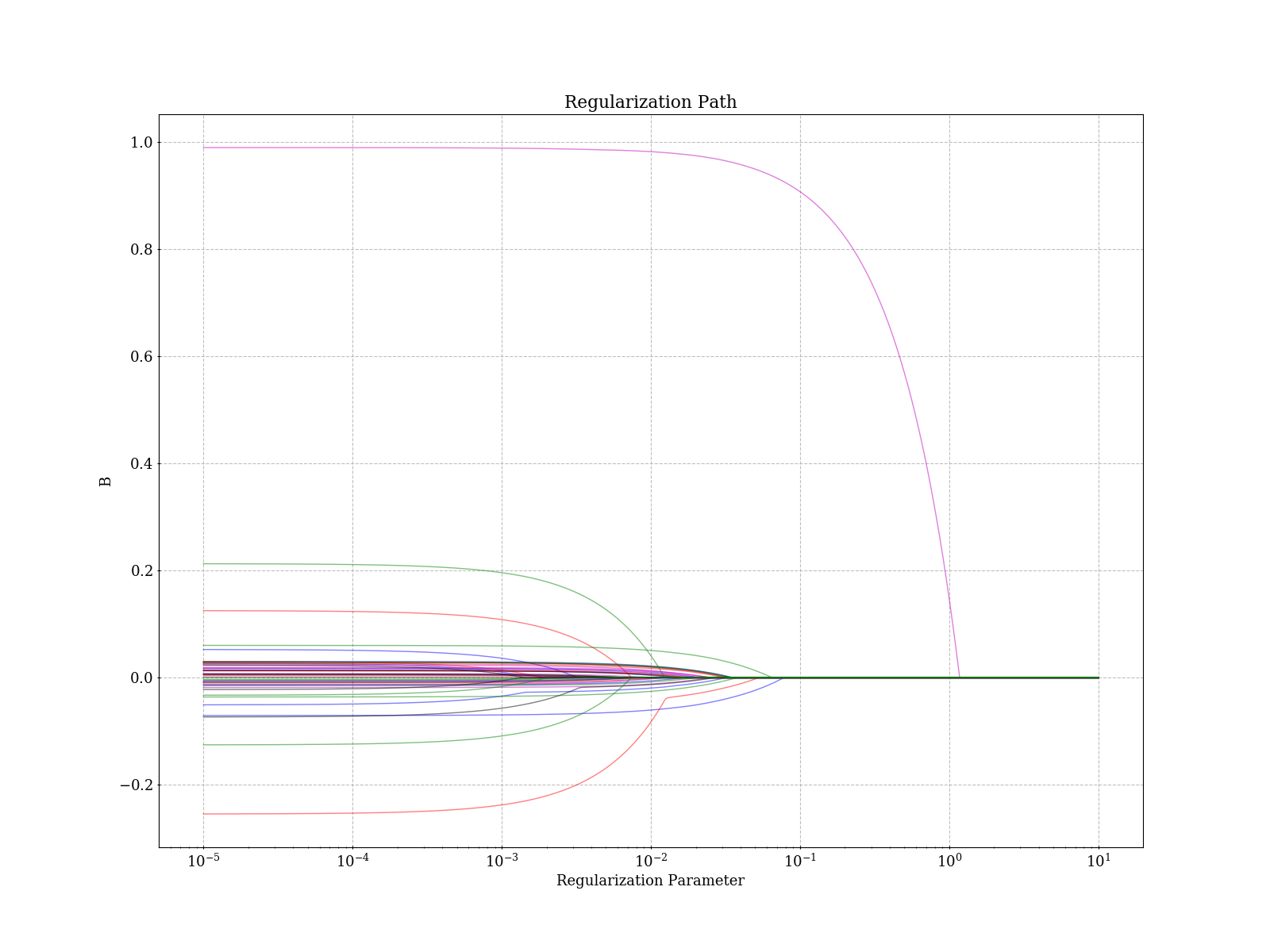
LASSO implementation (including coefficient weights) for VAR(p) models using only covariance information.

That is, we solve (roughly)

minimize_B (1/2T)sum_t||x(t) - sum_s B(s) @ x(t - s)||_2^2 + lmbda * sum_s ||vec W * B(s)||_1

using only R(s) = (1/T)sum_t x(t)x(t - s)^T, the covariance sequence. The matrix W is a weight matrix, usually set to 1 / |B_YW|^u, where B_YW is the solution with lmbda = 0.

This should be much faster than solving directly, since it takes advantage of the toeplitz structure of the covariance. Moreover, it also opens up possibilities for kernelized or other exotic estimates of the covariance R(s).

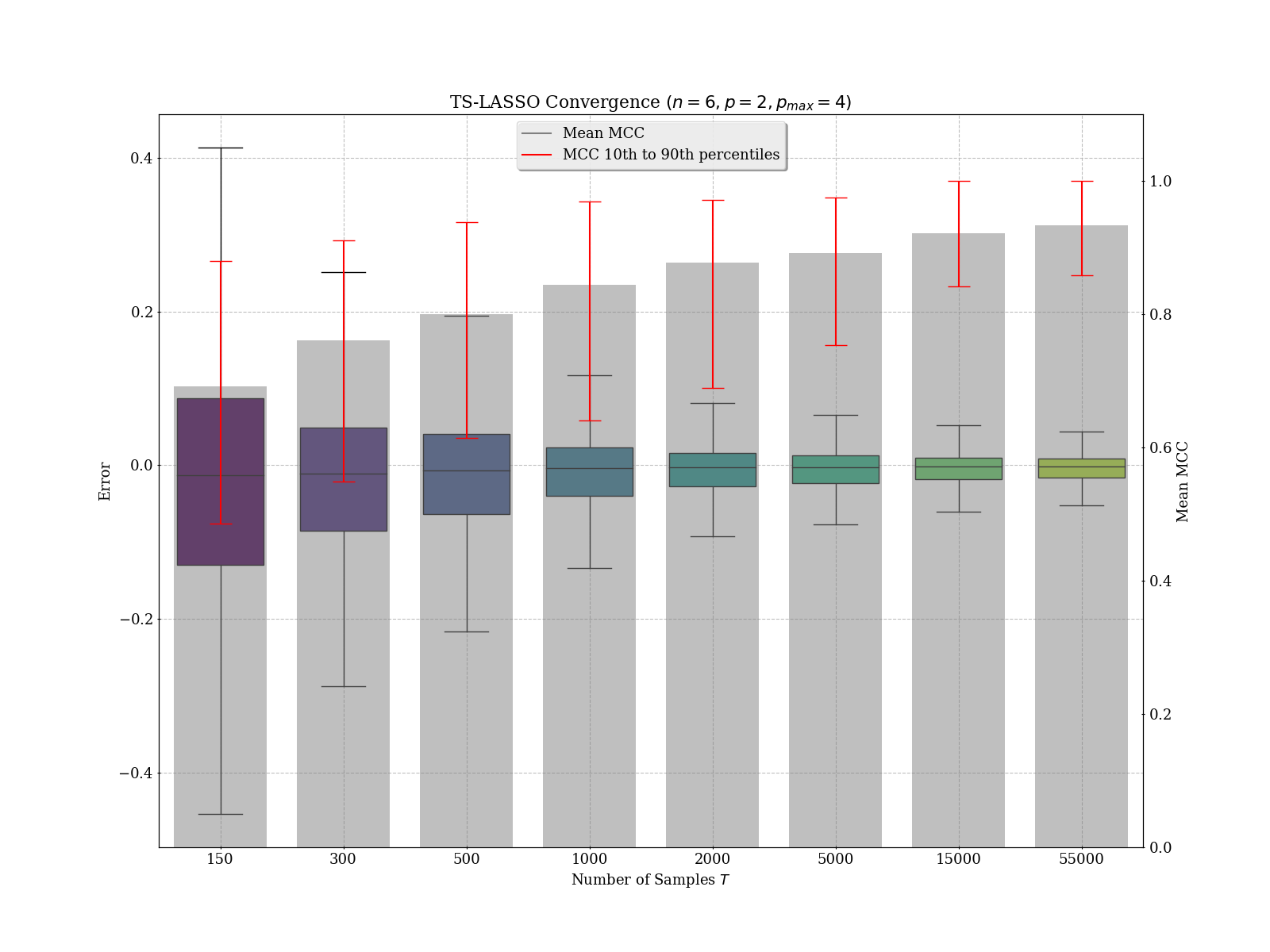
The default method is reasonably fast and reliable, at least for small systems:

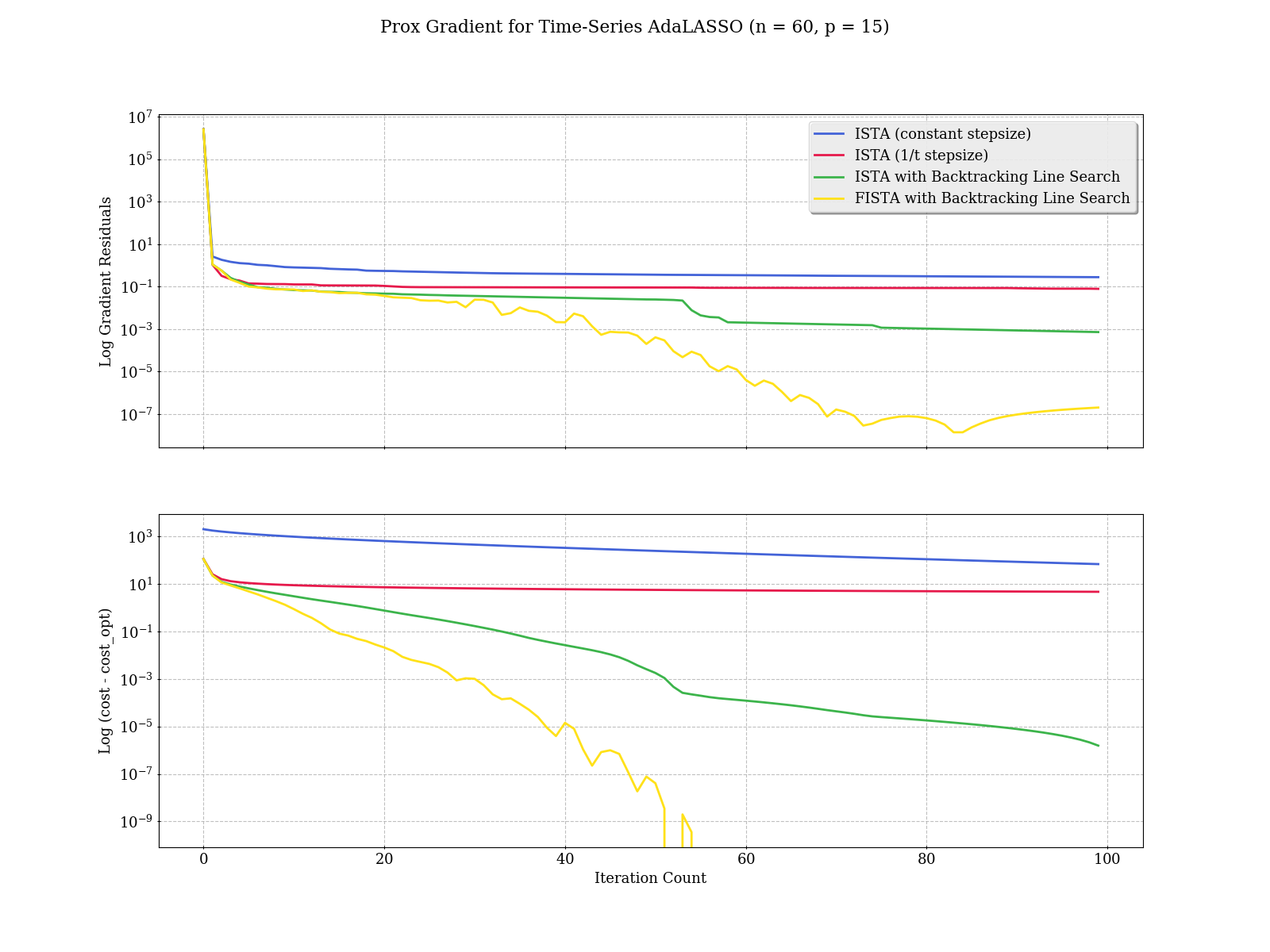
Momentum and line-search make a big difference:

Plot of the cross validation error over lambda -- the default fit_VAR method will use fminsearch to maximize the BIC.

Example regularization path: