README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Hard	https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3276.Select%20Cells%20in%20Grid%20With%20Maximum%20Score/README_EN.md	2402	Weekly Contest 413 Q3	Bit Manipulation Array Dynamic Programming Bitmask Matrix

3276. Select Cells in Grid With Maximum Score

中文文档

Description

You are given a 2D matrix grid consisting of positive integers.

You have to select one or more cells from the matrix such that the following conditions are satisfied:

• No two selected cells are in the same row of the matrix.
• The values in the set of selected cells are unique.

Your score will be the sum of the values of the selected cells.

Return the maximum score you can achieve.

 

Example 1:

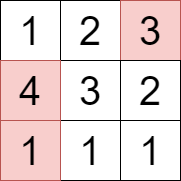
Input: grid = [[1,2,3],[4,3,2],[1,1,1]]

Output: 8

Explanation:

We can select the cells with values 1, 3, and 4 that are colored above.

Example 2:

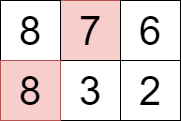
Input: grid = [[8,7,6],[8,3,2]]

Output: 15

Explanation:

We can select the cells with values 7 and 8 that are colored above.

 

Constraints:

• 1 <= grid.length, grid[i].length <= 10
• 1 <= grid[i][j] <= 100

Solutions

Solution 1: State Compression Dynamic Programming

We define $f[i][j]$ to represent the maximum score when selecting numbers from $[1,..i]$ and the state of the rows corresponding to the selected numbers is $j$. Initially, $f[i][j] = 0$, and the answer is $f[\textit{mx}][2^m - 1]$, where $\textit{mx}$ represents the maximum value in the matrix, and $m$ represents the number of rows in the matrix.

First, we preprocess the matrix using a hash table $g$ to record the set of rows corresponding to each number. Then, we can use state compression dynamic programming to solve the problem.

For the state $f[i][j]$, we can choose not to select the number $i$, in which case $f[i][j] = f[i-1][j]$. Alternatively, we can choose the number $i$. In this case, we need to enumerate each row $k$ in the set $g[i]$ corresponding to the number $i$. If the $k$-th bit of $j$ is $1$, it means we can select the number $i$. Thus, $f[i][j] = \max(f[i][j], f[i-1][j \oplus 2^k] + i)$.

Finally, we return $f[\textit{mx}][2^m - 1]$.

The time complexity is $O(m \times 2^m \times \textit{mx})$, and the space complexity is $O(\textit{mx} \times 2^m)$. Here, $m$ is the number of rows in the matrix, and $\textit{mx}$ is the maximum value in the matrix.

Python3

class Solution:
    def maxScore(self, grid: List[List[int]]) -> int:
        g = defaultdict(set)
        mx = 0
        for i, row in enumerate(grid):
            for x in row:
                g[x].add(i)
                mx = max(mx, x)
        m = len(grid)
        f = [[0] * (1 << m) for _ in range(mx + 1)]
        for i in range(1, mx + 1):
            for j in range(1 << m):
                f[i][j] = f[i - 1][j]
                for k in g[i]:
                    if j >> k & 1:
                        f[i][j] = max(f[i][j], f[i - 1][j ^ 1 << k] + i)
        return f[-1][-1]

Java

class Solution {
    public int maxScore(List<List<Integer>> grid) {
        int m = grid.size();
        int mx = 0;
        boolean[][] g = new boolean[101][m + 1];
        for (int i = 0; i < m; ++i) {
            for (int x : grid.get(i)) {
                g[x][i] = true;
                mx = Math.max(mx, x);
            }
        }
        int[][] f = new int[mx + 1][1 << m];
        for (int i = 1; i <= mx; ++i) {
            for (int j = 0; j < 1 << m; ++j) {
                f[i][j] = f[i - 1][j];
                for (int k = 0; k < m; ++k) {
                    if (g[i][k] && (j >> k & 1) == 1) {
                        f[i][j] = Math.max(f[i][j], f[i - 1][j ^ 1 << k] + i);
                    }
                }
            }
        }
        return f[mx][(1 << m) - 1];
    }
}

C++

class Solution {
public:
    int maxScore(vector<vector<int>>& grid) {
        int m = grid.size();
        int mx = 0;
        bool g[101][11]{};
        for (int i = 0; i < m; ++i) {
            for (int x : grid[i]) {
                g[x][i] = true;
                mx = max(mx, x);
            }
        }
        int f[mx + 1][1 << m];
        memset(f, 0, sizeof(f));
        for (int i = 1; i <= mx; ++i) {
            for (int j = 0; j < 1 << m; ++j) {
                f[i][j] = f[i - 1][j];
                for (int k = 0; k < m; ++k) {
                    if (g[i][k] && (j >> k & 1) == 1) {
                        f[i][j] = max(f[i][j], f[i - 1][j ^ 1 << k] + i);
                    }
                }
            }
        }
        return f[mx][(1 << m) - 1];
    }
};

Go

func maxScore(grid [][]int) int {
	m := len(grid)
	mx := 0
	g := [101][11]bool{}
	for i, row := range grid {
		for _, x := range row {
			g[x][i] = true
			mx = max(mx, x)
		}
	}
	f := make([][]int, mx+1)
	for i := range f {
		f[i] = make([]int, 1<<m)
	}
	for i := 1; i <= mx; i++ {
		for j := 0; j < 1<<m; j++ {
			f[i][j] = f[i-1][j]
			for k := 0; k < m; k++ {
				if g[i][k] && (j>>k&1) == 1 {
					f[i][j] = max(f[i][j], f[i-1][j^1<<k]+i)
				}
			}
		}
	}
	return f[mx][1<<m-1]
}

TypeScript

function maxScore(grid: number[][]): number {
    const m = grid.length;
    let mx = 0;
    const g: boolean[][] = Array.from({ length: 101 }, () => Array(m + 1).fill(false));
    for (let i = 0; i < m; ++i) {
        for (const x of grid[i]) {
            g[x][i] = true;
            mx = Math.max(mx, x);
        }
    }
    const f: number[][] = Array.from({ length: mx + 1 }, () => Array(1 << m).fill(0));
    for (let i = 1; i <= mx; ++i) {
        for (let j = 0; j < 1 << m; ++j) {
            f[i][j] = f[i - 1][j];
            for (let k = 0; k < m; ++k) {
                if (g[i][k] && ((j >> k) & 1) === 1) {
                    f[i][j] = Math.max(f[i][j], f[i - 1][j ^ (1 << k)] + i);
                }
            }
        }
    }
    return f[mx][(1 << m) - 1];
}