README.md

comments	difficulty	edit_url	rating	source	tags
true	困难	https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3276.Select%20Cells%20in%20Grid%20With%20Maximum%20Score/README.md	2402	第 413 场周赛 Q3	位运算 数组 动态规划 状态压缩 矩阵

3276. 选择矩阵中单元格的最大得分

English Version

题目描述

给你一个由正整数构成的二维矩阵 grid。

你需要从矩阵中选择 一个或多个 单元格，选中的单元格应满足以下条件：

• 所选单元格中的任意两个单元格都不会处于矩阵的 同一行。
• 所选单元格的值 互不相同。

你的得分为所选单元格值的总和。

返回你能获得的 最大 得分。

 

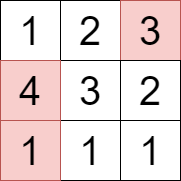
示例 1：

输入： grid = [[1,2,3],[4,3,2],[1,1,1]]

输出： 8

解释：

选择上图中用彩色标记的单元格，对应的值分别为 1、3 和 4 。

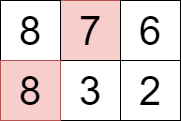
示例 2：

输入： grid = [[8,7,6],[8,3,2]]

输出： 15

解释：

选择上图中用彩色标记的单元格，对应的值分别为 7 和 8 。

 

提示：

• 1 <= grid.length, grid[i].length <= 10
• 1 <= grid[i][j] <= 100

解法

方法一：状态压缩动态规划

我们定义 $f[i][j]$ 表示在 $[1,..i]$ 的数中进行选择，且选择的数对应的行的状态为 $j$ 时的最大得分。初始时 $f[i][j] = 0$，答案为 $f[\textit{mx}][2^m - 1]$。其中 $\textit{mx}$ 表示矩阵中的最大值，而 $m$ 表示矩阵的行数。

我们首先对矩阵进行预处理，使用一个哈希表 $g$ 记录每个数对应的行的集合。然后我们可以使用状态压缩动态规划的方法求解答案。

对于状态 $f[i][j]$，我们可以不选择 $i$ 这个数，此时 $f[i][j] = f[i-1][j]$；也可以选择 $i$ 这个数，此时我们需要枚举 $i$ 对应的行的集合 $g[i]$ 中的每一个行 $k$，如果 $j$ 的第 $k$ 位为 $1$，则说明我们可以选择 $i$ 这个数，此时 $f[i][j] = \max(f[i][j], f[i-1][j \oplus 2^k] + i)$。

最后我们返回 $f[\textit{mx}][2^m - 1]$ 即可。

时间复杂度 $O(m \times 2^m \times \textit{mx})$，空间复杂度 $O(\textit{mx} \times 2^m)$。其中 $m$ 为矩阵的行数，而 $\textit{mx}$ 为矩阵中的最大值。

Python3

class Solution:
    def maxScore(self, grid: List[List[int]]) -> int:
        g = defaultdict(set)
        mx = 0
        for i, row in enumerate(grid):
            for x in row:
                g[x].add(i)
                mx = max(mx, x)
        m = len(grid)
        f = [[0] * (1 << m) for _ in range(mx + 1)]
        for i in range(1, mx + 1):
            for j in range(1 << m):
                f[i][j] = f[i - 1][j]
                for k in g[i]:
                    if j >> k & 1:
                        f[i][j] = max(f[i][j], f[i - 1][j ^ 1 << k] + i)
        return f[-1][-1]

Java

class Solution {
    public int maxScore(List<List<Integer>> grid) {
        int m = grid.size();
        int mx = 0;
        boolean[][] g = new boolean[101][m + 1];
        for (int i = 0; i < m; ++i) {
            for (int x : grid.get(i)) {
                g[x][i] = true;
                mx = Math.max(mx, x);
            }
        }
        int[][] f = new int[mx + 1][1 << m];
        for (int i = 1; i <= mx; ++i) {
            for (int j = 0; j < 1 << m; ++j) {
                f[i][j] = f[i - 1][j];
                for (int k = 0; k < m; ++k) {
                    if (g[i][k] && (j >> k & 1) == 1) {
                        f[i][j] = Math.max(f[i][j], f[i - 1][j ^ 1 << k] + i);
                    }
                }
            }
        }
        return f[mx][(1 << m) - 1];
    }
}

C++

class Solution {
public:
    int maxScore(vector<vector<int>>& grid) {
        int m = grid.size();
        int mx = 0;
        bool g[101][11]{};
        for (int i = 0; i < m; ++i) {
            for (int x : grid[i]) {
                g[x][i] = true;
                mx = max(mx, x);
            }
        }
        int f[mx + 1][1 << m];
        memset(f, 0, sizeof(f));
        for (int i = 1; i <= mx; ++i) {
            for (int j = 0; j < 1 << m; ++j) {
                f[i][j] = f[i - 1][j];
                for (int k = 0; k < m; ++k) {
                    if (g[i][k] && (j >> k & 1) == 1) {
                        f[i][j] = max(f[i][j], f[i - 1][j ^ 1 << k] + i);
                    }
                }
            }
        }
        return f[mx][(1 << m) - 1];
    }
};

Go

func maxScore(grid [][]int) int {
	m := len(grid)
	mx := 0
	g := [101][11]bool{}
	for i, row := range grid {
		for _, x := range row {
			g[x][i] = true
			mx = max(mx, x)
		}
	}
	f := make([][]int, mx+1)
	for i := range f {
		f[i] = make([]int, 1<<m)
	}
	for i := 1; i <= mx; i++ {
		for j := 0; j < 1<<m; j++ {
			f[i][j] = f[i-1][j]
			for k := 0; k < m; k++ {
				if g[i][k] && (j>>k&1) == 1 {
					f[i][j] = max(f[i][j], f[i-1][j^1<<k]+i)
				}
			}
		}
	}
	return f[mx][1<<m-1]
}

TypeScript

function maxScore(grid: number[][]): number {
    const m = grid.length;
    let mx = 0;
    const g: boolean[][] = Array.from({ length: 101 }, () => Array(m + 1).fill(false));
    for (let i = 0; i < m; ++i) {
        for (const x of grid[i]) {
            g[x][i] = true;
            mx = Math.max(mx, x);
        }
    }
    const f: number[][] = Array.from({ length: mx + 1 }, () => Array(1 << m).fill(0));
    for (let i = 1; i <= mx; ++i) {
        for (let j = 0; j < 1 << m; ++j) {
            f[i][j] = f[i - 1][j];
            for (let k = 0; k < m; ++k) {
                if (g[i][k] && ((j >> k) & 1) === 1) {
                    f[i][j] = Math.max(f[i][j], f[i - 1][j ^ (1 << k)] + i);
                }
            }
        }
    }
    return f[mx][(1 << m) - 1];
}