README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Hard	https://github.com/doocs/leetcode/edit/main/solution/2300-2399/2360.Longest%20Cycle%20in%20a%20Graph/README_EN.md	1897	Weekly Contest 304 Q4	Depth-First Search Graph Topological Sort

2360. Longest Cycle in a Graph

中文文档

Description

You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.

Return the length of the longest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node.

 

Example 1:

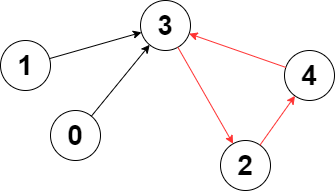
Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.

Example 2:

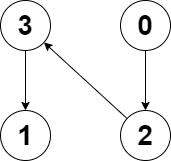
Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.

 

Constraints:

• n == edges.length
• 2 <= n <= 105
• -1 <= edges[i] < n
• edges[i] != i

Solutions

Solution 1: Traverse Starting Points

We can traverse each node in the range $[0,..,n-1]$. If a node has not been visited, we start from this node and search for adjacent nodes until we encounter a cycle or a node that has already been visited. If we encounter a cycle, we update the answer.

The time complexity is $O(n)$ and the space complexity is $O(n)$, where $n$ is the number of nodes.

Similar problems:

• 2127. Maximum Employees to Be Invited to a Meeting

Python3

class Solution:
    def longestCycle(self, edges: List[int]) -> int:
        n = len(edges)
        vis = [False] * n
        ans = -1
        for i in range(n):
            if vis[i]:
                continue
            j = i
            cycle = []
            while j != -1 and not vis[j]:
                vis[j] = True
                cycle.append(j)
                j = edges[j]
            if j == -1:
                continue
            m = len(cycle)
            k = next((k for k in range(m) if cycle[k] == j), inf)
            ans = max(ans, m - k)
        return ans

Java

class Solution {
    public int longestCycle(int[] edges) {
        int n = edges.length;
        boolean[] vis = new boolean[n];
        int ans = -1;
        for (int i = 0; i < n; ++i) {
            if (vis[i]) {
                continue;
            }
            int j = i;
            List<Integer> cycle = new ArrayList<>();
            for (; j != -1 && !vis[j]; j = edges[j]) {
                vis[j] = true;
                cycle.add(j);
            }
            if (j == -1) {
                continue;
            }
            for (int k = 0; k < cycle.size(); ++k) {
                if (cycle.get(k) == j) {
                    ans = Math.max(ans, cycle.size() - k);
                    break;
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int longestCycle(vector<int>& edges) {
        int n = edges.size();
        vector<bool> vis(n);
        int ans = -1;
        for (int i = 0; i < n; ++i) {
            if (vis[i]) {
                continue;
            }
            int j = i;
            vector<int> cycle;
            for (; j != -1 && !vis[j]; j = edges[j]) {
                vis[j] = true;
                cycle.push_back(j);
            }
            if (j == -1) {
                continue;
            }
            for (int k = 0; k < cycle.size(); ++k) {
                if (cycle[k] == j) {
                    ans = max(ans, (int) cycle.size() - k);
                    break;
                }
            }
        }
        return ans;
    }
};

Go

func longestCycle(edges []int) int {
	vis := make([]bool, len(edges))
	ans := -1
	for i := range edges {
		if vis[i] {
			continue
		}
		j := i
		cycle := []int{}
		for ; j != -1 && !vis[j]; j = edges[j] {
			vis[j] = true
			cycle = append(cycle, j)
		}
		if j == -1 {
			continue
		}
		for k := range cycle {
			if cycle[k] == j {
				ans = max(ans, len(cycle)-k)
				break
			}
		}
	}
	return ans
}

TypeScript

function longestCycle(edges: number[]): number {
    const n = edges.length;
    const vis = new Array(n).fill(false);
    let ans = -1;
    for (let i = 0; i < n; ++i) {
        if (vis[i]) {
            continue;
        }
        let j = i;
        const cycle: number[] = [];
        for (; j != -1 && !vis[j]; j = edges[j]) {
            vis[j] = true;
            cycle.push(j);
        }
        if (j == -1) {
            continue;
        }
        for (let k = 0; k < cycle.length; ++k) {
            if (cycle[k] == j) {
                ans = Math.max(ans, cycle.length - k);
                break;
            }
        }
    }
    return ans;
}