README.md

Logistic Regression

Logistic regression is the appropriate regression analysis to conduct when the dependent variable is dichotomous (binary). Like all regression analyses, the logistic regression is a predictive analysis. Logistic regression is used to describe data and to explain the relationship between one dependent binary variable and one or more nominal, ordinal, interval or ratio-level independent variables.

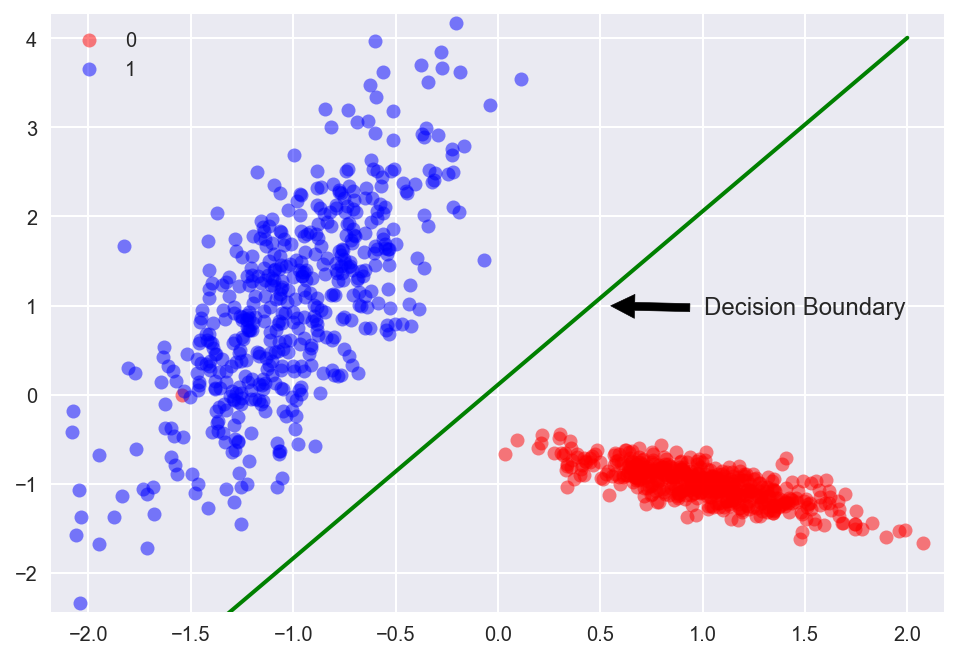
Logistic Regression is used when the dependent variable (target) is categorical.

For example:

• To predict whether an email is spam (1) or (0).
• Whether online transaction is fraudulent (1) or not (0).
• Whether the tumor is malignant (1) or not (0).

In other words the dependant variable (output) for logistic regression model may be described as:

Training Set

Training set is an input data where for every predefined set of features x we have a correct classification y.

m - number of training set examples.

For convenience of notation, define:

Hypothesis (the Model)

The equation that gets features and parameters as an input and predicts the value as an output (i.e. predict if the email is spam or not based on some email characteristics).

Where g() is a sigmoid function.

Now we my write down the hypothesis as follows:

Cost Function

Function that shows how accurate the predictions of the hypothesis are with current set of parameters.

Cost function may be simplified to the following one-liner:

Batch Gradient Descent

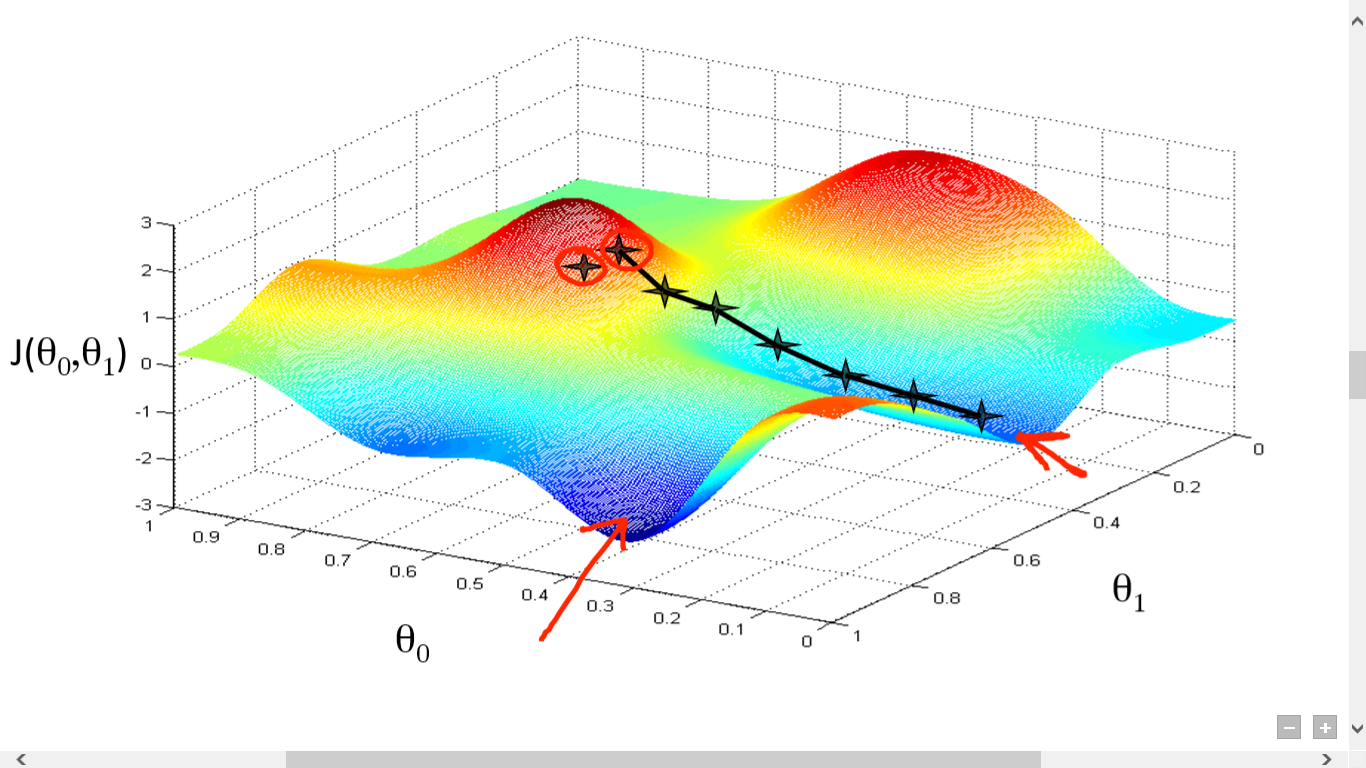
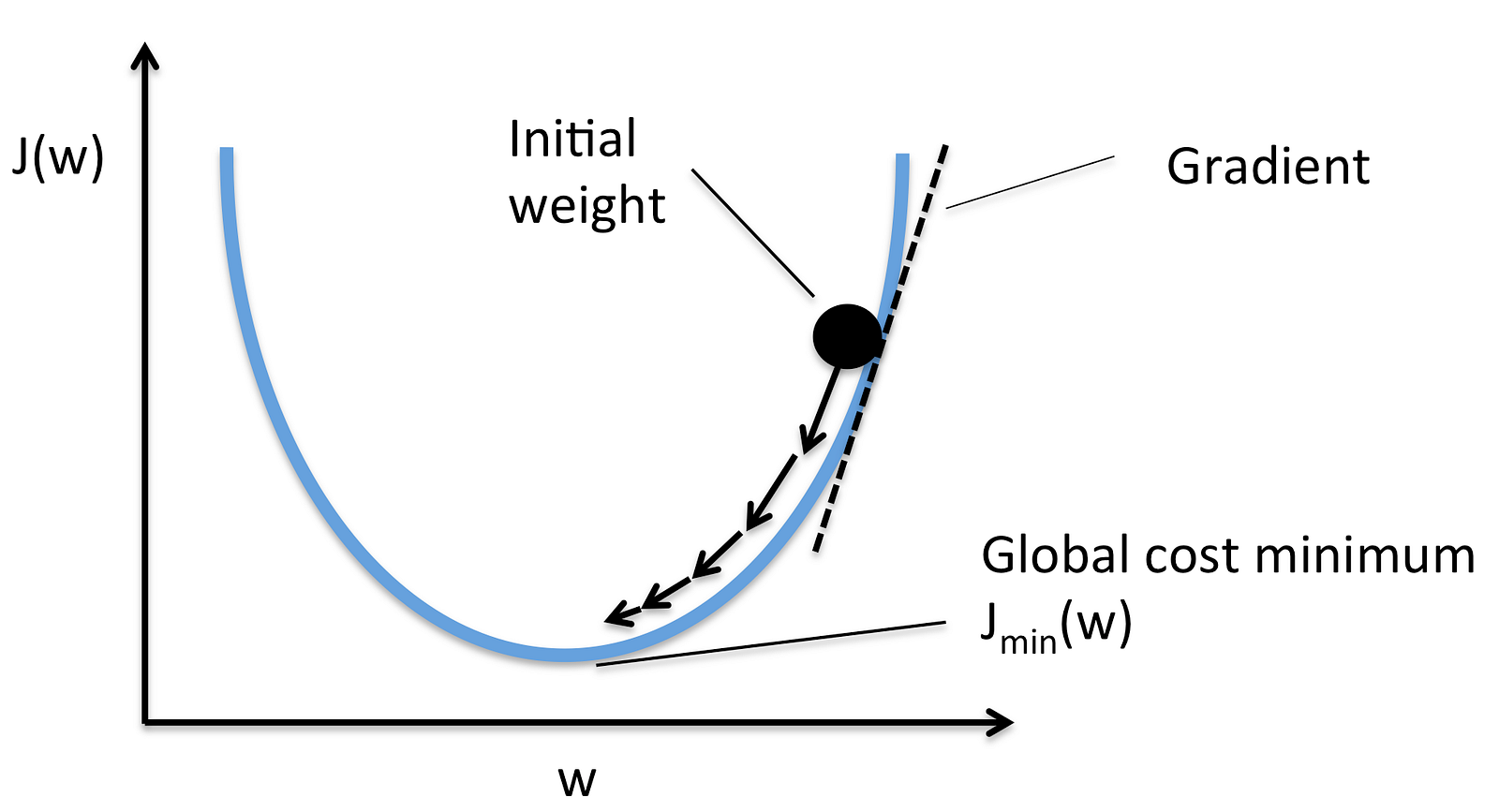
Gradient descent is an iterative optimization algorithm for finding the minimum of a cost function described above. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient (or approximate gradient) of the function at the current point.

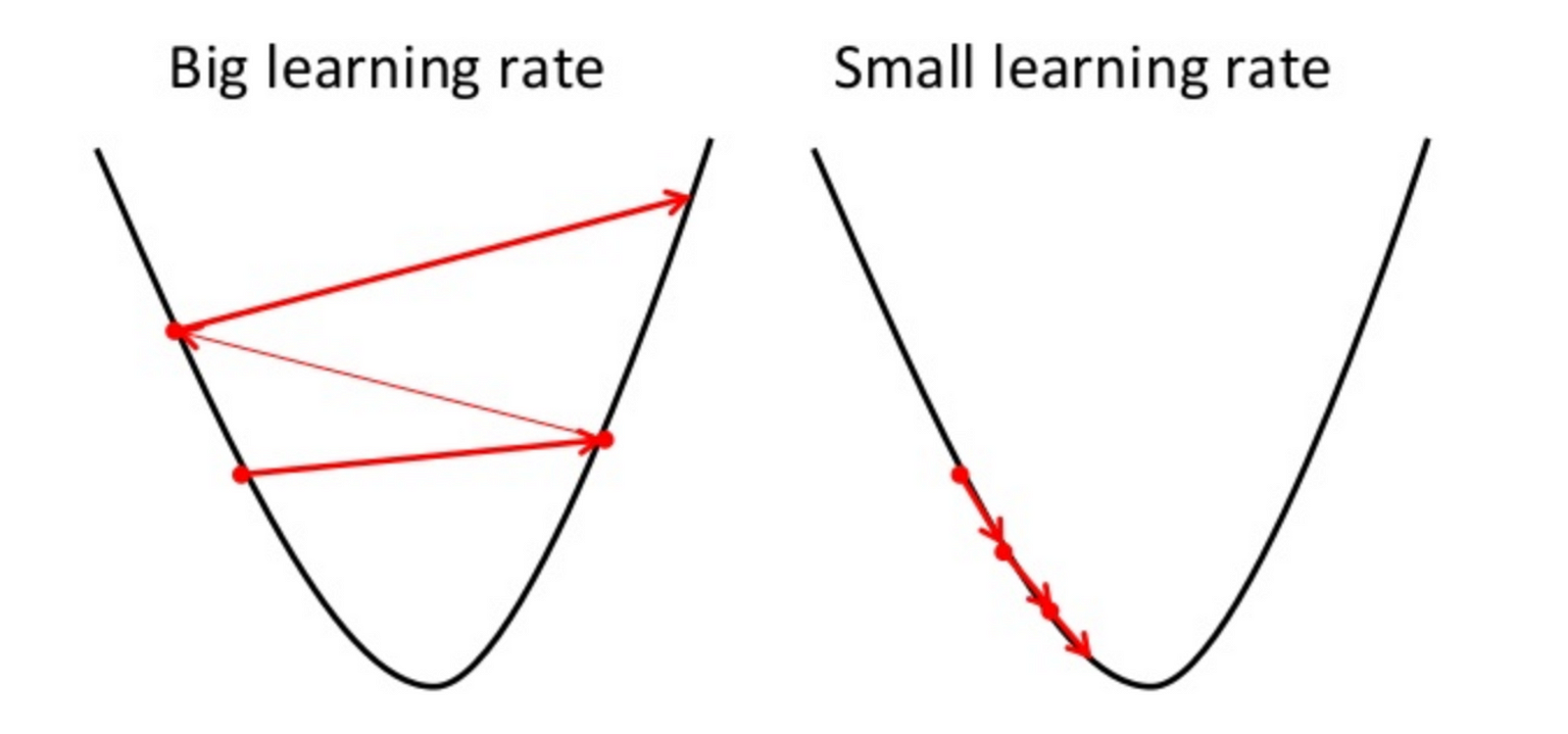
Picture below illustrates the steps we take going down of the hill to find local minimum.

The direction of the step is defined by derivative of the cost function in current point.

Once we decided what direction we need to go we need to decide what the size of the step we need to take.

We need to simultaneously update for j = 0, 1, ..., n

- the learning rate, the constant that defines the size of the gradient descent step

- j^th feature value of the i^th training example

- input (features) of i^th training example

yⁱ - output of i^th training example

m - number of training examples

n - number of features

When we use term "batch" for gradient descent it means that each step of gradient descent uses all the training examples (as you might see from the formula above).

Multi-class Classification (One-vs-All)

Very often we need to do not just binary (0/1) classification but rather multi-class ones, like:

• Weather: Sunny, Cloudy, Rain, Snow
• Email tagging: Work, Friends, Family

To handle these type of issues we may train a logistic regression classifier several times for each class i to predict the probability that y = i.

Regularization

Overfitting Problem

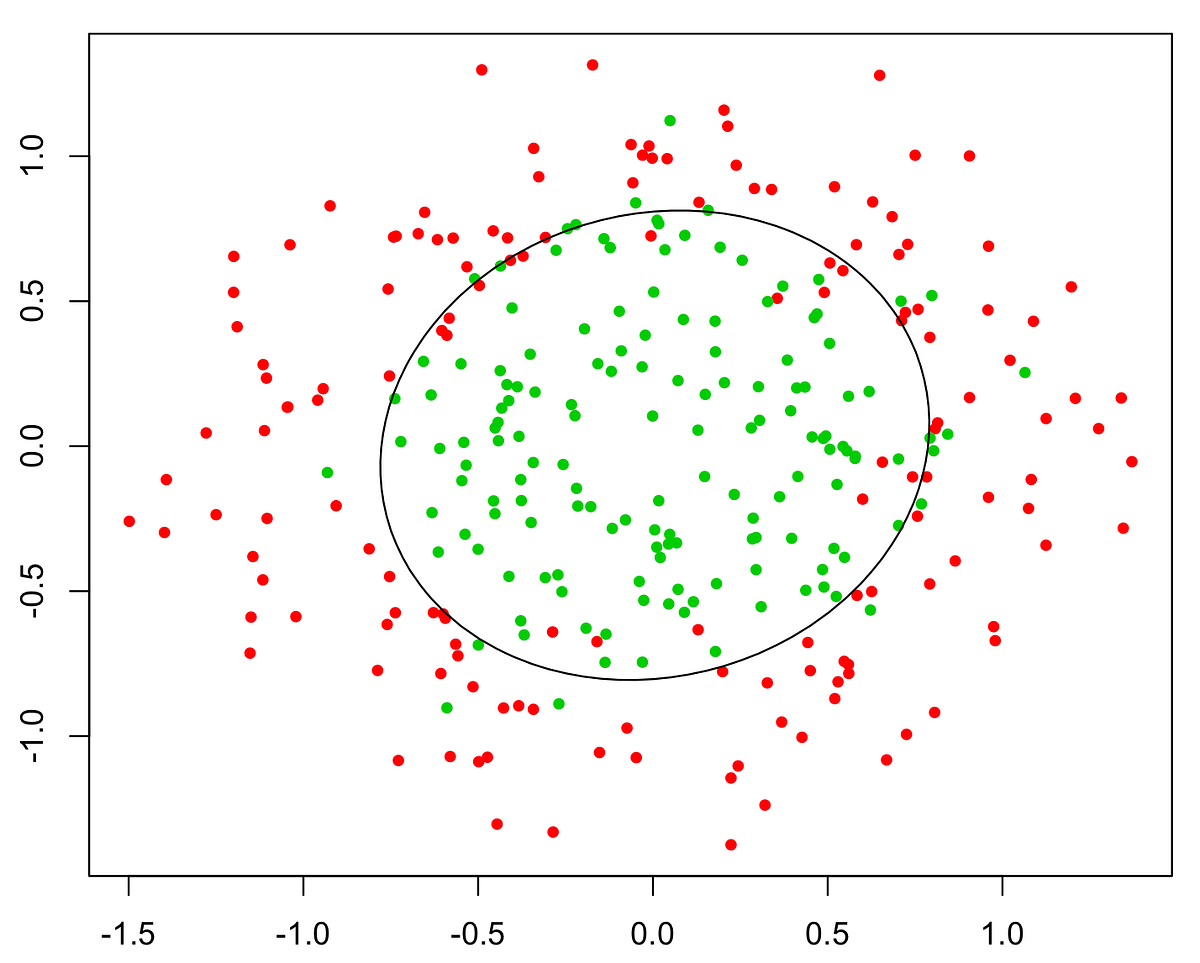
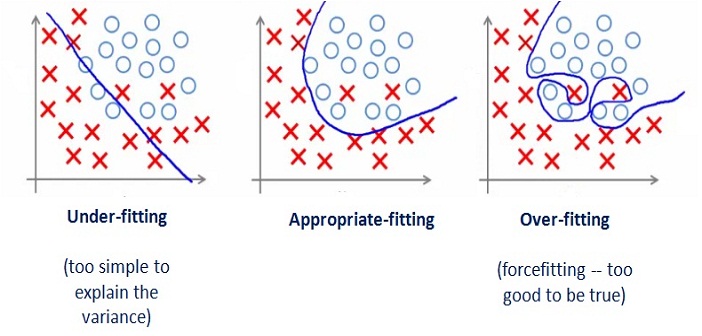
If we have too many features, the learned hypothesis may fit the training set very well:

But it may fail to generalize to new examples (let's say predict prices on new example of detecting if new messages are spam).

Solution to Overfitting

Here are couple of options that may be addressed:

• Reduce the number of features
  • Manually select which features to keep
  • Model selection algorithm
• Regularization
  • Keep all the features, but reduce magnitude/values of model parameters (thetas).
  • Works well when we have a lot of features, each of which contributes a bit to predicting y.

Regularization works by adding regularization parameter to the cost function:

- regularization parameter

Note that you should not regularize the parameter .

In this case the gradient descent formula will look like the following:

Files

• demo.m - logistic regression demo script that loads test data and plots decision predictions.
• logistic_regression_train.m - logistic regression algorithm.
• hypothesis.m - logistic regression hypothesis function.
• cost_function.m - logistic regression cost function.
• gradient_descent.m - function that performs gradient descent.
• gradient_step.m - function that performs just one gradient descent step.
• gradient_callback.m - function that aggregates gradient step and cost function values for fminunc.
• microchips_tests.csv - training data set of microchip parameters and their validity.
• digits.mat - training set of labeled hand-written digits.
• add_polynomial_features.m - function that generates new polynomial features for training set in order to make decision boundaries to have complex form.
• one_vs_all.m - trains 10 logistic regression model each of which recognizes specific number starting from 0 to 9.
• one_vs_all_predict.m - predicts what the digit is written based on one-vs-all logistic regression approach.
• fmincg.m - function that does gradient descent as ans alternative to fminunc().
• display_data.m - function that displays training set hand-written digits.
• sigmoid.m - sigmoid function.

Demo visualizations

References

• Machine Learning on Coursera
• Sigmoid Function on Wikipedia
• Gradient Descent on Wikipedia
• Gradient Descent by Suryansh S.
• Gradient Descent by Niklas Donges
• One vs All on Stackexchange
• Logistic Regression by Rohan Kapur
• Overfitting on GeeksForGeeks