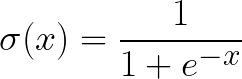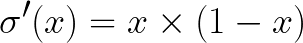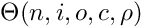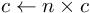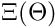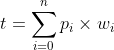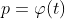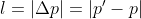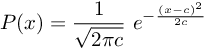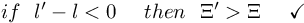These are the core principles of object-oriented approach to the current state of artificial neural networks that is inspired by synaptic plasticity between biological neurons:
- Unlike the current ANN implementations, neurons must be objects not tensors between matrices.
- Just the current ANN implementations, neurons should be GPU accelerated (ideally) to provide the necessary parallelism.
- While the current ANN implementations can only create special cases, a Plexus Network must be architecture-free (i.e. adaptive) to create a generalized solution of all machine learning problems.
- Instead of dealing with decision of choosing an ANN layer combination(such as Convolution, Pooling or Recurrent layers), the network must have a layerless design.
- There must be fundamentally two types of neurons: sensory neuron, interneuron.
- Input of the network must be made of sensory neurons. Any interneuron can be picked as a motor neuron (an element of the output). There are literally no difference between an interneuron and a motor neuron except the intervene of the network for igniting the wick of learning process through the motor neurons. Any non-motor interneuron can be assumed as a cognitive neuron which collectively forms the cognition of network.
- There can be arbitrary amount of I/O groups in a single network.
- Instead of batch size, iteration, and epoch concepts, training examples must be fed on time basis with a manner like; learn first sample for X seconds, OK done? then learn second sample for Y seconds. By this approach, you can assign importance factors to your samples with maximum flexibility.
- Network must be retrainable.
- Network must be modular. In other words: You must be able to train a small network and then plug that network into a bigger network (we are talking about some kind of self-fusing here).
- Neurons must exhibit the characteristics of cellular automata just like Conway's Game of Life.
- Number of neurons in the network can be increased or decreased (scalability).
- There must be no need for a network-wide oscillation. Yet the execution of neurons should follow a path very similar to flow of electric current nevertheless.
- Network should use randomness and/or uncertainty principle flawlessly. Consciousness is an emergent property from cellular level to macro scale, the network. But it's also an emergent property for the neuron from quantum level uncertainty to cellular mechanisms. In such a way that randomness is the cause of the illusion of consciousness.
- Most importantly, the network must and can not iterate through the whole dataset. Besides that, it's also generally impossible to iterate the whole dataset on real life situations if the system is continuous like in robotics. Because of that; the network must be designed to handle such a continuous data stream that literally endless and must be designed to handle that data stream chunk by chunk. Therefore, when you are feeding the network, use a diverse feed but not a grouped feed (like 123123123123123123 but not like 111111222222333333).
The activation function that used by Plexus is Sigmoid:
and the derivative of the Sigmoid function:
Implementation of this algorithm in Python programming language is publicly accessible through this link: https://github.com/mertyildiran/Plexus/blob/master/plexus/plexus.py
You can directly skip to Application part if you are not willing to understand the mathematical and algorithmic background.
Plexus Network has only two classes; Network and Neuron. In a Plexus Network, there are many instances of Neuron class but there is only one instance of Network class.
When you crate a new Plexus Network you give these five parameters to the Network class: size of the network, input dimension, output dimension, connectivity rate, precision. The network accordingly builds itself.
- size is literally equal to total number of neurons in the network. All neurons are referenced in an instance variable called
Network.neurons - input dimension specifies the number of sensory neurons. Sensory neurons are randomly selected from neurons.
- output dimension specifies the number of motor neurons. Motor neurons are randomly selected from non-sensory neurons.
- number of neurons multiplied by connectivity rate gives the average number of subscriptions made by a single neuron.
- precision simply defines the precision of the all calculations will be made by neurons (how many digits after the decimal point).
After the network has been successfully created. It will ignite itself automatically. Ignition in simple terms, no matter if you have plugged in some data or not, it will fire the neurons with using some mechanism very similar to flow of electric current (will be explained later on this paper).
A single neuron in a Plexus Network, takes the network as the only parameter and stores these seven very important information (in it's instance variables): subscriptions, publications, potential, desired_potential, loss and type
There are eventually there types of neurons:
Neuron.type = 1means it's a sensory neuron.Neuron.type = 2means it's a motor neuron.Neuron.type = 0means it's neither a sensory nor a motor neuron. It means it's an cognitive interneuron (or just cognitive neuron).
Functionality of a neuron is relative to its type.
subscriptions is neuron's indirect data feed. Each non-sensory neuron subscribes to some other neurons of any type. For sensory neurons, subscriptions are completely meaningless and empty by default because it gets its data feed from outside world by assignments of the network. Subscriptions are literally the Plexus Network equivalent of Dendrites in biological neurons. subscriptions is a dictionary that holds Neuron(reference) as key and Weight as value.
publications holds literally the mirror data of subscriptions in the target neurons. In other words; any subscription creates also a publication reference in the target neuron. Similarly, publications is the Plexus Network equivalent of Axons in biological neurons.
potential p is the overall total potential value of all subscriptions multiplied by the corresponding weights. Only in sensory neurons, it is directly assigned by the network. Value of potential may only be updated by the neuron's itself and its being calculated by this simple formula each time when the neuron is fired:
desired_potential p' is the ideal value of the neuron's potential that is desired to eventually reach. For sensory neurons, it is meaningless. For motor neurons, it is assigned by the network. If it's None then the neuron does not learn anything and just calculates potential when it's fired.
loss l is calculated not just at the output but in every neuron except sensory ones and it is equal to absolute difference (distance) between desired potential and current potential.
All numerical values inside a neuron are floating point numbers and all the calculations obey to the precision that given at start.
Input Layer in classical neural networks renamed as Sensory Neurons in Plexus networks, and Target/Output Layer renamed as Motor Neurons. This naming convention is necessary cause the built of the relevance of artificial neural networks with biological neural networks and Neuroscience.
The difference of sensory neurons from the cognitive neurons (that neither sensory nor motor ones) is, they do not actually fire. They just stand still for the data load. They do not have any subscriptions to the other neurons (literally no subscriptions). But they can be subscribed by the other neurons, including motor ones. They do not learn, they do not consume any CPU resources. They just stored in the memory. You can assign an image, a frame of a video, or a chunk of an audio to a group of sensory neurons.
The difference of motor neurons form the other neurons is, they are only responsible to the network. They act as the fuse of the learning and calculation of the loss. The network dictates a desired potential on each motor neuron. The motor neuron calculates its potential, compares it with desired potential, calculates the loss then tries to update its weights randomly many times and if it fails, it blames its subscriptions. So just like the network, motor neurons are also able to dictate a desired potential on the other non-motor neurons. This is why any neuron holds an additional potential variable called desired_potential.
On the second phase of the network initiation, any non-sensory neurons are forced to subscribe to some non-motor neurons which are selected by random sampling. Length of this sample is also selected by random sampling (rounds to nearest integer) is done from a normal distribution. Such a normal distribution that, the average number of subscriptions is the mean, and square root of the mean is the standard deviation. (e.g. if neurons on average has 100 subscriptions then the mean is 100 and the standard deviation is 10)
Even so the Python implementation of Plexus Network is easy to understand, it will be helpful for readers to explain the algorithm in pseudocode;
procedure initiate the network is
connectivity ← size * connectivity_rate;
connectivity_sqrt ← sqrt(connectivity);
connectivity_sqrt_sqrt ← sqrt(connectivity_sqrt);
for item in size, do
create neuron;
end
pick sensory neurons randomly;
pick motor neurons randomly;
determine non-sensory neurons;
determine non-motor neurons;
initiate subscriptions;
initiate instance variables;
ignite the network;Initiation is nothing more than a make the assignments for once phase until the ignition. The final step (ignition) never stops but can be paused (if user wants).
procedure initiate subscriptions is
for neuron in neurons, do
if neuron is not a sensory neuron, then
call neuron.partially_subscribe();
end
end
return True;procedure partially subscribe is
sample ← randomly sample approximately "connectivity" units of a neuron from within all non-motor neurons;
for neuron in sample, do
if neuron is not self, then
establish a subscription; // weight is randomly assigned
establish a publication;
end
end
return True;The time complexity of the procedure initiate subscriptions is O(n2), so this may take a while if the size of the network and connectivity is big.
procedure ignite subscriptions is
create an empty ban_list;
while network is not frozen, do
if next_queue is empty, then
get the output of network and print it;
increase the wave_counter;
if first_queue is empty, then
for neuron in sensory neurons, do
for target_neuron in neuron.publications, do
append target_neuron to first_queue;
end
end
copy first_queue to next_queue;
end
end
copy next_queue to current_queue;
empty next_queue;
for neuron in ban_list, do
if neuron.ban_counter > connectivity_sqrt_sqrt, then
remove the neuron from current_queue;
end
end
while current_queue is not empty, do
neuron ← select a random neuron from current_queue;
remove the neuron from current_queue;
if neuron.ban_counter <= connectivity_sqrt_sqrt, then
call neuron.fire();
append the neuron to ban_list;
increase neuron.ban_counter;
for target_neuron in neuron.publications, do
append target_neuron to next_queue;
end
end
end
endProcedure ignite regulates the firing order of neurons and creates an effect very similar to flow of electric current, network wide. It continuously runs until the network frozen, nothing else can stop it. It fires the neurons step by step through adding them to a queue.
It generates its first queue from the publications of sensory neurons. Time complexity of if next_queue is empty, then block is O(n2) but it can be ignored (unless there are too many sensory neurons) because it runs once per wave.
It eliminates banned neurons with for neuron in ban_list, do block. Function of ban_counter is giving neurons connectivity_sqrt_sqrt amount of chance after they added to ban_list. Then it fires the neurons inside current_queue, one by one, choosing them randomly.
After a neuron fired, it adds the fired neuron to ban_list and lastly copies the publications of that neuron to next_queue so execution(firing process) can follow the path through the connections.
Each execution from first sensory neuron to last motor neuron symbolizes one wave. Every time a wave finished, procedure falls into if next_queue is empty, then block so wave starts over from the sensory neurons.
ban_counter and connectivity_sqrt_sqrt comparison creates execution loops inside cognitive neurons and these loops act like memory units which is a pretty important concept. Because loops create the relation between currently fed data and previously learned data. Without these loops the network fails on both classification and regression problems.
Because neuron.fire() has a time complexity of O(n2), each turn inside while network is not frozen, do block, has a time complexity of O(n4). But don't worry because it will approximate to O(n3) because of the probabilistic nature of fire function and the network will fire more than a million of neurons per minute. By the way, while network is not frozen, do block is ignored because it's an endless loop under normal conditions.
procedure fire is
if self is not a sensory neuron, then
potential ← calculate potential;
increase fire counter;
if desired_potential is not None, then
loss ← calculate loss;
if loss = 0, then
desired_potential ← None;
return True;
end
if blame_lock is not empty, then
if (wave_counter - blame_lock) < connectivity, then
return True;
else
blame_lock ← None;
end
try connectivity times:
generate new weights randomly;
calculate new potential and new loss according to these weights;
if loss_new < loss_current, then return True;
end
try sqrt(connectivity) times:
generate hypothetical potentials for neurons in subscriptions randomly;
calculate new potential and new loss according to these hypothetical potentials;
if loss_new < loss_current, then
apply these hypothetical potentials as "desired_potential"s;
return True;
end
end
if (still) not improved, then
either create some new subscriptions;
or break some of the subscriptions;
return True;
end
end
endProcedure fire handles all feedforwarding, backpropagation and learning process by itself. fire function is an instance method of Neuron class. This procedure is by far the most important one in the Plexus Network. It's basically the core function and CPU spends most of its time to execute fire functions again and again.
If desired_potential is not assigned to a value, then it just calculates the potential and finishes.
If desired_potential is assigned to a value, then first it calculates the loss. If loss is equal to zero, then the current state of the neuron is perfectly well and there is nothing to learn.
If blame_lock is not empty, then it will pass this function connectivity times with this control statement: if blame_lock is not empty, then.
It tries to improve the current state of the neuron by updating its weights randomly, connectivity times. If it's improved, then break.
It tries to improve the current state of the neuron by dictating randomly generated hypothetical potentials over the subscriptions, square root of connectivity times. If it's improved, then break.
If it still is not improved, then it either creates some new subscriptions or breaks some of the subscriptions it currently has and hopes it will lead the neuron to new improvements in the future.
On the first wave, the fire function is only meaningful for motor neurons but after the first wave desired_potential dictation will spread throughout the cognitive neurons.
procedure load (input, output) is
if output is None, then
for neuron in motor neurons, do
neuron.desired_potential ← None;
end
end
if (number of sensory neurons is not equal to input length), then
raise an error but do not interrupt the network;
else
for neuron in sensory neurons, do
neuron.potential ← load from the input;
end
end
if (number of motor neurons is not equal to output length), then
raise an error but do not interrupt the network;
else
for neuron in motor neurons, do
neuron.desired_potential ← load from the output;
end
endProcedure load is the only method that you can feed your data to the network. You should call that function and load your data in real time. Also you should do it periodically and continuously, like every 3 seconds. If you leave second parameter empty then this procedure will automatically assume that you are testing the network, so it will replace desired_potential values of motor neurons with None. Otherwise, it means you are training the network so it will load the input data to sensory neurons and it will load the output data to desired_potential values of motor neurons.
pip install plexusIf you want to install Plexus on development mode:
git clone https://github.com/mertyildiran/Plexus.git
cd Plexus/
pip install -e .or alternatively:
make devand test the installation with:
make cpp(you can alternatively run this example with python3 examples/classification_binary.py command using a pre-written script version of below commands)
Suppose you need to train the network to figure out that the elements of given arrays are bigger than 0.5 or not (like [0.9, 0.6, 1.0, 0.8] or [0.1, 0.3, 0.0, 0.4]) and suppose it's a 4-element array. So let's create a network according to your needs:
import cplexus as plexus
SIZE = 14
INPUT_SIZE = 4
OUTPUT_SIZE = 2
CONNECTIVITY = 1
PRECISION = 2
RANDOMLY_FIRE = False
DYNAMIC_OUTPUT = True
VISUALIZATION = False
net = plexus.Network(
SIZE,
INPUT_SIZE,
OUTPUT_SIZE,
CONNECTIVITY,
PRECISION,
RANDOMLY_FIRE,
DYNAMIC_OUTPUT,
VISUALIZATION
)If you want to visualize the network using PyQtGraph enable VISUALIZATION = False. Because our network is automatically initiated and ignited, now all we have to do is training the network. So let's train our network with 80 samples:
PRECISION = 2
TRAINING_SAMPLE_SIZE = 20
for i in range(1, TRAINING_SAMPLE_SIZE):
if (i % 2) == 0:
output = [1.0, 0.0]
generated_list = generate_list_bigger()
notify_the_load(generated_list, output, TRAINING_DURATION)
net.load(generated_list, output)
else:
output = [0.0, 1.0]
generated_list = generate_list_smaller()
notify_the_load(generated_list, output, TRAINING_DURATION)
net.load(generated_list, output)
time.sleep(TRAINING_DURATION)You should load your data one by one from each kind, respectively. Because it will prevent over fitting to one specific kind. You must wait a short time like TRAINING_DURATION = 0.01 seconds (which is a reasonable duration in such a case), after each load.
output[0] will converge to detect bigger than 0.5 inputs.
output[1] will converge to detect smaller than 0.5 inputs.
Before the testing you should define a criteria called DOMINANCE_THRESHOLD so you can catch the decision making. Now let's test the network:
error = 0
error_divisor = 0
for i in repeat(None, TESTING_SAMPLE_SIZE):
binary_random = random.randint(0, 1)
if binary_random == 0:
generated_list = generate_list_bigger()
expected = [1.0, 0.0]
else:
generated_list = generate_list_smaller()
expected = [0.0, 1.0]
net.load(generated_list)
time.sleep(TRAINING_DURATION)
output = net.output
error += abs(expected[0] - output[0])
error += abs(expected[1] - output[1])
error_divisor += 2With the while loop given above, you will be able to check the output by giving enough time to propagate your input throught the network. By giving net.load() only one parameter here, you automatically disable the training.
Now freeze your network and calculate the overall error:
net.freeze()
error = error / error_divisorwhich outputs:
Overall error: 0.010249996604397894
This example is quite simple to the previous example but this time we are teaching the network to understand if the given number is prime or not. Which is a relatively complex problem.
Run python3 examples/classification_prime.py 1 -l cpp to see the result. You will observe that the network is able to learn the solution for such a complex problem in the matter of seconds.
In this example, instead of classification, we will train the network to detect a pattern in given sequence. The magic here is; without even changing anything related to network, just by changing logic we feed the data into the network, the network automatically turns into a Recurrent Neural Network.
Run python3 examples/sequence_basic.py to see the output. This is the output you should see:
___ PLEXUS NETWORK BASIC SEQUENCE RECOGNITION EXAMPLE ___
Create a Plexus network with 14 neurons, 4 of them sensory, 1 of them motor, 1 connectivity rate, 2 digit precision
Precision of the network will be 0.01
Each individual non-sensory neuron will subscribe to 14 different neurons
14 neurons created
4 neuron picked as sensory neuron
1 neuron picked as motor neuron
Network has been ignited
*** LEARNING ***
Generate The Dataset (20 Items Long) To Recognize a Sequence & Learn for 0.1 Seconds Each
Load Input: [1.0, 0.0, 0.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 1.0, 0.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 0.0, 1.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 0.0, 0.0, 1.0] Output: [0.0] and wait 0.1 seconds
Load Input: [1.0, 0.0, 0.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 1.0, 0.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 0.0, 1.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 0.0, 0.0, 1.0] Output: [1.0] and wait 0.1 seconds
Load Input: [1.0, 0.0, 0.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 1.0, 0.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 0.0, 1.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 0.0, 0.0, 1.0] Output: [0.0] and wait 0.1 seconds
Load Input: [1.0, 0.0, 0.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 1.0, 0.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 0.0, 1.0, 0.0] Output: [0.0] and wait 0.1 seconds
Load Input: [0.0, 0.0, 0.0, 1.0] Output: [1.0] and wait 0.1 seconds
...
by looking at this output, you should be able to see the pattern. Now on testing stage you can see how successful the network is on detecting the pattern:
*** TESTING ***
Test the network with random data (20 times)
Load Input: ([1.0, 0.0, 0.0, 0.0], [0.0]) RESULT: 0.019999999552965164
Load Input: ([0.0, 1.0, 0.0, 0.0], [0.0]) RESULT: 0.0
Load Input: ([0.0, 0.0, 1.0, 0.0], [0.0]) RESULT: 0.019999999552965164
Load Input: ([0.0, 0.0, 0.0, 1.0], [0.0]) RESULT: 0.019999999552965164
Load Input: ([1.0, 0.0, 0.0, 0.0], [0.0]) RESULT: 0.0
Load Input: ([0.0, 1.0, 0.0, 0.0], [0.0]) RESULT: 0.0
Load Input: ([0.0, 0.0, 1.0, 0.0], [0.0]) RESULT: 0.05999999865889549
Load Input: ([0.0, 0.0, 0.0, 1.0], [1.0]) RESULT: 0.6600000262260437
Load Input: ([1.0, 0.0, 0.0, 0.0], [0.0]) RESULT: 0.019999999552965164
Load Input: ([0.0, 1.0, 0.0, 0.0], [0.0]) RESULT: 0.0
Load Input: ([0.0, 0.0, 1.0, 0.0], [0.0]) RESULT: 0.05999999865889549
Load Input: ([0.0, 0.0, 0.0, 1.0], [0.0]) RESULT: 0.6600000262260437
Load Input: ([1.0, 0.0, 0.0, 0.0], [0.0]) RESULT: 0.019999999552965164
Load Input: ([0.0, 1.0, 0.0, 0.0], [0.0]) RESULT: 0.0
Load Input: ([0.0, 0.0, 1.0, 0.0], [0.0]) RESULT: 0.0
Load Input: ([0.0, 0.0, 0.0, 1.0], [1.0]) RESULT: 0.9800000190734863
...
and the overall error:
Network is now frozen
1786760 waves are executed throughout the network
In total: 66110093 times a random non-sensory neuron is fired
Overall error: 0.040124996623490006
(you can alternatively run this example with python3 examples/catdog.py command using a pre-written script version of below commands)
Suppose you need to train the network to figure out that the given image (32x32 RGB) is an image of a cat or a dog and map them to blue and red respectively. So let's create a network according to your needs:
SIZE = 32 * 32 * 3 + 3 + 256
INPUT_SIZE = 32 * 32 * 3
OUTPUT_SIZE = 3
CONNECTIVITY = 0.005
PRECISION = 3
TRAINING_DURATION = 3
RANDOMLY_FIRE = False
DYNAMIC_OUTPUT = False
VISUALIZATION = False
net = plexus.Network(
SIZE,
INPUT_SIZE,
OUTPUT_SIZE,
CONNECTIVITY,
PRECISION,
RANDOMLY_FIRE,
DYNAMIC_OUTPUT,
VISUALIZATION
)We will plug in 32x32 RGB to the network so we need 3072 sensory neurons. 3 motor neurons for see how RGB our result is and 256 cognitive neurons to train. We need 3 digits precision because we need to store 255 different values between 0.0 and 1.0 range.
Explaining the answer of How to load CIFAR-10 dataset and use it is out of the scope of this paper but you can easily understand it by reading the code: examples/catdog.py Once you get the numpy array of CIFAR-10 (or any other image data) just normalize it and load:
TRAINING_SAMPLE_SIZE = 20
for i in range(1, TRAINING_SAMPLE_SIZE):
if (i % 2) == 0:
cat = random.sample(cats, 1)[0]
cat_normalized = np.true_divide(cat, 255).flatten()
blue_normalized = np.true_divide(blue, 255).flatten()
cv2.imshow("Input", cat)
net.load(cat_normalized, blue_normalized)
else:
dog = random.sample(dogs, 1)[0]
dog_normalized = np.true_divide(dog, 255).flatten()
red_normalized = np.true_divide(red, 255).flatten()
cv2.imshow("Input", dog)
net.load(dog_normalized, red_normalized)
show_output(net)You will get an Overall error as the result very similar to examples above although this time the input length was 768 times bigger. This is because Plexus Network amalgamates the problems from all levels of difficulty on a single medium. It makes easy problems relatively hard, and hard problems relatively easy.
When you run this example, you will get a slightly better result when compared to flipping a coin. You will most likely get an Overall error between 0.35 - 0.45 which is the proof that the network is able to learn something.
By the way, don't forget that; Plexus Network does not iterate over the dataset and furthermore it runs in real-time. Also you have trained the network just for 4-5 minutes. Now let's see what happens if we train our network for a long period of time:
Implementation of GPU acceleration and saving the trained network to disk are in work-in-progress (WIP) state. Therefore some parts of the implementation are subject to change.