HashMap是基于哈希表实现的,用于存储key-value的键值对,并允许使用null值和null键。由于是基于Hash表实现的,因此HashMap具有较高的查询效率,理想情况下HashMap的查找时间复杂度可达到O(1)。
(1)HashMap的存储结构
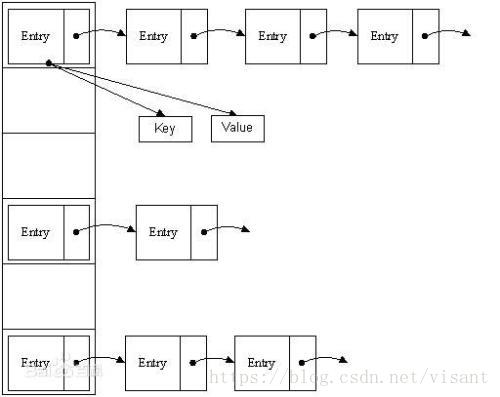
HashMap实际上是一个“链表散列”的数据结构,即数组和链表的结合体(链地址法处理冲突)。HashMap内部封装了一个包含key和value的Entry类,用于存储键值对。在put操作中会根据key的hashcode计算在哈希表中的存储位置,并将Entry存入该位置。由于存在Hash冲突的情况,HashMap采用了链地址法来处理Hash冲突。即使用链表的形式将相同哈希值的元素连起来。如下图所示:
(2) HashMap的扩容与ReHash 由于HashMap存的长度是确定的,可以初始化时候指定长度或者默认长度16。随着HashMap中插入的元素越来越多,发生哈希冲突的概率会越来越大,相应的查找的效率就会越来越低。这意味着影响哈希表性能的因素除了哈希函数与处理冲突的方法之外,还与哈希表的装填因子大小有关。
我们将哈希表中元素数与哈希表长度的比值称为装填因子。装填因子 α=
$\frac{哈希表中元素数}{哈希表长度}$
在HashMap中,装填因子的阈值为0.75,当装填因子大于0.75时则会出发HashMap的扩容机制。这里我们应该知道,扩容并不是在原数组基础上扩大容量,而是需要申请一个长度为原来2倍的新数组。因此,扩容之后就需要将原来的数据从旧数组中重新散列存放到扩容后的新数组。这个过程我们称之为Rehash。
Rehash的操作将会重新散列扩容前已经存储的数据,这一操作涉及大量的元素移动,是一个非常消耗性能的操作。因此,在开发中我们应该尽量避免Rehash的出现。比如,可以预估元素的个数,事先指定哈希表的长度,这样可以有效减少Rehash。
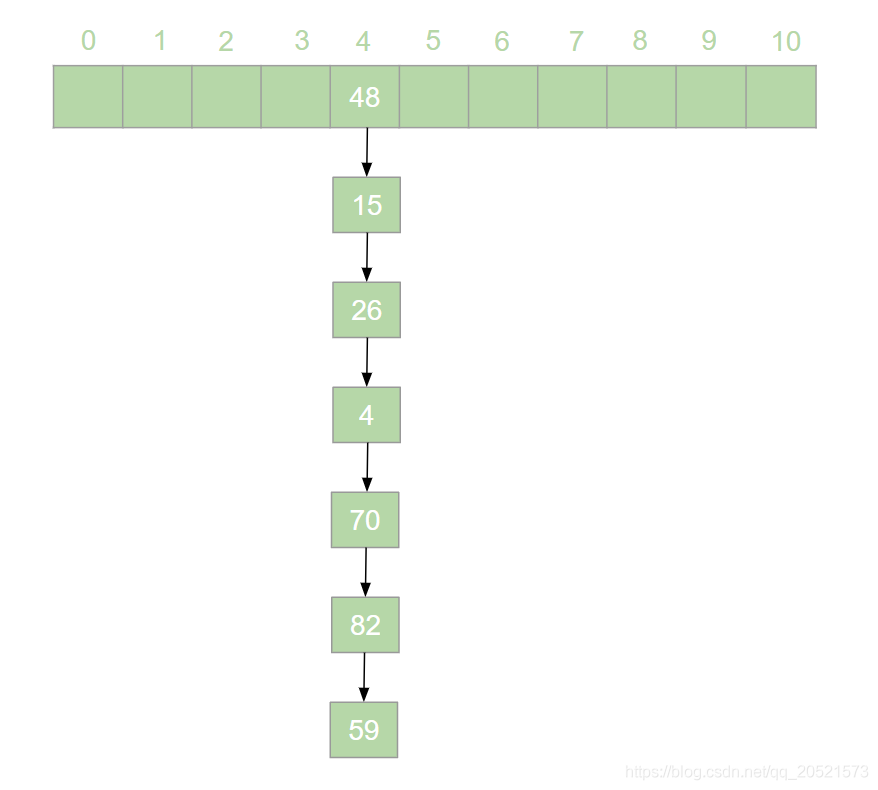
(3)JDK1.8中对HashMap的优化 JDK1.7 中,HashMap 采用位桶 + 链表的实现,即使用链表来处理冲突,同一 hash 值的链表都存储在一个数组中。但是当位于一个桶中的元素较多,即 hash 值相等的元素较多时,通过 key 值依次查找的效率较低。如下图所示的元素查找效率直接降低为了链表的时间复杂度o(n)
-
为了保证扩容后的数组索引与扩容前的数组索引一致
-
Rehash时的取余操作hash % length == hash & (length - 1)这个关系只有在length等于二的幂次方时成立
HashMap的初始容量是2的4次幂,扩容时候也是2的倍数。这样可以使添加的元素均匀的分布在HashMap中的数组上,减少Hash冲突。避免形成链表结构,进而提升查询效率。
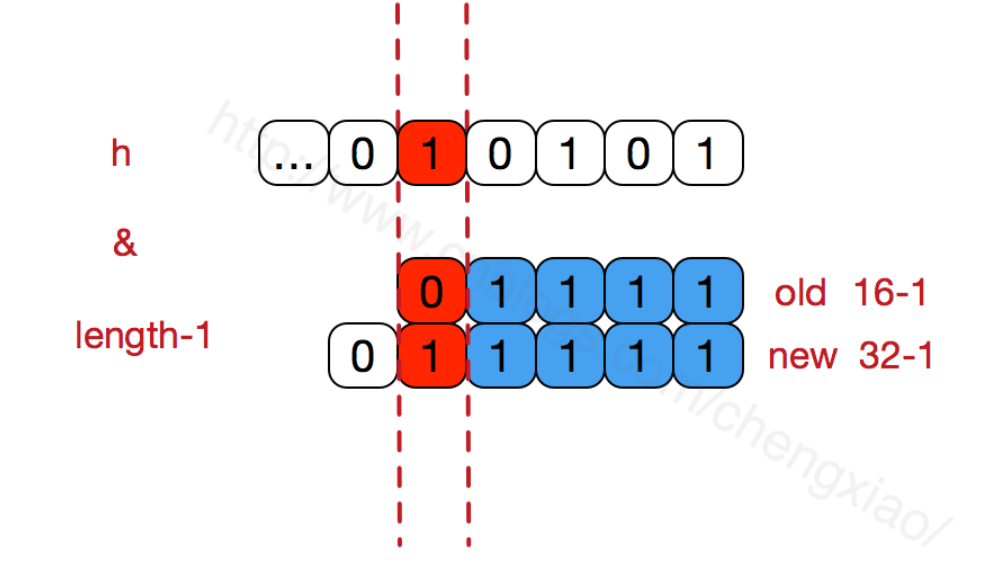
16的二进制表示为10000,length-1的二进制位表示为01111,扩容之后变为32,二进制表示为100000,减1之后的二进制位为011111。
扩容前后只有一位的差距,即相当于(32-1)>>1==(16-1)。如下图所示:
这样在通过has&(length-1)时,只要hash对应的最左边的哪一个差异位为0,就能保证到扩容后的数组和老数组的索引一致。
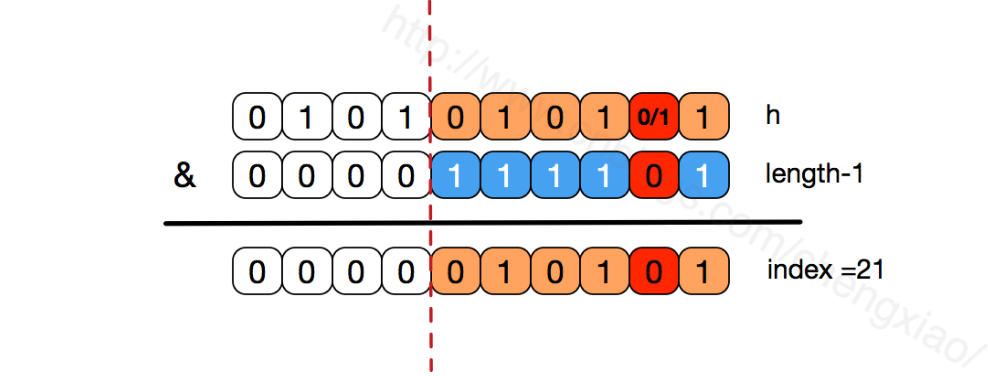
当数组长度保持2的次幂,length-1的低位都为1,这样会使得数组索引index更加均匀。如下图:
上面的&运算,高位是不会对结果产生影响的(hash函数采用各种位运算也是为了使得低位更加散列)。只关注低位的bit,如果低位全部为1,那么对于h低位部分来说任何一位的变化都会对结果产生影响。也就是说,只要得到index=21这个存储位置,h的低位只有这一种组合。这也是数组长度设计为2次幂的原因
如果不是2的次幂,也就是低位不是全为1此时,要使得index=21,h的低位部分不再具有唯一性了,哈希冲突的几率会变的更大,同时,index对应的这个bit位无论如何不会等于1了,而对应的那些数组位置也就被白白浪费了。