Skip to content

Latest commit

 

History

History
369 lines (327 loc) · 9.79 KB

README.md

File metadata and controls

369 lines (327 loc) · 9.79 KB

2415. 反转二叉树的奇数层

English Version

题目描述

给你一棵 完美 二叉树的根节点 root ，请你反转这棵树中每个 奇数 层的节点值。

  • 例如，假设第 3 层的节点值是 [2,1,3,4,7,11,29,18] ，那么反转后它应该变成 [18,29,11,7,4,3,1,2] 。

反转后，返回树的根节点。

完美 二叉树需满足：二叉树的所有父节点都有两个子节点，且所有叶子节点都在同一层。

节点的 层数 等于该节点到根节点之间的边数。

 

示例 1：

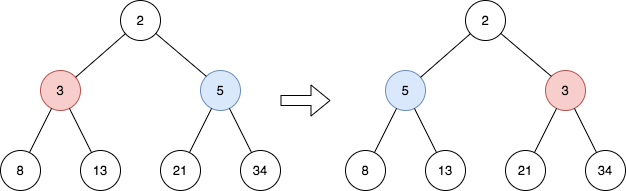
输入：root = [2,3,5,8,13,21,34]
输出：[2,5,3,8,13,21,34]
解释：
这棵树只有一个奇数层。
在第 1 层的节点分别是 3、5 ，反转后为 5、3 。

示例 2：

输入：root = [7,13,11]
输出：[7,11,13]
解释： 
在第 1 层的节点分别是 13、11 ，反转后为 11、13 。

示例 3：

输入：root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
输出：[0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
解释：奇数层由非零值组成。
在第 1 层的节点分别是 1、2 ，反转后为 2、1 。
在第 3 层的节点分别是 1、1、1、1、2、2、2、2 ，反转后为 2、2、2、2、1、1、1、1 。

 

提示：

  • 树中的节点数目在范围 [1, 214] 内
  • 0 <= Node.val <= 105
  • root 是一棵 完美 二叉树

解法

方法一：BFS

BFS 遍历二叉树，遍历到奇数层时，反转该层节点的值。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为二叉树的节点个数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def reverseOddLevels(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        q = deque([root])
        i = 0
        while q:
            t = []
            for _ in range(len(q)):
                node = q.popleft()
                if i & 1:
                    t.append(node)
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            if t:
                j, k = 0, len(t) - 1
                while j < k:
                    t[j].val, t[k].val = t[k].val, t[j].val
                    j, k = j + 1, k - 1
            i += 1
        return root

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode reverseOddLevels(TreeNode root) {
        Deque<TreeNode> q = new ArrayDeque<>();
        q.offer(root);
        int i = 0;
        while (!q.isEmpty()) {
            List<TreeNode> t = new ArrayList<>();
            for (int n = q.size(); n > 0; --n) {
                TreeNode node = q.pollFirst();
                if (i % 2 == 1) {
                    t.add(node);
                }
                if (node.left != null) {
                    q.offer(node.left);
                }
                if (node.right != null) {
                    q.offer(node.right);
                }
            }
            if (!t.isEmpty()) {
                int j = 0, k = t.size() - 1;
                for (; j < k; ++j, --k) {
                    int v = t.get(j).val;
                    t.get(j).val = t.get(k).val;
                    t.get(k).val = v;
                }
            }
            ++i;
        }
        return root;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* reverseOddLevels(TreeNode* root) {
        queue<TreeNode*> q{{root}};
        int i = 0;
        vector<TreeNode*> t;
        while (!q.empty()) {
            t.clear();
            for (int n = q.size(); n; --n) {
                TreeNode* node = q.front();
                q.pop();
                if (i & 1) {
                    t.push_back(node);
                }
                if (node->left) {
                    q.push(node->left);
                }
                if (node->right) {
                    q.push(node->right);
                }
            }
            if (t.size()) {
                int j = 0, k = t.size() - 1;
                for (; j < k; ++j, --k) {
                    int v = t[j]->val;
                    t[j]->val = t[k]->val;
                    t[k]->val = v;
                }
            }
            ++i;
        }
        return root;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func reverseOddLevels(root *TreeNode) *TreeNode {
	q := []*TreeNode{root}
	i := 0
	for len(q) > 0 {
		t := []*TreeNode{}
		for n := len(q); n > 0; n-- {
			node := q[0]
			q = q[1:]
			if i%2 == 1 {
				t = append(t, node)
			}
			if node.Left != nil {
				q = append(q, node.Left)
			}
			if node.Right != nil {
				q = append(q, node.Right)
			}
		}
		if len(t) > 0 {
			j, k := 0, len(t)-1
			for ; j < k; j, k = j+1, k-1 {
				v := t[j].Val
				t[j].Val = t[k].Val
				t[k].Val = v
			}
		}
		i++
	}
	return root
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function reverseOddLevels(root: TreeNode | null): TreeNode | null {
    const queue = [root];
    let d = 0;
    while (queue.length !== 0) {
        const n = queue.length;
        const t: TreeNode[] = [];
        for (let i = 0; i < n; i++) {
            const node = queue.shift();
            if (d % 2 == 1) {
                t.push(node);
            }
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
        const m = t.length;
        for (let i = 0; i < m >> 1; i++) {
            [t[i].val, t[m - 1 - i].val] = [t[m - 1 - i].val, t[i].val];
        }
        d++;
    }
    return root;
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
use std::collections::VecDeque;
impl Solution {
    fn create_tree(vals: &Vec<Vec<i32>>, i: usize, j: usize) -> Option<Rc<RefCell<TreeNode>>> {
        if i == vals.len() {
            return None;
        }
        Some(Rc::new(RefCell::new(TreeNode {
            val: vals[i][j],
            left: Self::create_tree(vals, i + 1, j * 2),
            right: Self::create_tree(vals, i + 1, j * 2 + 1),
        })))
    }

    pub fn reverse_odd_levels(
        root: Option<Rc<RefCell<TreeNode>>>,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        let mut queue = VecDeque::new();
        queue.push_back(root);
        let mut d = 0;
        let mut vals = Vec::new();
        while !queue.is_empty() {
            let mut val = Vec::new();
            for _ in 0..queue.len() {
                let mut node = queue.pop_front().unwrap();
                let mut node = node.as_mut().unwrap().borrow_mut();
                val.push(node.val);
                if node.left.is_some() {
                    queue.push_back(node.left.take());
                }
                if node.right.is_some() {
                    queue.push_back(node.right.take());
                }
            }
            if d % 2 == 1 {
                val.reverse();
            }
            vals.push(val);
            d += 1;
        }
        Self::create_tree(&vals, 0, 0)
    }
}

...