README.md

2374. 边积分最高的节点

English Version

题目描述

给你一个有向图，图中有 n 个节点，节点编号从 0 到 n - 1 ，其中每个节点都 恰有一条 出边。

图由一个下标从 0 开始、长度为 n 的整数数组 edges 表示，其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的 有向 边。

节点 i 的 边积分 定义为：所有存在一条指向节点 i 的边的节点的 编号 总和。

返回 边积分 最高的节点。如果多个节点的 边积分 相同，返回编号 最小 的那个。

 

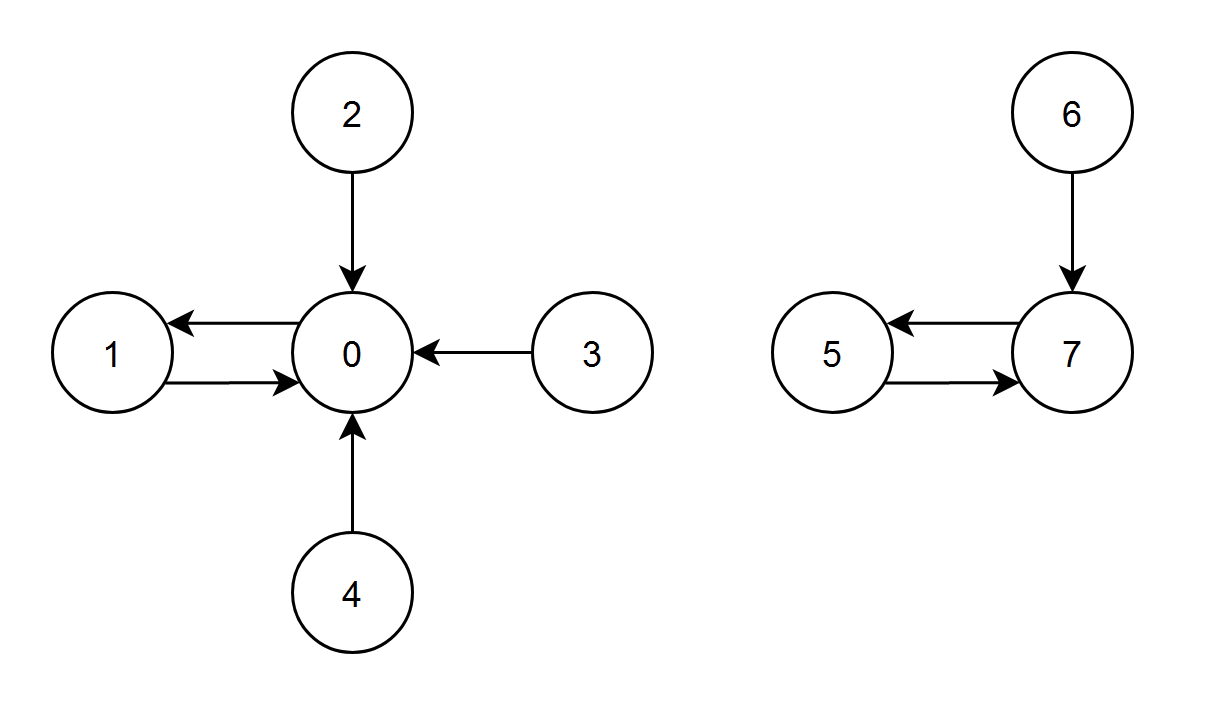
示例 1：

输入：edges = [1,0,0,0,0,7,7,5]
输出：7
解释：
- 节点 1、2、3 和 4 都有指向节点 0 的边，节点 0 的边积分等于 1 + 2 + 3 + 4 = 10 。
- 节点 0 有一条指向节点 1 的边，节点 1 的边积分等于 0 。
- 节点 7 有一条指向节点 5 的边，节点 5 的边积分等于 7 。
- 节点 5 和 6 都有指向节点 7 的边，节点 7 的边积分等于 5 + 6 = 11 。
节点 7 的边积分最高，所以返回 7 。

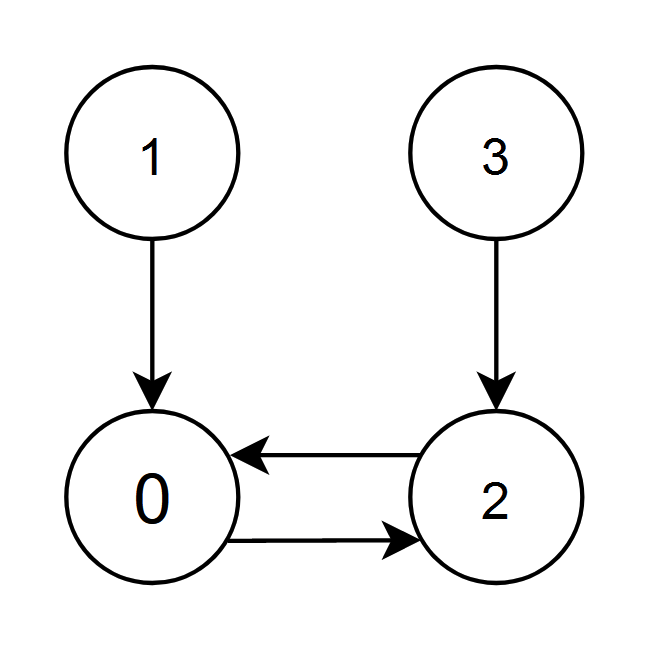
示例 2：

输入：edges = [2,0,0,2]
输出：0
解释：
- 节点 1 和 2 都有指向节点 0 的边，节点 0 的边积分等于 1 + 2 = 3 。
- 节点 0 和 3 都有指向节点 2 的边，节点 2 的边积分等于 0 + 3 = 3 。
节点 0 和 2 的边积分都是 3 。由于节点 0 的编号更小，返回 0 。

 

提示：

• n == edges.length
• 2 <= n <= 105
• 0 <= edges[i] < n
• edges[i] != i

解法

方法一：遍历计数

定义 $cnt$，其中每个元素 $cnt[i]$ 表示到节点 $i$ 的所有节点编号之和。

最后找出 $cnt$ 中最大的元素 $cnt[i]$，返回 $i$。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是节点的数量。

Python3

class Solution:
    def edgeScore(self, edges: List[int]) -> int:
        cnt = Counter()
        for i, v in enumerate(edges):
            cnt[v] += i
        ans = 0
        for i in range(len(edges)):
            if cnt[ans] < cnt[i]:
                ans = i
        return ans

Java

class Solution {
    public int edgeScore(int[] edges) {
        int n = edges.length;
        long[] cnt = new long[n];
        for (int i = 0; i < n; ++i) {
            cnt[edges[i]] += i;
        }
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            if (cnt[ans] < cnt[i]) {
                ans = i;
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int edgeScore(vector<int>& edges) {
        int n = edges.size();
        vector<long long> cnt(n);
        for (int i = 0; i < n; ++i) {
            cnt[edges[i]] += i;
        }
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            if (cnt[ans] < cnt[i]) {
                ans = i;
            }
        }
        return ans;
    }
};

Go

func edgeScore(edges []int) int {
	n := len(edges)
	cnt := make([]int, n)
	for i, v := range edges {
		cnt[v] += i
	}
	ans := 0
	for i, v := range cnt {
		if cnt[ans] < v {
			ans = i
		}
	}
	return ans
}

TypeScript

function edgeScore(edges: number[]): number {
    const n = edges.length;
    const sum = new Array(n).fill(0);
    for (let i = 0; i < n; i++) {
        sum[edges[i]] += i;
    }
    let res = 0;
    for (let i = 0; i < n; i++) {
        if (sum[res] < sum[i]) {
            res = i;
        }
    }
    return res;
}

...