README.md

2304. 网格中的最小路径代价

English Version

题目描述

给你一个下标从 0 开始的整数矩阵 grid ，矩阵大小为 m x n ，由从 0 到 m * n - 1 的不同整数组成。你可以在此矩阵中，从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ，且满足 x < m - 1 ，你可以移动到 (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1) 中的任何一个单元格。注意： 在最后一行中的单元格不能触发移动。

每次可能的移动都需要付出对应的代价，代价用一个下标从 0 开始的二维数组 moveCost 表示，该数组大小为 (m * n) x n ，其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。

grid 一条路径的代价是：所有路径经过的单元格的 值之和 加上 所有移动的 代价之和 。从 第一行 任意单元格出发，返回到达 最后一行 任意单元格的最小路径代价。

 

示例 1：

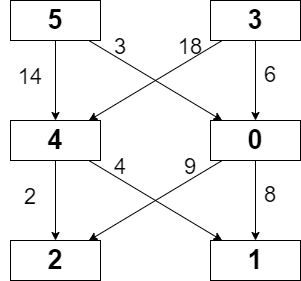
输入：grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
输出：17
解释：最小代价的路径是 5 -> 0 -> 1 。
- 路径途经单元格值之和 5 + 0 + 1 = 6 。
- 从 5 移动到 0 的代价为 3 。
- 从 0 移动到 1 的代价为 8 。
路径总代价为 6 + 3 + 8 = 17 。

示例 2：

输入：grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
输出：6
解释：
最小代价的路径是 2 -> 3 。 
- 路径途经单元格值之和 2 + 3 = 5 。 
- 从 2 移动到 3 的代价为 1 。 
路径总代价为 5 + 1 = 6 。

 

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 50
• grid 由从 0 到 m * n - 1 的不同整数组成
• moveCost.length == m * n
• moveCost[i].length == n
• 1 <= moveCost[i][j] <= 100

解法

方法一：递推

Python3

class Solution:
    def minPathCost(self, grid: List[List[int]], moveCost: List[List[int]]) -> int:
        n = len(grid[0])
        f = [0] * n
        for i, row in enumerate(grid):
            g = [0] * n
            for j, v in enumerate(row):
                g[j] = v
                t = inf
                if i:
                    for k, x in enumerate(grid[i - 1]):
                        t = min(t, f[k] + moveCost[x][j])
                if t != inf:
                    g[j] += t
            f = g
        return min(f)

Java

class Solution {
    public int minPathCost(int[][] grid, int[][] moveCost) {
        int m = grid.length, n = grid[0].length;
        int inf = Integer.MAX_VALUE;
        int[] f = new int[n];
        for (int i = 0; i < m; ++i) {
            int[] g = new int[n];
            for (int j = 0; j < n; ++j) {
                g[j] = grid[i][j];
                int t = inf;
                if (i > 0) {
                    for (int k = 0; k < n; ++k) {
                        t = Math.min(t, f[k] + moveCost[grid[i - 1][k]][j]);
                    }
                }
                if (t != inf) {
                    g[j] += t;
                }
            }
            f = g;
        }
        int ans = inf;
        for (int v : f) {
            ans = Math.min(ans, v);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
        int m = grid.size(), n = grid[0].size();
        int inf = INT_MAX;
        vector<int> f(n);
        for (int i = 0; i < m; ++i) {
            vector<int> g(n);
            for (int j = 0; j < n; ++j) {
                g[j] = grid[i][j];
                int t = inf;
                if (i) {
                    for (int k = 0; k < n; ++k) {
                        t = min(t, f[k] + moveCost[grid[i - 1][k]][j]);
                    }
                }
                if (t != inf) g[j] += t;
            }
            f = g;
        }
        return *min_element(f.begin(), f.end());
    }
};

Go

func minPathCost(grid [][]int, moveCost [][]int) int {
	n := len(grid[0])
	inf := 0x3f3f3f3f
	f := make([]int, n)
	for i, row := range grid {
		g := make([]int, n)
		for j, v := range row {
			g[j] = v
			t := inf
			if i > 0 {
				for k := 0; k < n; k++ {
					t = min(t, f[k]+moveCost[grid[i-1][k]][j])
				}
			}
			if t != inf {
				g[j] += t
			}
		}
		f = g
	}
	ans := inf
	for _, v := range f {
		ans = min(ans, v)
	}
	return ans
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

Rust

impl Solution {
    pub fn min_path_cost(grid: Vec<Vec<i32>>, move_cost: Vec<Vec<i32>>) -> i32 {
        let (m, n) = (grid.len(), grid[0].len());
        let mut dp = vec![0; n];
        for i in 0..m - 1 {
            let mut counter = vec![i32::MAX; n];
            for j in 0..n {
                let val = grid[i][j];
                for k in 0..n {
                    counter[k] = counter[k].min(val + move_cost[val as usize][k] + dp[j]);
                }
            }
            for j in 0..n {
                dp[j] = counter[j];
            }
        }
        let mut res = i32::MAX;
        for i in 0..n {
            res = res.min(dp[i] + grid[m - 1][i]);
        }
        res
    }
}

TypeScript

function minPathCost(grid: number[][], moveCost: number[][]): number {
    const m = grid.length,
        n = grid[0].length;
    let pre = grid[0].slice();
    for (let i = 1; i < m; i++) {
        let next = new Array(n);
        for (let j = 0; j < n; j++) {
            const key = grid[i - 1][j];
            for (let k = 0; k < n; k++) {
                let sum = pre[j] + moveCost[key][k] + grid[i][k];
                if (j == 0 || next[k] > sum) {
                    next[k] = sum;
                }
            }
        }
        pre = next;
    }
    return Math.min(...pre);
}

...