There is an undirected graph with n nodes, numbered from 0 to n - 1.
You are given a 0-indexed integer array scores of length n where scores[i] denotes the score of node i. You are also given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.
A node sequence is valid if it meets the following conditions:
- There is an edge connecting every pair of adjacent nodes in the sequence.
- No node appears more than once in the sequence.
The score of a node sequence is defined as the sum of the scores of the nodes in the sequence.
Return the maximum score of a valid node sequence with a length of 4. If no such sequence exists, return -1.
Example 1:
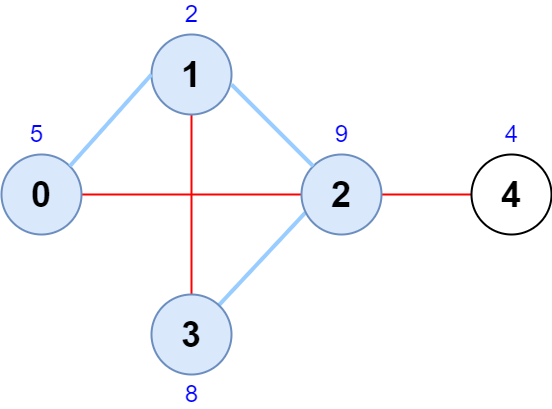
Input: scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]] Output: 24 Explanation: The figure above shows the graph and the chosen node sequence [0,1,2,3]. The score of the node sequence is 5 + 2 + 9 + 8 = 24. It can be shown that no other node sequence has a score of more than 24. Note that the sequences [3,1,2,0] and [1,0,2,3] are also valid and have a score of 24. The sequence [0,3,2,4] is not valid since no edge connects nodes 0 and 3.
Example 2:
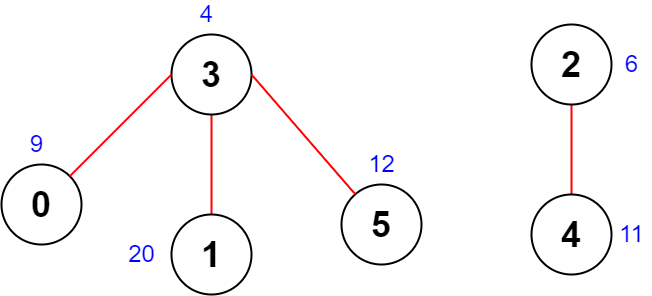
Input: scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]] Output: -1 Explanation: The figure above shows the graph. There are no valid node sequences of length 4, so we return -1.
Constraints:
n == scores.length4 <= n <= 5 * 1041 <= scores[i] <= 1080 <= edges.length <= 5 * 104edges[i].length == 20 <= ai, bi <= n - 1ai != bi- There are no duplicate edges.
class Solution:
def maximumScore(self, scores: List[int], edges: List[List[int]]) -> int:
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
for k in g.keys():
g[k] = nlargest(3, g[k], key=lambda x: scores[x])
ans = -1
for a, b in edges:
for c in g[a]:
for d in g[b]:
if b != c != d != a:
t = scores[a] + scores[b] + scores[c] + scores[d]
ans = max(ans, t)
return ansclass Solution {
public int maximumScore(int[] scores, int[][] edges) {
int n = scores.length;
List<Integer>[] g = new List[n];
for (int i = 0; i < n; ++i) {
g[i] = new ArrayList<>();
}
for (int[] e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
for (int i = 0; i < n; ++i) {
g[i].sort((a, b) -> scores[b] - scores[a]);
g[i] = g[i].subList(0, Math.min(3, g[i].size()));
}
int ans = -1;
for (int[] e : edges) {
int a = e[0], b = e[1];
for (int c : g[a]) {
for (int d : g[b]) {
if (c != b && c != d && a != d) {
int t = scores[a] + scores[b] + scores[c] + scores[d];
ans = Math.max(ans, t);
}
}
}
}
return ans;
}
}