README_EN.md

2132. Stamping the Grid

中文文档

Description

You are given an m x n binary matrix grid where each cell is either 0 (empty) or 1 (occupied).

You are then given stamps of size stampHeight x stampWidth. We want to fit the stamps such that they follow the given restrictions and requirements:

1. Cover all the empty cells.
2. Do not cover any of the occupied cells.
3. We can put as many stamps as we want.
4. Stamps can overlap with each other.
5. Stamps are not allowed to be rotated.
6. Stamps must stay completely inside the grid.

Return true if it is possible to fit the stamps while following the given restrictions and requirements. Otherwise, return false.

 

Example 1:

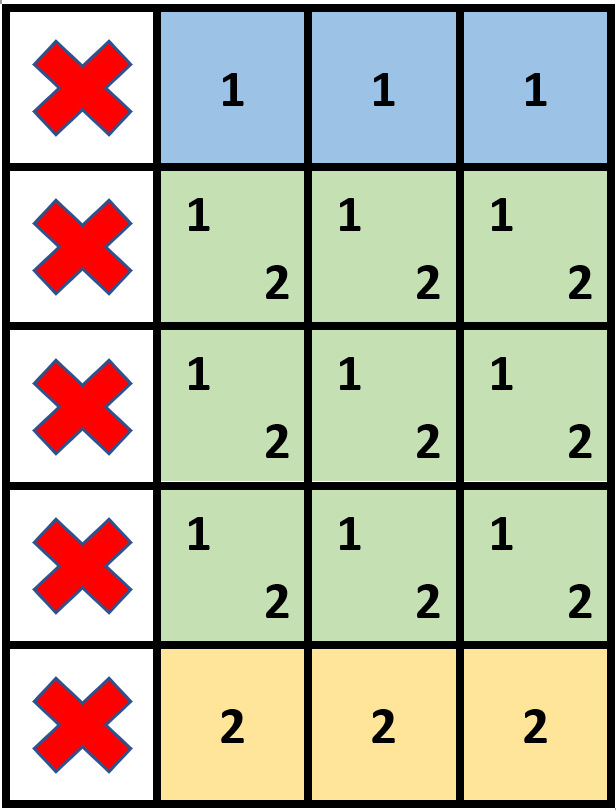
Input: grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
Output: true
Explanation: We have two overlapping stamps (labeled 1 and 2 in the image) that are able to cover all the empty cells.

Example 2:

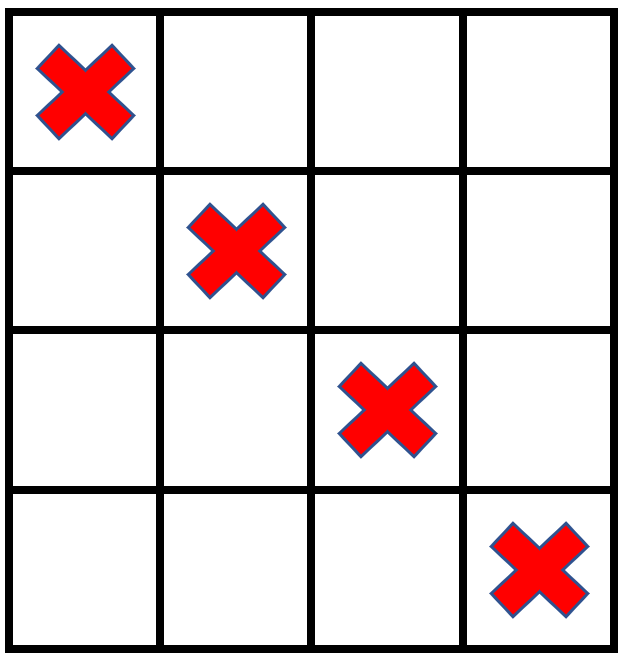
Input: grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 
Output: false 
Explanation: There is no way to fit the stamps onto all the empty cells without the stamps going outside the grid.

 

Constraints:

• m == grid.length
• n == grid[r].length
• 1 <= m, n <= 105
• 1 <= m * n <= 2 * 105
• grid[r][c] is either 0 or 1.
• 1 <= stampHeight, stampWidth <= 105

Solutions

Python3

class Solution:
    def possibleToStamp(
        self, grid: List[List[int]], stampHeight: int, stampWidth: int
    ) -> bool:
        m, n = len(grid), len(grid[0])
        s = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + v

        d = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                if v == 0:
                    x, y = i + stampHeight, j + stampWidth
                    if x <= m and y <= n and s[x][y] - s[x][j] - s[i][y] + s[i][j] == 0:
                        d[i][j] += 1
                        d[i][y] -= 1
                        d[x][j] -= 1
                        d[x][y] += 1

        cnt = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                cnt[i + 1][j + 1] = cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j]
                if v == 0 and cnt[i + 1][j + 1] == 0:
                    return False
        return True

Java

class Solution {
    public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) {
        int m = grid.length, n = grid[0].length;
        int[][] s = new int[m + 1][n + 1];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
            }
        }
        int[][] d = new int[m + 1][n + 1];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 0) {
                    int x = i + stampHeight, y = j + stampWidth;
                    if (x <= m && y <= n && s[x][y] - s[x][j] - s[i][y] + s[i][j] == 0) {
                        d[i][j]++;
                        d[i][y]--;
                        d[x][j]--;
                        d[x][y]++;
                    }
                }
            }
        }
        int[][] cnt = new int[m + 1][n + 1];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                cnt[i + 1][j + 1] = cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j];
                if (grid[i][j] == 0 && cnt[i + 1][j + 1] == 0) {
                    return false;
                }
            }
        }
        return true;
    }
}

C++

class Solution {
public:
    bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> s(m + 1, vector<int>(n + 1));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
            }
        }
        vector<vector<int>> d(m + 1, vector<int>(n + 1));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j]) continue;
                int x = i + stampHeight, y = j + stampWidth;
                if (x <= m && y <= n && s[x][y] - s[i][y] - s[x][j] + s[i][j] == 0) {
                    d[i][j]++;
                    d[x][j]--;
                    d[i][y]--;
                    d[x][y]++;
                }
            }
        }
        vector<vector<int>> cnt(m + 1, vector<int>(n + 1));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                cnt[i + 1][j + 1] = cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j];
                if (grid[i][j] == 0 && cnt[i + 1][j + 1] == 0) return false;
            }
        }
        return true;
    }
};

Go

func possibleToStamp(grid [][]int, stampHeight int, stampWidth int) bool {
	m, n := len(grid), len(grid[0])
	s := make([][]int, m+1)
	d := make([][]int, m+1)
	cnt := make([][]int, m+1)
	for i := range s {
		s[i] = make([]int, n+1)
		d[i] = make([]int, n+1)
		cnt[i] = make([]int, n+1)
	}
	for i, row := range grid {
		for j, v := range row {
			s[i+1][j+1] = s[i+1][j] + s[i][j+1] - s[i][j] + v
		}
	}
	for i, row := range grid {
		for j, v := range row {
			if v == 0 {
				x, y := i+stampHeight, j+stampWidth
				if x <= m && y <= n && s[x][y]-s[i][y]-s[x][j]+s[i][j] == 0 {
					d[i][j]++
					d[i][y]--
					d[x][j]--
					d[x][y]++
				}
			}
		}
	}
	for i, row := range grid {
		for j, v := range row {
			cnt[i+1][j+1] = cnt[i+1][j] + cnt[i][j+1] - cnt[i][j] + d[i][j]
			if v == 0 && cnt[i+1][j+1] == 0 {
				return false
			}
		}
	}
	return true
}

JavaScript

/**
 * @param {number[][]} grid
 * @param {number} stampHeight
 * @param {number} stampWidth
 * @return {boolean}
 */
var possibleToStamp = function (grid, stampHeight, stampWidth) {
    const m = grid.length;
    const n = grid[0].length;
    let s = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
    let d = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
    let cnt = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
        }
    }
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (grid[i][j] == 0) {
                let [x, y] = [i + stampHeight, j + stampWidth];
                if (
                    x <= m &&
                    y <= n &&
                    s[x][y] - s[i][y] - s[x][j] + s[i][j] == 0
                ) {
                    d[i][j]++;
                    d[i][y]--;
                    d[x][j]--;
                    d[x][y]++;
                }
            }
        }
    }
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            cnt[i + 1][j + 1] =
                cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j];
            if (grid[i][j] == 0 && cnt[i + 1][j + 1] == 0) {
                return false;
            }
        }
    }
    return true;
};

TypeScript

...