在一个无限的 x 坐标轴上,有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ,其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ,每个 positioni 互不相同 。
另给你两个整数 startPos 和 k 。最初,你位于 startPos 。从任何位置,你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ,就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置,都会摘掉全部的水果,水果也将从该位置消失(不会再生)。
返回你可以摘到水果的 最大总数 。
示例 1:
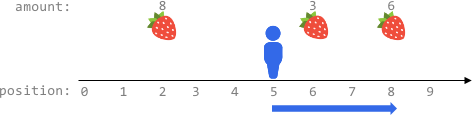
输入:fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4 输出:9 解释: 最佳路线为: - 向右移动到位置 6 ,摘到 3 个水果 - 向右移动到位置 8 ,摘到 6 个水果 移动 3 步,共摘到 3 + 6 = 9 个水果
示例 2:
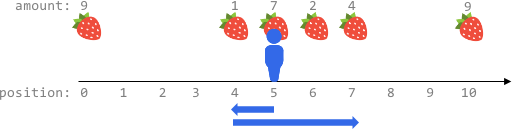
输入:fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4 输出:14 解释: 可以移动最多 k = 4 步,所以无法到达位置 0 和位置 10 。 最佳路线为: - 在初始位置 5 ,摘到 7 个水果 - 向左移动到位置 4 ,摘到 1 个水果 - 向右移动到位置 6 ,摘到 2 个水果 - 向右移动到位置 7 ,摘到 4 个水果 移动 1 + 3 = 4 步,共摘到 7 + 1 + 2 + 4 = 14 个水果
示例 3:
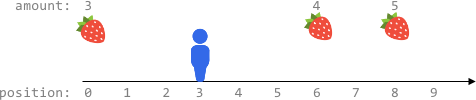
输入:fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2 输出:0 解释: 最多可以移动 k = 2 步,无法到达任一有水果的地方
提示:
1 <= fruits.length <= 105fruits[i].length == 20 <= startPos, positioni <= 2 * 105- 对于任意
i > 0,positioni-1 < positioni均成立(下标从 0 开始计数) 1 <= amounti <= 1040 <= k <= 2 * 105
在满足最多走 k 步的条件下,只需要确定能到达的左右端点即可。
首先从左边开始,找到能到达的最左端点,并把从此处开始到 startPos 的所有水果累加,此过程中依次入队。
然后开始确定右端点,在确定右端点的时候,检查左右端点之间的步数,若超过 k,则要减去左端点的值,同时出队。此过程中更新最大值 ans 即可。
class Solution:
def maxTotalFruits(self, fruits: List[List[int]], startPos: int, k: int) -> int:
q = deque()
i, n = 0, len(fruits)
ans = 0
while i < n and fruits[i][0] <= startPos:
if startPos - fruits[i][0] <= k:
ans += fruits[i][1]
q.append(fruits[i])
i += 1
t = ans
while i < n and fruits[i][0] - startPos <= k:
while (
q
and q[0][0] < startPos
and fruits[i][0]
- q[0][0]
+ min(startPos - q[0][0], fruits[i][0] - startPos)
> k
):
t -= q[0][1]
q.popleft()
t += fruits[i][1]
ans = max(ans, t)
i += 1
return ansclass Solution {
public int maxTotalFruits(int[][] fruits, int startPos, int k) {
Deque<int[]> q = new ArrayDeque<>();
int i = 0, n = fruits.length;
int ans = 0;
while (i < n && fruits[i][0] <= startPos) {
if (startPos - fruits[i][0] <= k) {
ans += fruits[i][1];
q.offerLast(fruits[i]);
}
++i;
}
int t = ans;
while (i < n && fruits[i][0] - startPos <= k) {
while (!q.isEmpty() && q.peekFirst()[0] < startPos
&& fruits[i][0] - q.peekFirst()[0]
+ Math.min(startPos - q.peekFirst()[0], fruits[i][0] - startPos)
> k) {
t -= q.pollFirst()[1];
}
t += fruits[i][1];
ans = Math.max(ans, t);
++i;
}
return ans;
}
}class Solution {
public:
int maxTotalFruits(vector<vector<int>>& fruits, int startPos, int k) {
queue<vector<int>> q;
int i = 0, n = fruits.size();
int ans = 0;
while (i < n && fruits[i][0] <= startPos) {
if (startPos - fruits[i][0] <= k) {
ans += fruits[i][1];
q.push(fruits[i]);
}
++i;
}
int t = ans;
while (i < n && fruits[i][0] - startPos <= k) {
while (!q.empty() && q.front()[0] < startPos && fruits[i][0] - q.front()[0] + min(startPos - q.front()[0], fruits[i][0] - startPos) > k) {
t -= q.front()[1];
q.pop();
}
t += fruits[i][1];
ans = max(ans, t);
++i;
}
return ans;
}
};func maxTotalFruits(fruits [][]int, startPos int, k int) int {
var q [][]int
i, n := 0, len(fruits)
ans := 0
for i < n && fruits[i][0] <= startPos {
if startPos-fruits[i][0] <= k {
ans += fruits[i][1]
q = append(q, fruits[i])
}
i++
}
t := ans
for i < n && fruits[i][0]-startPos <= k {
for len(q) > 0 && q[0][0] < startPos && fruits[i][0]-q[0][0]+min(startPos-q[0][0], fruits[i][0]-startPos) > k {
t -= q[0][1]
q = q[1:]
}
t += fruits[i][1]
ans = max(ans, t)
i++
}
return ans
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(a, b int) int {
if a < b {
return a
}
return b
}