Skip to content

Latest commit

 

History

History
187 lines (148 loc) · 5.72 KB

README.md

File metadata and controls

187 lines (148 loc) · 5.72 KB

2090. 半径为 k 的子数组平均值

English Version

题目描述

给你一个下标从 0 开始的数组 nums ，数组中有 n 个整数，另给你一个整数 k 。

半径为 k 的子数组平均值 是指：nums 中一个以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值，即下标在 i - k 和 i + k 范围（含 i - k 和 i + k）内所有元素的平均值。如果在下标 i 前或后不足 k 个元素，那么 半径为 k 的子数组平均值 是 -1 。

构建并返回一个长度为 n 的数组 avgs ，其中 avgs[i] 是以下标 i 为中心的子数组的 半径为 k 的子数组平均值 。

x 个元素的 平均值 是 x 个元素相加之和除以 x ，此时使用截断式 整数除法 ，即需要去掉结果的小数部分。

  • 例如，四个元素 2、3、1 和 5 的平均值是 (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75，截断后得到 2 。

 

示例 1：

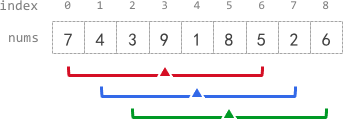
输入：nums = [7,4,3,9,1,8,5,2,6], k = 3
输出：[-1,-1,-1,5,4,4,-1,-1,-1]
解释：
- avg[0]、avg[1] 和 avg[2] 是 -1 ，因为在这几个下标前的元素数量都不足 k 个。
- 中心为下标 3 且半径为 3 的子数组的元素总和是：7 + 4 + 3 + 9 + 1 + 8 + 5 = 37 。
  使用截断式 整数除法，avg[3] = 37 / 7 = 5 。
- 中心为下标 4 的子数组，avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4 。
- 中心为下标 5 的子数组，avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4 。
- avg[6]、avg[7] 和 avg[8] 是 -1 ，因为在这几个下标后的元素数量都不足 k 个。

示例 2：

输入：nums = [100000], k = 0
输出：[100000]
解释：
- 中心为下标 0 且半径 0 的子数组的元素总和是：100000 。
  avg[0] = 100000 / 1 = 100000 。

示例 3：

输入：nums = [8], k = 100000
输出：[-1]
解释：
- avg[0] 是 -1 ，因为在下标 0 前后的元素数量均不足 k 。

 

提示：

  • n == nums.length
  • 1 <= n <= 105
  • 0 <= nums[i], k <= 105

解法

前缀和。

Python3

class Solution:
    def getAverages(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        presum = [0] * (n + 1)
        for i in range(n):
            presum[i + 1] = presum[i] + nums[i]
        return [
            -1
            if i - k < 0 or i + k >= n
            else (presum[i + k + 1] - presum[i - k]) // (k * 2 + 1)
            for i in range(n)
        ]

Java

class Solution {
    public int[] getAverages(int[] nums, int k) {
        int n = nums.length;
        long[] presum = new long[n + 1];
        for (int i = 0; i < n; ++i) {
            presum[i + 1] = presum[i] + nums[i];
        }
        int[] ans = new int[n];
        for (int i = 0; i < n; ++i) {
            if (i - k < 0 || i + k >= n) {
                ans[i] = -1;
            } else {
                ans[i] = (int) ((presum[i + k + 1] - presum[i - k]) / (k * 2 + 1));
            }
        }
        return ans;
    }
}

TypeScript

function getAverages(nums: number[], k: number): number[] {
    const n = nums.length;
    const l = 2 * k + 1;
    let sum = 0;
    let ans = new Array(n).fill(-1);
    for (let i = 0; i < n; i++) {
        sum += nums[i];
        let shiftIndex = i - l;
        if (shiftIndex > -1) {
            sum -= nums[shiftIndex];
        }
        if (i + 1 >= l) {
            ans[i - k] = Math.floor(sum / l);
        }
    }
    return ans;
}

C++

class Solution {
public:
    vector<int> getAverages(vector<int>& nums, int k) {
        int n = nums.size();
        vector<long long> presum(n + 1);
        for (int i = 0; i < n; ++i) presum[i + 1] = presum[i] + nums[i];
        vector<int> ans(n, -1);
        for (int i = 0; i < n; ++i)
            if (i - k >= 0 && i + k < n)
                ans[i] = (presum[i + k + 1] - presum[i - k]) * 1ll / (k * 2 + 1);
        return ans;
    }
};

Go

func getAverages(nums []int, k int) []int {
	n := len(nums)
	presum := make([]int64, n+1)
	for i, num := range nums {
		presum[i+1] = presum[i] + int64(num)
	}
	var ans []int
	for i := 0; i < n; i++ {
		if i-k < 0 || i+k >= n {
			ans = append(ans, -1)
		} else {
			ans = append(ans, int((presum[i+k+1]-presum[i-k])/int64(k*2+1)))
		}
	}
	return ans
}

...