README.md

2017. 网格游戏

English Version

题目描述

给你一个下标从 0 开始的二维数组 grid ，数组大小为 2 x n ，其中 grid[r][c] 表示矩阵中 (r, c) 位置上的点数。现在有两个机器人正在矩阵上参与一场游戏。

两个机器人初始位置都是 (0, 0) ，目标位置是 (1, n-1) 。每个机器人只会 向右 ((r, c) 到 (r, c + 1)) 或 向下 ((r, c) 到 (r + 1, c)) 。

游戏开始，第一个 机器人从 (0, 0) 移动到 (1, n-1) ，并收集路径上单元格的全部点数。对于路径上所有单元格 (r, c) ，途经后 grid[r][c] 会重置为 0 。然后，第二个 机器人从 (0, 0) 移动到 (1, n-1) ，同样收集路径上单元的全部点数。注意，它们的路径可能会存在相交的部分。

第一个 机器人想要打击竞争对手，使 第二个 机器人收集到的点数 最小化 。与此相对，第二个 机器人想要 最大化 自己收集到的点数。两个机器人都发挥出自己的 最佳水平 的前提下，返回 第二个 机器人收集到的 点数 。

 

示例 1：

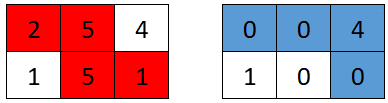
输入：grid = [[2,5,4],[1,5,1]]
输出：4
解释：第一个机器人的最佳路径如红色所示，第二个机器人的最佳路径如蓝色所示。
第一个机器人访问过的单元格将会重置为 0 。
第二个机器人将会收集到 0 + 0 + 4 + 0 = 4 个点。

示例 2：

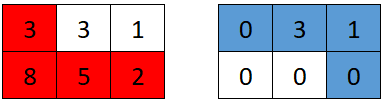
输入：grid = [[3,3,1],[8,5,2]]
输出：4
解释：第一个机器人的最佳路径如红色所示，第二个机器人的最佳路径如蓝色所示。 
第一个机器人访问过的单元格将会重置为 0 。
第二个机器人将会收集到 0 + 3 + 1 + 0 = 4 个点。

示例 3：

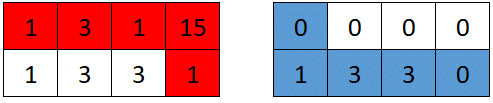
输入：grid = [[1,3,1,15],[1,3,3,1]]
输出：7
解释：第一个机器人的最佳路径如红色所示，第二个机器人的最佳路径如蓝色所示。
第一个机器人访问过的单元格将会重置为 0 。
第二个机器人将会收集到 0 + 1 + 3 + 3 + 0 = 7 个点。

 

提示：

• grid.length == 2
• n == grid[r].length
• 1 <= n <= 5 * 104
• 1 <= grid[r][c] <= 105

解法

Python3

class Solution:
    def gridGame(self, grid: List[List[int]]) -> int:
        ans = inf
        s1, s2 = sum(grid[0]), 0
        for j, v in enumerate(grid[0]):
            s1 -= v
            ans = min(ans, max(s1, s2))
            s2 += grid[1][j]
        return ans

Java

class Solution {
    public long gridGame(int[][] grid) {
        long ans = Long.MAX_VALUE;
        long s1 = 0, s2 = 0;
        for (int v : grid[0]) {
            s1 += v;
        }
        int n = grid[0].length;
        for (int j = 0; j < n; ++j) {
            s1 -= grid[0][j];
            ans = Math.min(ans, Math.max(s1, s2));
            s2 += grid[1][j];
        }
        return ans;
    }
}

C++

using ll = long long;

class Solution {
public:
    long long gridGame(vector<vector<int>>& grid) {
        ll ans = LONG_MAX;
        int n = grid[0].size();
        ll s1 = 0, s2 = 0;
        for (int& v : grid[0]) s1 += v;
        for (int j = 0; j < n; ++j) {
            s1 -= grid[0][j];
            ans = min(ans, max(s1, s2));
            s2 += grid[1][j];
        }
        return ans;
    }
};

Go

func gridGame(grid [][]int) int64 {
	ans := math.MaxInt64
	s1, s2 := 0, 0
	for _, v := range grid[0] {
		s1 += v
	}
	for j, v := range grid[0] {
		s1 -= v
		ans = min(ans, max(s1, s2))
		s2 += grid[1][j]
	}
	return int64(ans)
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

...