README_EN.md

1791. Find Center of Star Graph

中文文档

Description

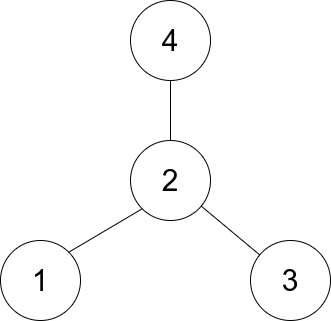
There is an undirected star graph consisting of n nodes labeled from 1 to n. A star graph is a graph where there is one center node and exactly n - 1 edges that connect the center node with every other node.

You are given a 2D integer array edges where each edges[i] = [ui, vi] indicates that there is an edge between the nodes ui and vi. Return the center of the given star graph.

 

Example 1:

Input: edges = [[1,2],[2,3],[4,2]]
Output: 2
Explanation: As shown in the figure above, node 2 is connected to every other node, so 2 is the center.

Example 2:

Input: edges = [[1,2],[5,1],[1,3],[1,4]]
Output: 1

 

Constraints:

• 3 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 1 <= ui, vi <= n
• ui != vi
• The given edges represent a valid star graph.

Solutions

Python3

class Solution:
    def findCenter(self, edges: List[List[int]]) -> int:
        return edges[0][0] if edges[0][0] in edges[1] else edges[0][1]

Java

class Solution {
    public int findCenter(int[][] edges) {
        int a = edges[0][0], b = edges[0][1];
        int c = edges[1][0], d = edges[1][1];
        return a == c || a == d ? a : b;
    }
}

TypeScript

function findCenter(edges: number[][]): number {
    for (let num of edges[0]) {
        if (edges[1].includes(num)) {
            return num;
        }
    }
}

C++

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        int a = edges[0][0], b = edges[0][1];
        int c = edges[1][0], d = edges[1][1];
        return a == c || a == d ? a : b;
    }
};

Go

func findCenter(edges [][]int) int {
	a, b := edges[0][0], edges[0][1]
	c, d := edges[1][0], edges[1][1]
	if a == c || a == d {
		return a
	}
	return b
}

Rust

impl Solution {
    pub fn find_center(edges: Vec<Vec<i32>>) -> i32 {
        if edges[0][0] == edges[1][0] || edges[0][0] == edges[1][1] {
            return edges[0][0];
        }
        edges[0][1]
    }
}

JavaScript

/**
 * @param {number[][]} edges
 * @return {number}
 */
var findCenter = function (edges) {
    const [a, b] = edges[0];
    const [c, d] = edges[1];
    return a == c || a == d ? a : b;
};

...