给你一个数组 pairs ,其中 pairs[i] = [xi, yi] ,并且满足:
pairs中没有重复元素xi < yi
令 ways 为满足下面条件的有根树的方案数:
- 树所包含的所有节点值都在
pairs中。 - 一个数对
[xi, yi]出现在pairs中 当且仅当xi是yi的祖先或者yi是xi的祖先。 - 注意:构造出来的树不一定是二叉树。
两棵树被视为不同的方案当存在至少一个节点在两棵树中有不同的父节点。
请你返回:
- 如果
ways == 0,返回0。 - 如果
ways == 1,返回1。 - 如果
ways > 1,返回2。
一棵 有根树 指的是只有一个根节点的树,所有边都是从根往外的方向。
我们称从根到一个节点路径上的任意一个节点(除去节点本身)都是该节点的 祖先 。根节点没有祖先。
示例 1:
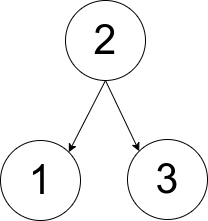
输入:pairs = [[1,2],[2,3]] 输出:1 解释:如上图所示,有且只有一个符合规定的有根树。
示例 2:
输入:pairs = [[1,2],[2,3],[1,3]] 输出:2 解释:有多个符合规定的有根树,其中三个如上图所示。
示例 3:
输入:pairs = [[1,2],[2,3],[2,4],[1,5]] 输出:0 解释:没有符合规定的有根树。
提示:
1 <= pairs.length <= 1051 <= xi < yi <= 500pairs中的元素互不相同。
题目性质:假设祖先节点为 x ,后代节点为 y ,则 x 在 pairs 中的出现次数一定大于等于 y 在 pairs 中的出现次数,且当等号成立时 x、y 可互换位置。
思路:
- 用邻接矩阵、邻接表存放 pairs。
- 将树中所有节点 nodes 按照出现的次数升序排列。设置 equal 标志,用来记录是否出现“次数相同”的祖孙节点,root 用来记录没有父节点的节点数。
- 遍历每个节点
nodes[i](记为 x),找出出现次数大于 x 的节点 y。如果 x 跟 y 构成祖孙关系,那么 y 的邻居 z 也需要构成祖孙关系。否则直接返回 0。
遍历结束,判断 root 的个数,若大于 1,说明不满足只有一个根节点,返回 0。若 equal 为真,说明存在可互换祖孙关系的节点对,返回 2;否则返回 1。
class Solution:
def checkWays(self, pairs: List[List[int]]) -> int:
g = [[False] * 510 for _ in range(510)]
v = defaultdict(list)
for x, y in pairs:
g[x][y] = g[y][x] = True
v[x].append(y)
v[y].append(x)
nodes = []
for i in range(510):
if v[i]:
nodes.append(i)
g[i][i] = True
nodes.sort(key=lambda x: len(v[x]))
equal = False
root = 0
for i, x in enumerate(nodes):
j = i + 1
while j < len(nodes) and not g[x][nodes[j]]:
j += 1
if j < len(nodes):
y = nodes[j]
if len(v[x]) == len(v[y]):
equal = True
for z in v[x]:
if not g[y][z]:
return 0
else:
root += 1
if root > 1:
return 0
return 2 if equal else 1class Solution {
public int checkWays(int[][] pairs) {
boolean[][] g = new boolean[510][510];
List<Integer>[] v = new List[510];
for (int i = 0; i < 510; ++i) {
v[i] = new ArrayList<>();
}
for (int[] p : pairs) {
int x = p[0], y = p[1];
g[x][y] = true;
g[y][x] = true;
v[x].add(y);
v[y].add(x);
}
List<Integer> nodes = new ArrayList<>();
for (int i = 0; i < 510; ++i) {
if (!v[i].isEmpty()) {
nodes.add(i);
g[i][i] = true;
}
}
nodes.sort(Comparator.comparingInt(a -> v[a].size()));
boolean equal = false;
int root = 0;
for (int i = 0; i < nodes.size(); ++i) {
int x = nodes.get(i);
int j = i + 1;
for (; j < nodes.size() && !g[x][nodes.get(j)]; ++j)
;
if (j < nodes.size()) {
int y = nodes.get(j);
if (v[x].size() == v[y].size()) {
equal = true;
}
for (int z : v[x]) {
if (!g[y][z]) {
return 0;
}
}
} else {
++root;
}
}
if (root > 1) {
return 0;
}
return equal ? 2 : 1;
}
}class Solution {
public:
int checkWays(vector<vector<int>>& pairs) {
vector<vector<bool>> g(510, vector<bool>(510));
vector<vector<int>> v(510);
for (auto& p : pairs) {
int x = p[0], y = p[1];
g[x][y] = g[y][x] = 1;
v[x].push_back(y);
v[y].push_back(x);
}
vector<int> nodes;
for (int i = 1; i <= 500; ++i) {
if (v[i].size()) {
nodes.push_back(i);
g[i][i] = 1;
}
}
sort(nodes.begin(), nodes.end(), [&](int x, int y) -> bool { return v[x].size() < v[y].size(); });
bool equal = 0;
int root = 0;
for (int i = 0; i < nodes.size(); ++i) {
int x = nodes[i];
int j = i + 1;
for (; j < nodes.size() && !g[x][nodes[j]]; ++j)
;
if (j < nodes.size()) {
int y = nodes[j];
if (v[x].size() == v[y].size()) equal = 1;
for (int z : v[x])
if (!g[y][z])
return 0;
} else
++root;
}
if (root > 1) return 0;
if (equal) return 2;
return 1;
}
};func checkWays(pairs [][]int) int {
g := make([][]bool, 510)
v := make([][]int, 510)
for i := range g {
g[i] = make([]bool, 510)
}
for _, p := range pairs {
x, y := p[0], p[1]
g[x][y] = true
g[y][x] = true
v[x] = append(v[x], y)
v[y] = append(v[y], x)
}
var nodes []int
for i := 1; i <= 500; i++ {
if len(v[i]) > 0 {
nodes = append(nodes, i)
g[i][i] = true
}
}
sort.Slice(nodes, func(i, j int) bool {
return len(v[nodes[i]]) < len(v[nodes[j]])
})
equal := false
root := 0
for i, x := range nodes {
j := i + 1
for ; j < len(nodes) && !g[x][nodes[j]]; j++ {
}
if j < len(nodes) {
y := nodes[j]
if len(v[x]) == len(v[y]) {
equal = true
}
for _, z := range v[x] {
if !g[y][z] {
return 0
}
}
} else {
root++
}
}
if root > 1 {
return 0
}
if equal {
return 2
}
return 1
}