README.md

1382. 将二叉搜索树变平衡

English Version

题目描述

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法，请你返回任意一种。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。

 

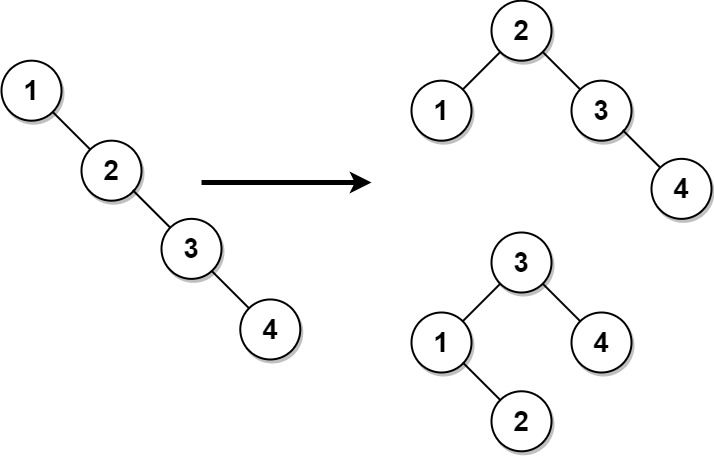
示例 1：

输入：root = [1,null,2,null,3,null,4,null,null]
输出：[2,1,3,null,null,null,4]
解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。

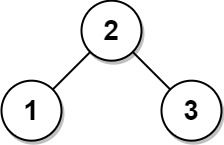
示例 2：

输入: root = [2,1,3]
输出: [2,1,3]

 

提示：

• 树节点的数目在 [1, 104] 范围内。
• 1 <= Node.val <= 105

解法

先中序遍历获取到升序排列的每个节点值，然后分治构建二叉树。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def balanceBST(self, root: TreeNode) -> TreeNode:
        def dfs(root):
            if root is None:
                return
            dfs(root.left)
            vals.append(root.val)
            dfs(root.right)

        def build(i, j):
            if i > j:
                return None
            mid = (i + j) >> 1
            root = TreeNode(vals[mid])
            root.left = build(i, mid - 1)
            root.right = build(mid + 1, j)
            return root

        vals = []
        dfs(root)
        return build(0, len(vals) - 1)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private List<Integer> vals;

    public TreeNode balanceBST(TreeNode root) {
        vals = new ArrayList<>();
        dfs(root);
        return build(0, vals.size() - 1);
    }

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        dfs(root.left);
        vals.add(root.val);
        dfs(root.right);
    }

    private TreeNode build(int i, int j) {
        if (i > j) {
            return null;
        }
        int mid = (i + j) >> 1;
        TreeNode root = new TreeNode(vals.get(mid));
        root.left = build(i, mid - 1);
        root.right = build(mid + 1, j);
        return root;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> vals;

    TreeNode* balanceBST(TreeNode* root) {
        dfs(root);
        return build(0, vals.size() - 1);
    }

    void dfs(TreeNode* root) {
        if (!root) return;
        dfs(root->left);
        vals.push_back(root->val);
        dfs(root->right);
    }

    TreeNode* build(int i, int j) {
        if (i > j) return nullptr;
        int mid = (i + j) >> 1;
        TreeNode* root = new TreeNode(vals[mid]);
        root->left = build(i, mid - 1);
        root->right = build(mid + 1, j);
        return root;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func balanceBST(root *TreeNode) *TreeNode {
	var vals []int
	var dfs func(root *TreeNode)
	dfs = func(root *TreeNode) {
		if root == nil {
			return
		}
		dfs(root.Left)
		vals = append(vals, root.Val)
		dfs(root.Right)
	}
	dfs(root)
	var build func(i, j int) *TreeNode
	build = func(i, j int) *TreeNode {
		if i > j {
			return nil
		}
		mid := (i + j) >> 1
		return &TreeNode{vals[mid], build(i, mid-1), build(mid+1, j)}
	}
	return build(0, len(vals)-1)
}

...