README_EN.md

1222. Queens That Can Attack the King

中文文档

Description

On an 8x8 chessboard, there can be multiple Black Queens and one White King.

Given an array of integer coordinates queens that represents the positions of the Black Queens, and a pair of coordinates king that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King.

 

Example 1:

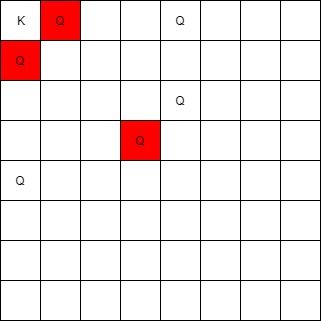
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]

Output: [[0,1],[1,0],[3,3]]

Explanation:  

The queen at [0,1] can attack the king cause they're in the same row. 

The queen at [1,0] can attack the king cause they're in the same column. 

The queen at [3,3] can attack the king cause they're in the same diagnal. 

The queen at [0,4] can't attack the king cause it's blocked by the queen at [0,1]. 

The queen at [4,0] can't attack the king cause it's blocked by the queen at [1,0]. 

The queen at [2,4] can't attack the king cause it's not in the same row/column/diagnal as the king.

Example 2:

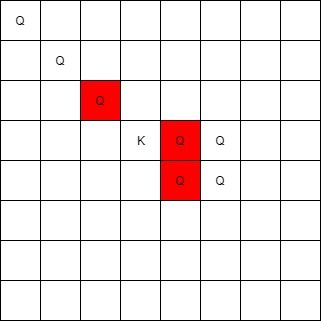
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]

Output: [[2,2],[3,4],[4,4]]

Example 3:

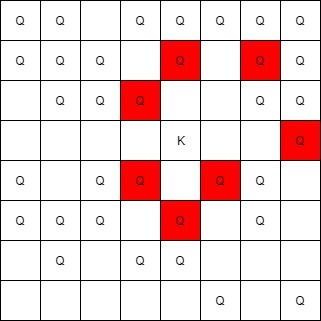
Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]

Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

 

Constraints:

• 1 <= queens.length <= 63
• queens[i].length == 2
• 0 <= queens[i][j] < 8
• king.length == 2
• 0 <= king[0], king[1] < 8
• At most one piece is allowed in a cell.

Solutions

Python3

class Solution:
    def queensAttacktheKing(
        self, queens: List[List[int]], king: List[int]
    ) -> List[List[int]]:
        n = 8
        s = {(i, j) for i, j in queens}
        ans = []
        for a, b in [
            [-1, 0],
            [1, 0],
            [0, -1],
            [0, 1],
            [1, 1],
            [1, -1],
            [-1, 1],
            [-1, -1],
        ]:
            x, y = king
            while 0 <= x + a < n and 0 <= y + b < n:
                x, y = x + a, y + b
                if (x, y) in s:
                    ans.append([x, y])
                    break
        return ans

Java

class Solution {
    private static final int N = 8;
    private int[][] dirs
        = new int[][] {{0, -1}, {0, 1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};

    public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) {
        Set<Integer> s = get(queens);
        List<List<Integer>> ans = new ArrayList<>();
        for (int[] dir : dirs) {
            int x = king[0], y = king[1];
            int a = dir[0], b = dir[1];
            while (x + a >= 0 && x + a < N && y + b >= 0 && y + b < N) {
                x += a;
                y += b;
                if (s.contains(x * N + y)) {
                    ans.add(Arrays.asList(x, y));
                    break;
                }
            }
        }
        return ans;
    }

    private Set<Integer> get(int[][] queens) {
        Set<Integer> ans = new HashSet<>();
        for (int[] queen : queens) {
            ans.add(queen[0] * N + queen[1]);
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
        unordered_set<int> s;
        int n = 8;
        for (auto& queen : queens) s.insert(queen[0] * n + queen[1]);
        vector<vector<int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
        vector<vector<int>> ans;
        for (auto& dir : dirs) {
            int x = king[0], y = king[1];
            int a = dir[0], b = dir[1];
            while (x + a >= 0 && x + a < n && y + b >= 0 && y + b < n) {
                x += a;
                y += b;
                if (s.count(x * n + y)) {
                    ans.push_back({x, y});
                    break;
                }
            }
        }
        return ans;
    }
};

Go

func queensAttacktheKing(queens [][]int, king []int) [][]int {
	s := make(map[int]bool)
	n := 8
	for _, queen := range queens {
		s[queen[0]*n+queen[1]] = true
	}
	dirs := [8][2]int{{0, -1}, {0, 1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}}
	var ans [][]int
	for _, dir := range dirs {
		x, y := king[0], king[1]
		a, b := dir[0], dir[1]
		for x+a >= 0 && x+a < n && y+b >= 0 && y+b < n {
			x, y = x+a, y+b
			if s[x*n+y] {
				ans = append(ans, []int{x, y})
				break
			}
		}
	}
	return ans
}

...