两位玩家分别扮演猫和老鼠,在一张 无向 图上进行游戏,两人轮流行动。
图的形式是:graph[a] 是一个列表,由满足 ab 是图中的一条边的所有节点 b 组成。
老鼠从节点 1 开始,第一个出发;猫从节点 2 开始,第二个出发。在节点 0 处有一个洞。
在每个玩家的行动中,他们 必须 沿着图中与所在当前位置连通的一条边移动。例如,如果老鼠在节点 1 ,那么它必须移动到 graph[1] 中的任一节点。
此外,猫无法移动到洞中(节点 0)。
然后,游戏在出现以下三种情形之一时结束:
- 如果猫和老鼠出现在同一个节点,猫获胜。
- 如果老鼠到达洞中,老鼠获胜。
- 如果某一位置重复出现(即,玩家的位置和移动顺序都与上一次行动相同),游戏平局。
给你一张图 graph ,并假设两位玩家都都以最佳状态参与游戏:
- 如果老鼠获胜,则返回
1; - 如果猫获胜,则返回
2; - 如果平局,则返回
0。
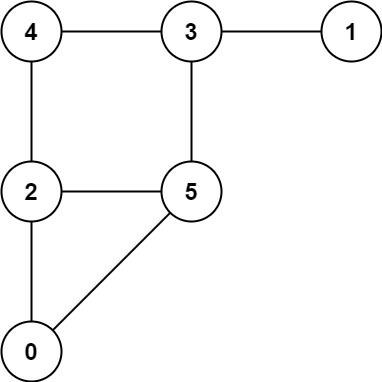
示例 1:
输入:graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] 输出:0
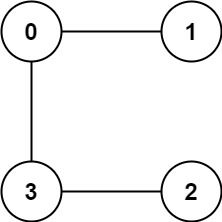
示例 2:
输入:graph = [[1,3],[0],[3],[0,2]] 输出:1
提示:
3 <= graph.length <= 501 <= graph[i].length < graph.length0 <= graph[i][j] < graph.lengthgraph[i][j] != igraph[i]互不相同- 猫和老鼠在游戏中总是移动
class Solution:
def catMouseGame(self, graph: List[List[int]]) -> int:
@cache
def dfs(i, j, k):
# 老鼠 / 猫 / 总步数
if k >= 2 * len(graph):
return 0 # 平局
if i == 0:
return 1 # 老鼠获胜
if i == j:
return 2 # 猫获胜
if k % 2: # 轮到猫行动
tie = False
for next in graph[j]:
if next == 0:
continue
x = dfs(i, next, k + 1)
if x == 2:
return 2
if x == 0:
# 继续寻找是否存在获胜的方案
tie = True
if tie:
return 0
return 1
else: # 轮到老鼠行动
tie = False
for next in graph[i]:
x = dfs(next, j, k + 1)
if x == 1:
return 1
if x == 0:
# 继续寻找是否存在获胜的方案
tie = True
if tie:
return 0
return 2
return dfs(1, 2, 0)class Solution {
private int[][][] memo;
private int[][] graph;
public int catMouseGame(int[][] graph) {
int n = graph.length;
this.graph = graph;
memo = new int[n][n][2 * n + 10];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < 2 * n + 10; ++k) {
memo[i][j][k] = -1;
}
}
}
return dfs(1, 2, 0);
}
private int dfs(int i, int j, int k) {
// 老鼠 / 猫 / 总步数
if (memo[i][j][k] != -1) {
return memo[i][j][k];
}
if (k >= 2 * graph.length) {
// 平局
memo[i][j][k] = 0;
} else if (i == 0) {
// 老鼠获胜
memo[i][j][k] = 1;
} else if (i == j) {
// 猫获胜
memo[i][j][k] = 2;
} else if (k % 2 == 1) {
// 轮到猫行动
boolean tie = false;
boolean win = false;
for (int next : graph[j]) {
if (next == 0) {
continue;
}
int x = dfs(i, next, k + 1);
if (x == 2) {
win = true;
memo[i][j][k] = 2;
break;
}
if (x == 0) {
// 继续寻找是否存在获胜的方案
tie = true;
}
}
if (!win) {
memo[i][j][k] = tie ? 0 : 1;
}
} else {
// 轮到老鼠行动
boolean tie = false;
boolean win = false;
for (int next : graph[i]) {
int x = dfs(next, j, k + 1);
if (x == 1) {
win = true;
memo[i][j][k] = 1;
break;
}
if (x == 0) {
// 继续寻找是否存在获胜的方案
tie = true;
}
}
if (!win) {
memo[i][j][k] = tie ? 0 : 2;
}
}
return memo[i][j][k];
}
}class Solution {
public:
vector<vector<vector<int>>> memo;
vector<vector<int>> graph;
int catMouseGame(vector<vector<int>>& graph) {
int n = graph.size();
this->graph = graph;
memo.resize(n, vector<vector<int>>(n, vector<int>(2 * n + 10, -1)));
return dfs(1, 2, 0);
}
int dfs(int i, int j, int k) {
if (memo[i][j][k] != -1) return memo[i][j][k];
if (k >= 2 * graph.size())
memo[i][j][k] = 0;
else if (i == 0)
memo[i][j][k] = 1;
else if (i == j)
memo[i][j][k] = 2;
else if (k % 2) {
bool tie = false, win = false;
for (int next : graph[j]) {
if (next == 0) continue;
int x = dfs(i, next, k + 1);
if (x == 2) {
win = true;
memo[i][j][k] = 2;
break;
}
if (x == 0) tie = true;
}
if (!win) memo[i][j][k] = tie ? 0 : 1;
} else {
bool tie = false, win = false;
for (int next : graph[i]) {
int x = dfs(next, j, k + 1);
if (x == 1) {
win = true;
memo[i][j][k] = 1;
break;
}
if (x == 0) tie = true;
}
if (!win) memo[i][j][k] = tie ? 0 : 2;
}
return memo[i][j][k];
}
};func catMouseGame(graph [][]int) int {
n := len(graph)
memo := make([][][]int, n)
for i := range memo {
memo[i] = make([][]int, n)
for j := range memo[i] {
memo[i][j] = make([]int, 2*n+10)
for k := range memo[i][j] {
memo[i][j][k] = -1
}
}
}
var dfs func(i, j, k int) int
dfs = func(i, j, k int) int {
if memo[i][j][k] != -1 {
return memo[i][j][k]
}
if k >= 2*len(graph) {
memo[i][j][k] = 0
} else if i == 0 {
memo[i][j][k] = 1
} else if i == j {
memo[i][j][k] = 2
} else if k%2 == 1 {
tie, win := false, false
for _, next := range graph[j] {
if next == 0 {
continue
}
x := dfs(i, next, k+1)
if x == 2 {
win = true
memo[i][j][k] = 2
break
}
if x == 0 {
tie = true
}
}
if !win {
if tie {
memo[i][j][k] = 0
} else {
memo[i][j][k] = 1
}
}
} else {
tie, win := false, false
for _, next := range graph[i] {
x := dfs(next, j, k+1)
if x == 1 {
win = true
memo[i][j][k] = 1
break
}
if x == 0 {
tie = true
}
}
if !win {
if tie {
memo[i][j][k] = 0
} else {
memo[i][j][k] = 2
}
}
}
return memo[i][j][k]
}
return dfs(1, 2, 0)
}