有一个 m × n 的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。
这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。
岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
返回网格坐标 result 的 2D 列表 ,其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。
示例 1:
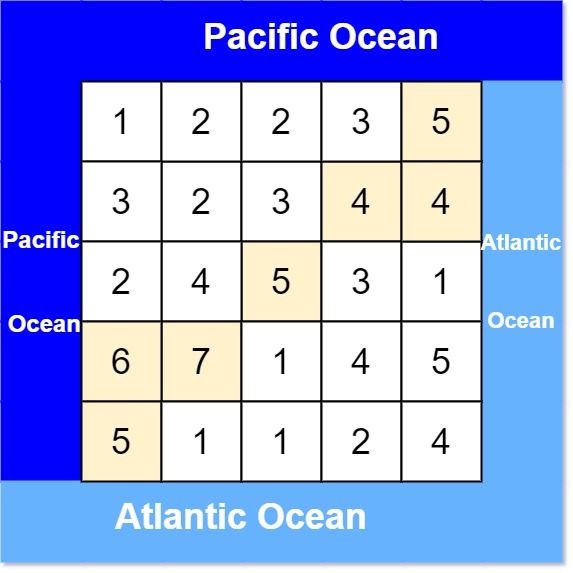
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]] 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
示例 2:
输入: heights = [[2,1],[1,2]] 输出: [[0,0],[0,1],[1,0],[1,1]]
提示:
m == heights.lengthn == heights[r].length1 <= m, n <= 2000 <= heights[r][c] <= 105
反向寻找,从海洋开始逆流,只要比该陆地高的地方就能逆流。最后是寻找两个海洋的水流都能经过的陆地即为结果。
class Solution:
def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
def bfs(q, vis):
while q:
for _ in range(len(q)):
i, j = q.popleft()
for a, b in [[0, -1], [0, 1], [1, 0], [-1, 0]]:
x, y = i + a, j + b
if (
0 <= x < m
and 0 <= y < n
and (x, y) not in vis
and heights[x][y] >= heights[i][j]
):
vis.add((x, y))
q.append((x, y))
m, n = len(heights), len(heights[0])
vis1, vis2 = set(), set()
q1 = deque()
q2 = deque()
for i in range(m):
for j in range(n):
if i == 0 or j == 0:
vis1.add((i, j))
q1.append((i, j))
if i == m - 1 or j == n - 1:
vis2.add((i, j))
q2.append((i, j))
bfs(q1, vis1)
bfs(q2, vis2)
return [
(i, j)
for i in range(m)
for j in range(n)
if (i, j) in vis1 and (i, j) in vis2
]class Solution {
private int[][] heights;
private int m;
private int n;
public List<List<Integer>> pacificAtlantic(int[][] heights) {
m = heights.length;
n = heights[0].length;
this.heights = heights;
Deque<int[]> q1 = new LinkedList<>();
Deque<int[]> q2 = new LinkedList<>();
Set<Integer> vis1 = new HashSet<>();
Set<Integer> vis2 = new HashSet<>();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || j == 0) {
vis1.add(i * n + j);
q1.offer(new int[] {i, j});
}
if (i == m - 1 || j == n - 1) {
vis2.add(i * n + j);
q2.offer(new int[] {i, j});
}
}
}
bfs(q1, vis1);
bfs(q2, vis2);
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int x = i * n + j;
if (vis1.contains(x) && vis2.contains(x)) {
ans.add(Arrays.asList(i, j));
}
}
}
return ans;
}
private void bfs(Deque<int[]> q, Set<Integer> vis) {
int[] dirs = {-1, 0, 1, 0, -1};
while (!q.isEmpty()) {
for (int k = q.size(); k > 0; --k) {
int[] p = q.poll();
for (int i = 0; i < 4; ++i) {
int x = p[0] + dirs[i];
int y = p[1] + dirs[i + 1];
if (x >= 0 && x < m && y >= 0 && y < n && !vis.contains(x * n + y)
&& heights[x][y] >= heights[p[0]][p[1]]) {
vis.add(x * n + y);
q.offer(new int[] {x, y});
}
}
}
}
}
}typedef pair<int, int> pii;
class Solution {
public:
vector<vector<int>> heights;
int m;
int n;
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
m = heights.size();
n = heights[0].size();
this->heights = heights;
queue<pii> q1;
queue<pii> q2;
unordered_set<int> vis1;
unordered_set<int> vis2;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || j == 0) {
vis1.insert(i * n + j);
q1.emplace(i, j);
}
if (i == m - 1 || j == n - 1) {
vis2.insert(i * n + j);
q2.emplace(i, j);
}
}
}
bfs(q1, vis1);
bfs(q2, vis2);
vector<vector<int>> ans;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int x = i * n + j;
if (vis1.count(x) && vis2.count(x)) {
ans.push_back({i, j});
}
}
}
return ans;
}
void bfs(queue<pii>& q, unordered_set<int>& vis) {
vector<int> dirs = {-1, 0, 1, 0, -1};
while (!q.empty()) {
for (int k = q.size(); k > 0; --k) {
auto p = q.front();
q.pop();
for (int i = 0; i < 4; ++i) {
int x = p.first + dirs[i];
int y = p.second + dirs[i + 1];
if (x >= 0 && x < m && y >= 0 && y < n && !vis.count(x * n + y) && heights[x][y] >= heights[p.first][p.second]) {
vis.insert(x * n + y);
q.emplace(x, y);
}
}
}
}
}
};func pacificAtlantic(heights [][]int) [][]int {
m, n := len(heights), len(heights[0])
vis1 := make(map[int]bool)
vis2 := make(map[int]bool)
var q1 [][]int
var q2 [][]int
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if i == 0 || j == 0 {
vis1[i*n+j] = true
q1 = append(q1, []int{i, j})
}
if i == m-1 || j == n-1 {
vis2[i*n+j] = true
q2 = append(q2, []int{i, j})
}
}
}
dirs := []int{-1, 0, 1, 0, -1}
bfs := func(q [][]int, vis map[int]bool) {
for len(q) > 0 {
for k := len(q); k > 0; k-- {
p := q[0]
q = q[1:]
for i := 0; i < 4; i++ {
x, y := p[0]+dirs[i], p[1]+dirs[i+1]
if x >= 0 && x < m && y >= 0 && y < n && !vis[x*n+y] && heights[x][y] >= heights[p[0]][p[1]] {
vis[x*n+y] = true
q = append(q, []int{x, y})
}
}
}
}
}
bfs(q1, vis1)
bfs(q2, vis2)
var ans [][]int
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
x := i*n + j
if vis1[x] && vis2[x] {
ans = append(ans, []int{i, j})
}
}
}
return ans
}function pacificAtlantic(heights: number[][]): number[][] {
const m = heights.length;
const n = heights[0].length;
const dirs = [
[1, 0],
[0, 1],
[-1, 0],
[0, -1],
];
const gird = new Array(m).fill(0).map(() => new Array(n).fill(0));
const isVis = new Array(m).fill(0).map(() => new Array(n).fill(false));
const dfs = (i: number, j: number) => {
if (isVis[i][j]) {
return;
}
gird[i][j]++;
isVis[i][j] = true;
const h = heights[i][j];
for (const [x, y] of dirs) {
if (h <= (heights[i + x] ?? [])[j + y]) {
dfs(i + x, j + y);
}
}
};
for (let i = 0; i < n; i++) {
dfs(0, i);
}
for (let i = 0; i < m; i++) {
dfs(i, 0);
}
isVis.forEach(v => v.fill(false));
for (let i = 0; i < n; i++) {
dfs(m - 1, i);
}
for (let i = 0; i < m; i++) {
dfs(i, n - 1);
}
const res = [];
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (gird[i][j] === 2) {
res.push([i, j]);
}
}
}
return res;
}