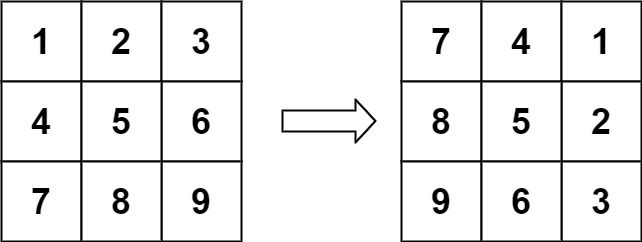
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
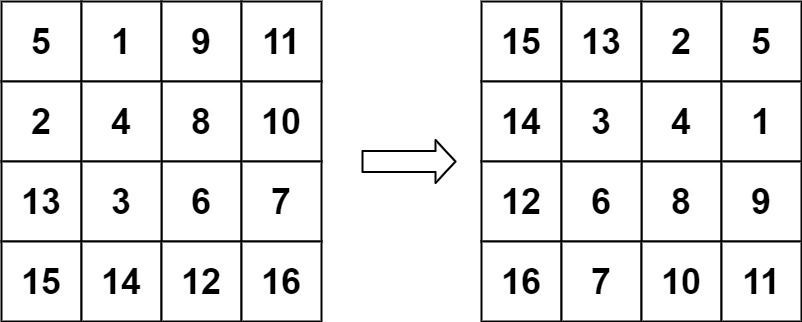
示例 2:
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
s, n = 0, len(matrix)
while s < (n >> 1):
e = n - s - 1
for i in range(s, e):
t = matrix[i][e]
matrix[i][e] = matrix[s][i]
matrix[s][i] = matrix[n - i - 1][s]
matrix[n - i - 1][s] = matrix[e][n - i - 1]
matrix[e][n - i - 1] = t
s += 1class Solution {
public void rotate(int[][] matrix) {
int s = 0, n = matrix.length;
while (s < (n >> 1)) {
int e = n - s - 1;
for (int i = s; i < e; ++i) {
int t = matrix[i][e];
matrix[i][e] = matrix[s][i];
matrix[s][i] = matrix[n - i - 1][s];
matrix[n - i - 1][s] = matrix[e][n - i - 1];
matrix[e][n - i - 1] = t;
}
++s;
}
}
}class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
if (n <= 1) return;
// 先做转置
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
swap(matrix[i][j], matrix[j][i]);
}
}
// 再做水平互换
for (int i = 0; i < n; i++) {
for (int j = 0; j < n / 2; j++) {
swap(matrix[i][j], matrix[i][n - 1 - j]);
}
}
}
};/**
* @param {number[][]} matrix
* @return {void} Do not return anything, modify matrix in-place instead.
*/
var rotate = function (matrix) {
const n = matrix.length;
for (let i = 0; i < n; i++) {
for (let j = 0; j <= i; j++) {
[matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
}
}
for (let i = 0, j = n - 1; i < j; i++, j--) {
for (let k = 0; k < n; k++) {
[matrix[k][i], matrix[k][j]] = [matrix[k][j], matrix[k][i]];
}
}
};/**
* @param {number[][]} matrix
* @return {void} Do not return anything, modify matrix in-place instead.
*/
var rotate = function (matrix) {
matrix.reverse();
for (let i = 0; i < matrix.length; i++) {
for (let j = 0; j < i; j++) {
[matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
}
}
};/**
Do not return anything, modify matrix in-place instead.
*/
function rotate(matrix: number[][]): void {
let n = matrix[0].length;
for (let i = 0; i < Math.floor(n / 2); i++) {
for (let j = 0; j < Math.floor((n + 1) / 2); j++) {
let tmp = matrix[i][j];
matrix[i][j] = matrix[n - 1 - j][i];
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
matrix[j][n - 1 - i] = tmp;
}
}
}impl Solution {
pub fn rotate(matrix: &mut Vec<Vec<i32>>) {
let n = matrix.len();
for i in 0..n / 2 {
for j in i..n - i - 1 {
let t = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][i];
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
matrix[j][n - i - 1] = t;
}
}
}
}func rotate(matrix [][]int) {
n := len(matrix)
for i := 0; i < n; i++ {
for j := i; j < n; j++ {
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
}
}
for i := 0; i < n; i++ {
for j, k := 0, n-1; j < k; j, k = j+1, k-1 {
matrix[i][j], matrix[i][k] = matrix[i][k], matrix[i][j]
}
}
}