剑指 Offer II 054. 所有大于等于节点的值之和

题目描述

给定一个二叉搜索树，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

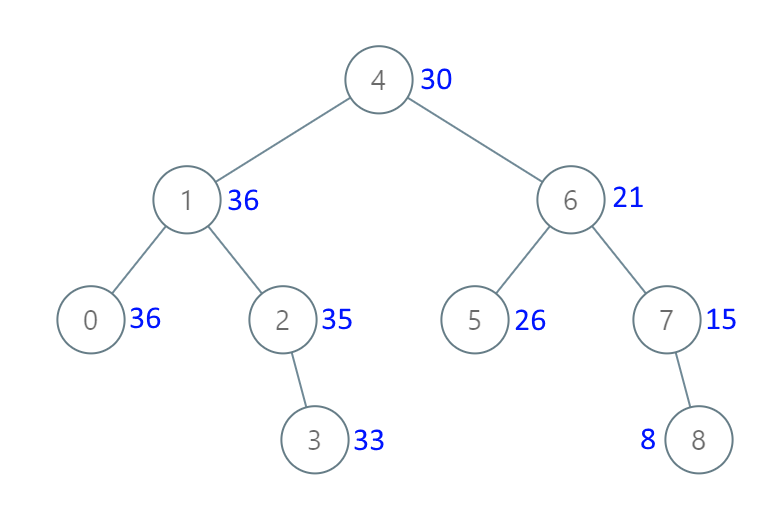
示例 1：

输入：root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 10⁴之间。
每个节点的值介于 -10⁴ 和 10⁴ 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。

注意：

本题与主站 538 题相同： https://leetcode.cn/problems/convert-bst-to-greater-tree/
本题与主站 1038 题相同：https://leetcode.cn/problems/binary-search-tree-to-greater-sum-tree/

解法

前言

二叉搜索树的中序遍历（左根右）结果是一个单调递增的有序序列，我们反序进行中序遍历（右根左），即可以得到一个单调递减的有序序列。通过累加单调递减的有序序列，我们可以得到大于等于 node.val 的新值，并重新赋值给 node。

关于反序中序遍历，有三种方法，一是递归遍历，二是栈实现非递归遍历，三是 Morris 遍历。

方法一：递归

按照“右根左”的顺序，递归遍历二叉搜索树，累加遍历到的所有节点值到 $s$ 中，然后每次赋值给对应的 node 节点。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉搜索树的节点数。

方法二：Morris 遍历

Morris 遍历无需使用栈，时间复杂度 $O(n)$，空间复杂度为 $O(1)$。核心思想是：

定义 s 表示二叉搜索树节点值累加和。遍历二叉树节点：

若当前节点 root 的右子树为空，将当前节点值添加至 s 中，更新当前节点值为 s，并将当前节点更新为 root.left。
若当前节点 root 的右子树不为空，找到右子树的最左节点 next（也即是 root 节点在中序遍历下的后继节点）：
- 若后继节点 next 的左子树为空，将后继节点的左子树指向当前节点 root，并将当前节点更新为 root.right。
- 若后继节点 next 的左子树不为空，将当前节点值添加 s 中，更新当前节点值为 s，然后将后继节点左子树指向空（即解除 next 与 root 的指向关系），并将当前节点更新为 root.left。
循环以上步骤，直至二叉树节点为空，遍历结束。
最后返回二叉搜索树根节点即可。

Morris 反序中序遍历跟 Morris 中序遍历思路一致，只是将中序遍历的“左根右”变为“右根左”。

Python3

递归遍历：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def convertBST(self, root: TreeNode) -> TreeNode:
        def dfs(root):
            nonlocal s
            if root is None:
                return
            dfs(root.right)
            s += root.val
            root.val = s
            dfs(root.left)

        s = 0
        dfs(root)
        return root

Morris 遍历：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def convertBST(self, root: TreeNode) -> TreeNode:
        s = 0
        node = root
        while root:
            if root.right is None:
                s += root.val
                root.val = s
                root = root.left
            else:
                next = root.right
                while next.left and next.left != root:
                    next = next.left
                if next.left is None:
                    next.left = root
                    root = root.right
                else:
                    s += root.val
                    root.val = s
                    next.left = None
                    root = root.left
        return node

Java

递归遍历：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int s;

    public TreeNode convertBST(TreeNode root) {
        dfs(root);
        return root;
    }

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        dfs(root.right);
        s += root.val;
        root.val = s;
        dfs(root.left);
    }
}

Morris 遍历：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode convertBST(TreeNode root) {
        int s = 0;
        TreeNode node = root;
        while (root != null) {
            if (root.right == null) {
                s += root.val;
                root.val = s;
                root = root.left;
            } else {
                TreeNode next = root.right;
                while (next.left != null && next.left != root) {
                    next = next.left;
                }
                if (next.left == null) {
                    next.left = root;
                    root = root.right;
                } else {
                    s += root.val;
                    root.val = s;
                    next.left = null;
                    root = root.left;
                }
            }
        }
        return node;
    }
}

C++

递归遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int s = 0;

    TreeNode* convertBST(TreeNode* root) {
        dfs(root);
        return root;
    }

    void dfs(TreeNode* root) {
        if (!root) return;
        dfs(root->right);
        s += root->val;
        root->val = s;
        dfs(root->left);
    }
};

Morris 遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        int s = 0;
        TreeNode* node = root;
        while (root) {
            if (root->right == nullptr) {
                s += root->val;
                root->val = s;
                root = root->left;
            } else {
                TreeNode* next = root->right;
                while (next->left && next->left != root) {
                    next = next->left;
                }
                if (next->left == nullptr) {
                    next->left = root;
                    root = root->right;
                } else {
                    s += root->val;
                    root->val = s;
                    next->left = nullptr;
                    root = root->left;
                }
            }
        }
        return node;
    }
};

Go

递归遍历：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func convertBST(root *TreeNode) *TreeNode {
	s := 0
	var dfs func(*TreeNode)
	dfs = func(root *TreeNode) {
		if root == nil {
			return
		}
		dfs(root.Right)
		s += root.Val
		root.Val = s
		dfs(root.Left)
	}
	dfs(root)
	return root
}

Morris 遍历：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func convertBST(root *TreeNode) *TreeNode {
	s := 0
	node := root
	for root != nil {
		if root.Right == nil {
			s += root.Val
			root.Val = s
			root = root.Left
		} else {
			next := root.Right
			for next.Left != nil && next.Left != root {
				next = next.Left
			}
			if next.Left == nil {
				next.Left = root
				root = root.Right
			} else {
				s += root.Val
				root.Val = s
				next.Left = nil
				root = root.Left
			}
		}
	}
	return node
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var convertBST = function (root) {
    let s = 0;
    function dfs(root) {
        if (!root) {
            return;
        }
        dfs(root.right);
        s += root.val;
        root.val = s;
        dfs(root.left);
    }
    dfs(root);
    return root;
};

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

剑指 Offer II 054. 所有大于等于节点的值之和

题目描述

解法

Python3

Java

C++

Go

JavaScript

...

Files

README.md

Latest commit

History

README.md

File metadata and controls

剑指 Offer II 054. 所有大于等于节点的值之和

题目描述

解法

Python3

Java

C++

Go

JavaScript

...