README.md

剑指 Offer II 040. 矩阵中最大的矩形

题目描述

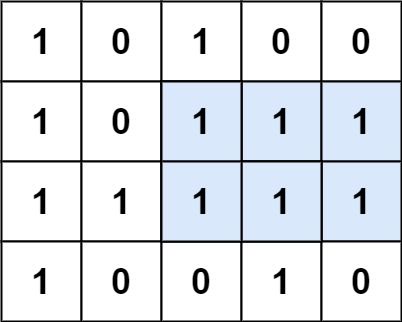
给定一个由 0 和 1 组成的矩阵 matrix ，找出只包含 1 的最大矩形，并返回其面积。

注意：此题 matrix 输入格式为一维 01 字符串数组。

 

示例 1：

输入：matrix = ["10100","10111","11111","10010"]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = []
输出：0

示例 3：

输入：matrix = ["0"]
输出：0

示例 4：

输入：matrix = ["1"]
输出：1

示例 5：

输入：matrix = ["00"]
输出：0

 

提示：

• rows == matrix.length
• cols == matrix[0].length
• 0 <= row, cols <= 200
• matrix[i][j] 为 '0' 或 '1'

 

注意：本题与主站 85 题相同（输入参数格式不同）： https://leetcode.cn/problems/maximal-rectangle/

解法

方法一：单调栈

把每一行视为柱状图的底部，对每一行求柱状图的最大面积即可。

时间复杂度 $O(mn)$，其中 $m$ 表示 $matrix$ 的行数，$n$ 表示 $matrix$ 的列数。

Python3

class Solution:
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        if not matrix:
            return 0
        heights = [0] * len(matrix[0])
        ans = 0
        for row in matrix:
            for j, v in enumerate(row):
                if v == "1":
                    heights[j] += 1
                else:
                    heights[j] = 0
            ans = max(ans, self.largestRectangleArea(heights))
        return ans

    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        stk = []
        left = [-1] * n
        right = [n] * n
        for i, h in enumerate(heights):
            while stk and heights[stk[-1]] >= h:
                stk.pop()
            if stk:
                left[i] = stk[-1]
            stk.append(i)
        stk = []
        for i in range(n - 1, -1, -1):
            h = heights[i]
            while stk and heights[stk[-1]] >= h:
                stk.pop()
            if stk:
                right[i] = stk[-1]
            stk.append(i)
        return max(h * (right[i] - left[i] - 1) for i, h in enumerate(heights))

Java

class Solution {
    public int maximalRectangle(String[] matrix) {
        if (matrix == null || matrix.length == 0) {
            return 0;
        }
        int n = matrix[0].length();
        int[] heights = new int[n];
        int ans = 0;
        for (var row : matrix) {
            for (int j = 0; j < n; ++j) {
                if (row.charAt(j) == '1') {
                    heights[j] += 1;
                } else {
                    heights[j] = 0;
                }
            }
            ans = Math.max(ans, largestRectangleArea(heights));
        }
        return ans;
    }

    private int largestRectangleArea(int[] heights) {
        int res = 0, n = heights.length;
        Deque<Integer> stk = new ArrayDeque<>();
        int[] left = new int[n];
        int[] right = new int[n];
        Arrays.fill(right, n);
        for (int i = 0; i < n; ++i) {
            while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) {
                right[stk.pop()] = i;
            }
            left[i] = stk.isEmpty() ? -1 : stk.peek();
            stk.push(i);
        }
        for (int i = 0; i < n; ++i) {
            res = Math.max(res, heights[i] * (right[i] - left[i] - 1));
        }
        return res;
    }
}

C++

• 首先在柱状图中求最大矩形面积可以通过单调栈，维护每一列的左边第一个比它小的位置 $L$，和右边第一个比它小的位置 $R$，就能得到以这一列为高的最大矩形面积为 $(R-L-1)*h$。
• 考虑每一行作为底边的柱状图中，能够得到的最大的矩形面积。再对每一行的最大面积取 $max$ 就是最终的答案。
• 柱状图中每一列的高可以通过类似前缀和的方式去维护。
• 假设矩阵大小为 $n*m$，那么时间复杂为 $O(nm)$，空间复杂度为 $O(m)$。

class Solution {
public:
    int h[210];
    int l[210], r[210];
    int maximalRectangle(vector<string>& matrix) {
        int n = matrix.size();
        if (n == 0) return 0;
        int m = matrix[0].size();
        int ans = 0;
        stack<int> st;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                h[j] = (matrix[i][j] == '1' ? h[j] + 1 : 0);
                while (st.size() && h[j] <= h[st.top()]) {
                    ans = max(ans, (j - l[st.top()] - 1) * h[st.top()]);
                    st.pop();
                }
                if (st.size())
                    l[j] = st.top();
                else
                    l[j] = -1;
                st.push(j);
            }
            while (st.size()) {
                ans = max(ans, (m - 1 - l[st.top()]) * h[st.top()]);
                st.pop();
            }
        }
        return ans;
    }
};

class Solution {
public:
    int maximalRectangle(vector<string>& matrix) {
        if (matrix.empty()) return 0;
        int n = matrix[0].size();
        vector<int> heights(n);
        int ans = 0;
        for (auto& row : matrix) {
            for (int j = 0; j < n; ++j) {
                if (row[j] == '1') ++heights[j];
                else heights[j] = 0;
            }
            ans = max(ans, largestRectangleArea(heights));
        }
        return ans;
    }

    int largestRectangleArea(vector<int>& heights) {
        int res = 0, n = heights.size();
        stack<int> stk;
        vector<int> left(n, -1);
        vector<int> right(n, n);
        for (int i = 0; i < n; ++i) {
            while (!stk.empty() && heights[stk.top()] >= heights[i]) {
                right[stk.top()] = i;
                stk.pop();
            }
            if (!stk.empty()) left[i] = stk.top();
            stk.push(i);
        }
        for (int i = 0; i < n; ++i)
            res = max(res, heights[i] * (right[i] - left[i] - 1));
        return res;
    }
};

Go

func maximalRectangle(matrix []string) int {
	if len(matrix) == 0 {
		return 0
	}
	n := len(matrix[0])
	heights := make([]int, n)
	ans := 0
	for _, row := range matrix {
		for j, v := range row {
			if v == '1' {
				heights[j]++
			} else {
				heights[j] = 0
			}
		}
		ans = max(ans, largestRectangleArea(heights))
	}
	return ans
}

func largestRectangleArea(heights []int) int {
	res, n := 0, len(heights)
	var stk []int
	left, right := make([]int, n), make([]int, n)
	for i := range right {
		right[i] = n
	}
	for i, h := range heights {
		for len(stk) > 0 && heights[stk[len(stk)-1]] >= h {
			right[stk[len(stk)-1]] = i
			stk = stk[:len(stk)-1]
		}
		if len(stk) > 0 {
			left[i] = stk[len(stk)-1]
		} else {
			left[i] = -1
		}
		stk = append(stk, i)
	}
	for i, h := range heights {
		res = max(res, h*(right[i]-left[i]-1))
	}
	return res
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

...