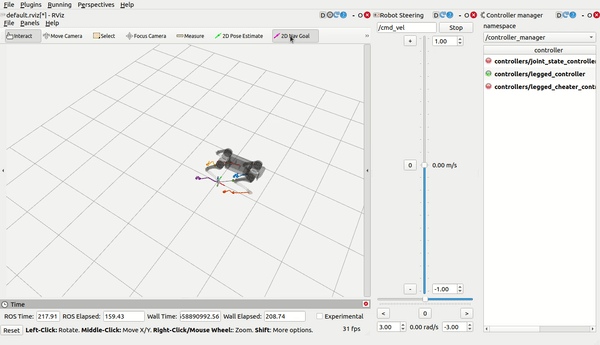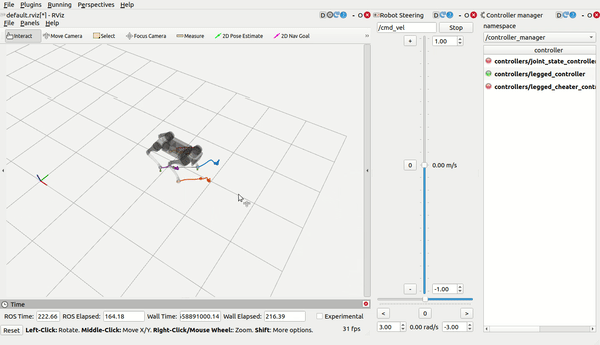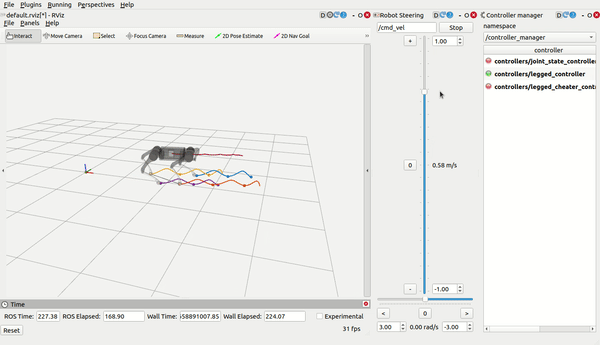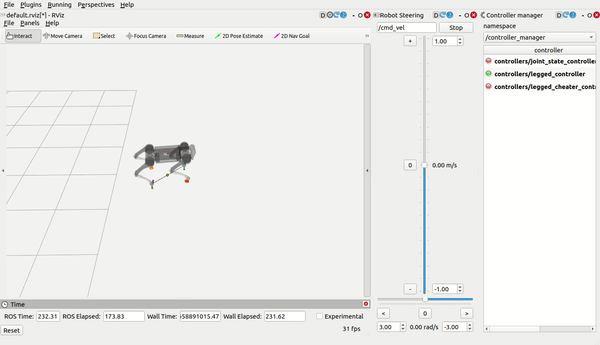
legged_control is an NMPC-WBC legged robot control stack and framework based on OCS2 and ros-control.
The advantage shows below:
- To the author's best knowledge, this framework is probably the best-performing open-source legged robot MPC control framework;
- You can deploy this framework in your A1 robot within a few hours;
- Thanks to the ros-control interface, you can easily use this framework for your custom robot.
I believe this framework can provide a high-performance and easy-to-use model-based baseline for the legged robot community.
test.mp4
The source code is hosted on GitHub: qiayuanliao/legged_control.
# Clone legged_control
git clone [email protected]:qiayuanliao/legged_control.git
OCS2 is a huge monorepo; DO NOT try to compile the whole repo. You only need to compile ocs2_legged_robot_ros and its dependencies following the step below.
- You are supposed to clone the OCS2, pinocchio, and hpp-fcl as described in the documentation of OCS2.
# Clone OCS2 git clone [email protected]:leggedrobotics/ocs2.git # Clone pinocchio git clone --recurse-submodules https://github.com/leggedrobotics/pinocchio.git # Clone hpp-fcl git clone --recurse-submodules https://github.com/leggedrobotics/hpp-fcl.git # Clone ocs2_robotic_assets git clone https://github.com/leggedrobotics/ocs2_robotic_assets.git # Install dependencies sudo apt install liburdfdom-dev liboctomap-dev libassimp-dev - Compile the
ocs2_legged_robot_rospackage with catkin tools instead ofcatkin_make. It will take you about ten minutes.Ensure you can command the ANYmal as shown in the document and below.catkin config -DCMAKE_BUILD_TYPE=RelWithDebInfo catkin build ocs2_legged_robot_ros
Build the source code of legged_control by:
catkin build legged_controllers unitree_description
Build the simulation (DO NOT run on the onboard computer)
catkin build legged_gazebo
Build the hardware interface real robot. If you use your computer only for simulation, you DO NOT need to compile unitree_hw (TODO: add a legged prefix to the package name)
catkin build unitree_hw
- Set your robot type as an environment variable: ROBOT_TYPE
export ROBOT_TYPE=a1
- Run the simulation:
roslaunch unitree_description empty_world.launch
Or on the robot hardware:
roslaunch unitree_hw unitree_hw.launch
- Load the controller:
roslaunch legged_controllers load_controller.launch cheater:=false
- Start the
legged_controllerorlegged_cheater_controller, NOTE that you are not allowed to start thelegged_cheater_controllerin real hardware!
rosservice call /controller_manager/switch_controller "start_controllers: ['controllers/legged_controller']
stop_controllers: ['']
strictness: 0
start_asap: false
timeout: 0.0"
Or, you can start the controller using rqt_controller_manager GUI:
sudo apt install ros-noetic-rqt-controller-manager
rosrun rqt_controller_manager rqt_controller_manager
- Set the gait in the terminal of
load_controller.launch, then use RViz (you need to add what you want to display by yourself) and control the robot bycmd_velandmove_base_simple/goal:
- THE GAIT AND THE GOAL ARE COMPLETELY DIFFERENT AND SEPARATED! You don't need to type stance while the robot is lying on the ground with four foot touching the ground; it's completely wrong since the robot is already in the stance gait.
- The target_trajectories_publisher is for demonstration. You can combine the trajectory publisher and gait command into a very simple node to add gamepad and keyboard input for different gaits and torso heights and to start/stop controller (by ros service).
The system framework diagram is shown below.
- The robot torso's desired velocity or position goal is converted to state trajectory and then sent to the NMPC;
- The NMPC will evaluate an optimized system state and input.
- The Whole-body Controller (WBC) figures out the joint torques according to the optimized states and inputs from the NMPC.
- The torque is set as a feed-forward term and is sent to the robot's motor controller. Low-gain joint-space position and velocity PD commands are sent to the robot's motors to reduce the shock during foot contact and for better tracking performance.
- The NMPC and WBC need to know the current robot state, the base orientation, and the joint state, all obtained directly from the IMU and the motors. Running in the same loop with WBC, a linear Kalman filter[1] estimates the base position and velocity from base orientation, base acceleration, and joint foot position measurements.
The main module of the entire control framework is NMPC and WBC, and the following is only a very brief introduction.
The NMPC part solves the following optimization problems at each cycle through the formulation and solving interfaces provided by OCS2:
For this framework, we defined system state
where
- Friction cone;
- No motion at the standing foot;
- The z-axis position of the swinging foot satisfies the gait-generated curve.
To solve this optimal control problem, a multiple shooting is formulated to transcribe the optimal control problem to a nonlinear program (NLP) problem, and the NLP problem is solved using Sequential Quadratic Programming (SQP). The QP subproblem is solved using HPIPM. For more details [2, 3]
WBC only considers the current moment. Several tasks are defined in the table above. Each task is the equality constraints or inequality constraints on decision variables. The decision variables of WBC are:
where
People with ROS foundation should be able to run through simulation and real machine deployment within a few hours. The following shows some known laboratories that have run through this framework on their own A1 objects. and the time spent The table below shows the labs successfully deploying this repo in their real A1; feel free to open a PR to update it. (because the code they got at the time was not stable, so the spend time cannot represent the their level).
| Lab | XPeng Robotics | Unitree | Hybrid Robotics |
|---|---|---|---|
| Spend Time | 1 day | - | 2 hours |
I recommended to use an external computing device such as NUC to run this control framework. The author uses the 11th generation of NUC, and the computing frequency of NMPC can be close to 200Hz.
Deploying this framework to your robot is very simple, the steps are as follows:
- Imitate the
UnitreeHWclass in legged_examples/legged_unitree/unitree_hw , inheritLeggedHWand implement theread()andwrite()functions of the hardware interface; - Imitate the legged_examples/legged_unitree/unitree_description, write the xarco of the robot and generate the URDF file, note that the names of the joint and link need to be the same as unitree_description.
[1] T. Flayols, A. Del Prete, P. Wensing, A. Mifsud, M. Benallegue, and O. Stasse, “Experimental evaluation of simple estimators for humanoid robots,” IEEE-RAS Int. Conf. Humanoid Robot., pp. 889–895, 2017, doi: 10.1109/HUMANOIDS.2017.8246977.
[2] J. P. Sleiman, F. Farshidian, M. V. Minniti, and M. Hutter, “A Unified MPC Framework for Whole-Body Dynamic Locomotion and Manipulation,” IEEE Robot. Autom. Lett., vol. 6, no. 3, pp. 4688–4695, 2021, doi: 10.1109/LRA.2021.3068908.
[3] R. Grandia, F. Jenelten, S. Yang, F. Farshidian, and M. Hutter, “Perceptive Locomotion through Nonlinear Model Predictive Control,” (submitted to) IEEE Trans. Robot., no. August, 2022, doi: 10.48550/arXiv.2208.08373.
[4] C. Dario Bellicoso, C. Gehring, J. Hwangbo, P. Fankhauser, and M. Hutter, “Perception-less terrain adaptation through whole body control and hierarchical optimization,” in IEEE-RAS International Conference on Humanoid Robots, 2016, pp. 558–564, doi: 10.1109/HUMANOIDS.2016.7803330.