
Workshop Instructions
+ +In order to understand the workflow and initial parameter sets +provided with this tutorial, we must first briefly describe prior +studies that led to the creation of the data you will aim to simulate. +This tutorial is based on results from Jones et al. 2009 where, using +MEG, we recorded spontaneous (pre-stimulus) alpha (7-14 Hz) and beta +(15-20 Hz) rhythms that arise as part of the mu-complex from the primary +somatosensory cortex (S1) [1]. (Figure 1. See also [2-4].)
+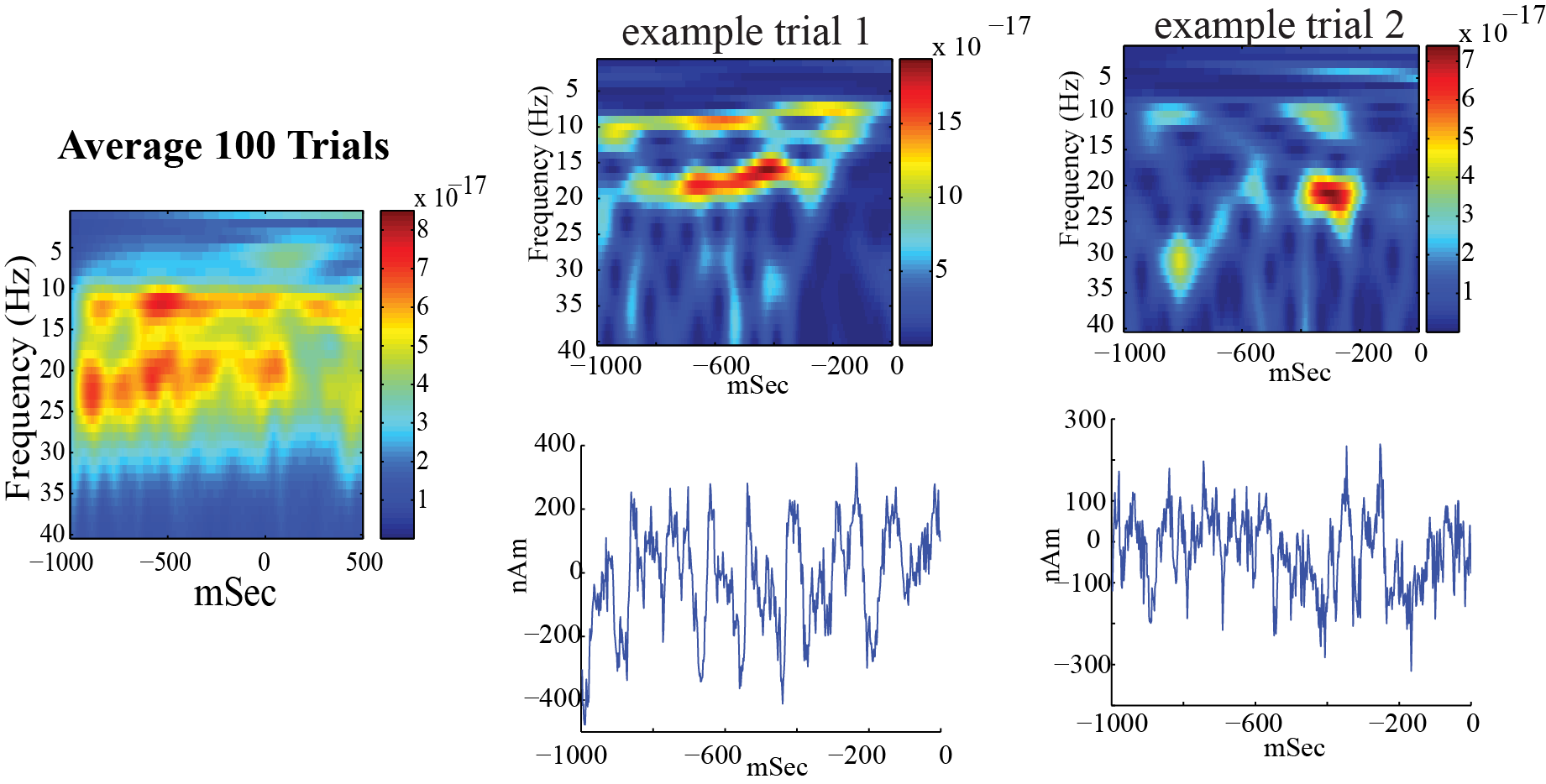 +
++Left: Spectrogram of spontaneous activity from current dipole +source in SI averaged across 100 trials, from an example subject, shows +nearly continuous prestimulus alpha and beta oscillations. At time zero, +a brief tap was given to the contralateral finger tip and the +spontaneous oscillations briefly desynchronized. +
++Right: A closer look at the prestimulus waveform and spectrogram +from spontaneous activity during example signal trials, shows that the +alpha and beta oscillations occur intermittently and primarily +non-overlapping. +
+ +Our goal was to use our neocortical model to reproduce features of +the waveform and spectrogram observed on single unaveraged trials +(Figure 2 top panel, right) where the alpha and beta components emerge +briefly and intermittently in time. On any individual trial (i.e., 1 +second of spontaneous data), the presence of alpha and beta activity is +not time locked and representative of so-called “induced” activity. +Seemingly continuous bands of activity occur only when averaging the +spectrograms across trials (Figure 2 top panel, left), and this is due +to the fact that the spectrograms values are strictly positive and the +alpha and beta events accumulate without cancellation [4].
+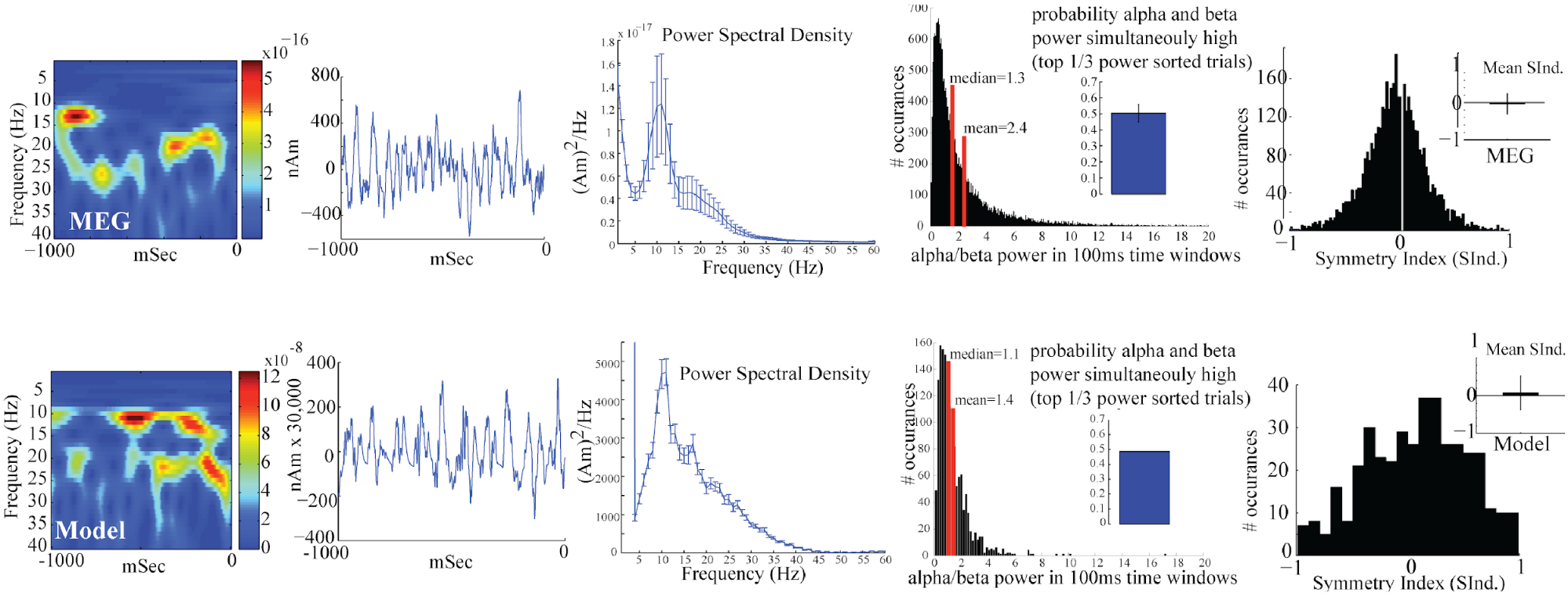 +
++Key features of the spontaneous non-average SI alpha/beta complex +include, intermittent transient bouts of alpha/beta activity, a waveform +that oscillates around 0nAm, PSD with peaks in the alpha and beta bands, +primarily non-overlapping alpha and beta events, and a symmetric +waveform oscillation. The model was able to reproduce each of these +features. +
+We found that a sequence of exogenous subthreshold excitatory +synaptic drive could activate the network in a manner that reproduced +important features of the SI rhythms in the model (Figure 2). This drive +consisted of two nearly-synchronous 10 Hz rhythmic drives that contacted +the network through proximal and distal projection pathways (Figure 3). +The drives were simulated as population “bursts” of action potentials +that contacted the network every 100ms with the mean delay between the +proximal and distal burst of 0ms. Specifically, as shown schematically +in Figure 3, the population bursts consisted of 10, 2-spike bursts +Gaussian distributed in time. We presumed that during such spontaneous +activity, these drives may be provided by leminscial and non-lemniscal +thalamic nuclei, which contact proximal and distal pyramidal neurons +respectively, and they are know to burst fire at ~10 Hz frequencies in +spontaneous states [5,6].
+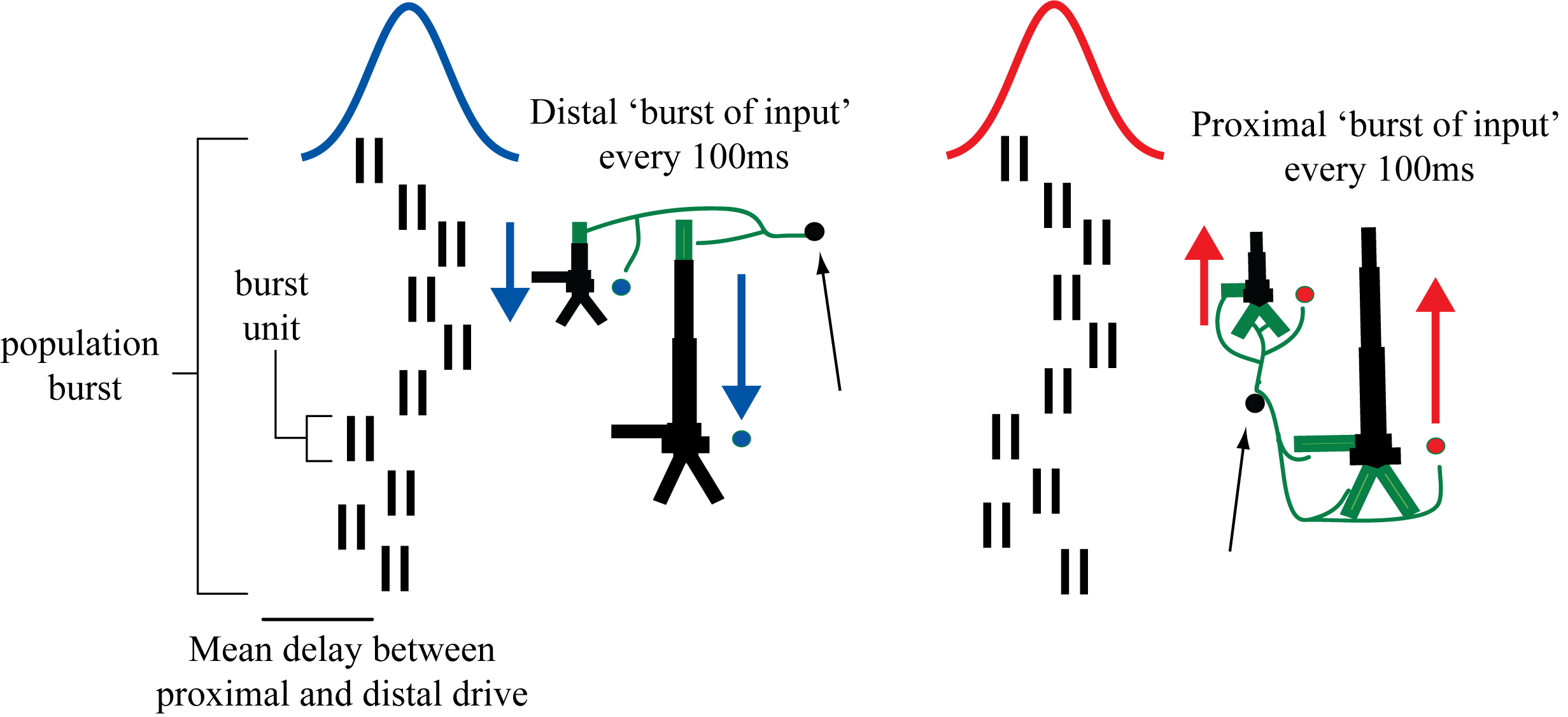 +
++Schematic illustration of exogenous 10 Hz burst drive through proximal +and distal projection pathways. “Population bursts”, consisting of a +set number of “burst units” (10, 2-spike bursts shown) drive +post-synaptic conductances in the local network with a set frequency +(100 ms ISI) and mean delay between proximal and distal. +
+We assumed that the macroscale rhythms generating the observed alpha +and beta activity arose from subthreshold current flow in a large +population of neurons, as opposed to being generated by local spiking +interaction. As such, the effective strengths of the exogenous driving +inputs were tuned so that the cells in the network remained subthreshold +(all other parameters were tuned and fixed base on the morphology, +physiology and connectivity within layered neocortical circuits, see +Jones et al. 2009 [1] for details). The inputs drove subthreshold +currents up and down the pyramidal neurons to reproduce accurate +waveform and spectrogram features (see Figure 3). A scaling factor of +3000 was multiplied by the model waveform to reproduce nAm units +comparable to the recorded data, suggesting on the order 200 x 3000 = +600,000 pyramidal neurons contributed to this signal.
+We further found that decreasing the delay between the drives to +~50ms created a pure alpha oscillation, while applying an ~0ms delay +caused beta events to emerge and increased the strength of the distal +drive, creating stronger beta activity (data not shown; see parameter +exploration below). This result led to the novel prediction that brief +beta events emerge from a broad proximal drive disrupted by a +simultaneous strong distal drive that lasted 50ms (i.e., one beta +period). Support for this prediction was found invasively with laminar +recordings in mice and monkeys [3].
+In this tutorial, we will explore parameter changes that illustrate +these results. We will walk you step-by-step through simulations with +various combinations of rhythmic proximal and distal drives to describe +how each contributes to the alpha and beta components of the SI +alpha/beta complex rhythm. We will begin by simulating only rhythmic +proximal alpha frequency inputs (Step 1), followed by simulating only +distal alpha frequency inputs (Step 2), followed by various combinations +of proximal and distal drive to generate alpha and beta rhythms. We’ll +show you how HNN can plot waveforms, time-frequency spectrograms, and +power spectral density plots of the simulated data, as well as for +imported recorded data.
+1. Simulating Rhythmic Proximal Inputs: Alpha +only
+2. Simulation Rhythmic Distal Inputs: Alpha +only
+3. Simulating Combined Rhythmic Proximal and +Distal Inputs: Alpha/Beta Complex
+4. Calculating and Viewing Power Spectral Density +(PSD)
+ + + + +6. Have fun exploring your own data!
+ + + + + + +Note that before running/loading new simulations, we will increase
+the run time of the simulation. Find the box labeled
+tstop (ms) under the Simulation tab and type
+in 700 as the value. This will enable us to see simulated
+oscillations as they evolve over longer time periods.
As described in the “Getting Started” section, low-frequency alpha +and beta rhythms can be simulated by a combination of rhythmic +subthreshold proximal and distal ~10Hz inputs. Here, we begin by +describing the impact of proximal inputs only. An initial parameter set +that will simulate the effect of ~10 Hz subthreshold proximal drive is +provided in the file OnlyRhythmicProx.json.
+The template cortical column networks structure for this simulation +is described in the Overview +and Under +the Hood sections. Several of the network parameter can be adjusted +via the HNN GUI (e.g. local excitatory and inhibitory connection +strengths), but we will leave them fixed for this tutorial and only +adjust the inputs the “activate” the network.
+To load the initial parameter set, navigate to the HNN GUI and click +the tab labeled:
+External drivesThen inside of the inside of the tab, click the button
+Load external drives (0)And select the file OnlyRhythmicProx.json from +HNN’s param subfolder or from your local machine.
+To view the parameters that “activate” the network via rhythmic +proximal input, click the dropdown menu labeled:
+bursty1 (proximal)You should see the values of adjustable parameters displayed as in +the dialog boxes below. There are 4 sections, one regulating the timing +statistics of the driving input, one regulating the post-synaptic +conductances onto the Layer 2/3 neurons, and one regulating the +post-synaptic conductances onto the Layer 5 neurons, and one regulating +the synaptic delays. We describe adjustable parameters in each dialog +box separately.
+ +Timing tab: The rhythmic proximal inputs drive excitatory synapses in
+the neocortical network in a proximal projection pattern, as shown at
+the bottom of the dialog box. For further details on the connectivity
+structure of the network, see the Under the Hoodsection of the HNN
+website. Rhythmic proximal input occurs through stochastic, presynaptic
+bursts of action potentials from a population of bursting cells (set
+with “Number bursts”; see Figure 3) onto postsynaptic neurons of the
+modelled network. Stochasticity is introduced in two places: the spike
+train start time for each bursting cell is sampled from a normal
+distribution with mean “Start time mean (ms)” and standard deviation
+“Start time stdev (ms)” and the inter-burst intervals for each bursting
+cell are sampled from a normal distribution of mean (e.g.,
+a 100 ms inter-burst interval corresponds to a “Burst frequency” of 10
+Hz) and standard deviation “Burst stdev (ms)” (see Figure 3). Also note
+that the number of spikes per burst unit is set with “Spikes/burst”
+(currently, only values of 1 and 2 with a fixed 10ms delay can be used)
+and the final stop time for the entire population of rhythmic proximal
+inputs is set with “Stop time (ms)”.
Layer 2/3, and Layer 5 tabs: This dialog box allows you to set the +postsynaptic conductance of each of the excitatory synapses in the +networks. There are AMPA and NMDA receptors on each cell type (pyramidal +and basket cells). There is also a delay parameter to control the +arrival time of each spike to the network. In this example, the delay to +the layer 2/3 cells is 0.1 ms, with a slightly longer delay to the layer +5 cells of 1 ms. For further details on the connectivity structure of +the network, see Under the Hood.
+To run this simulation, navigate to the main GUI window and +click:
+Start SimulationThis simulation runs for 700 ms of simulation time, so will take a +little longer to run than the ERP simulations. Once completed, you will +see output similar to that shown below.
+ + +As shown in the red histogram in the top panel of Figure 6 above, +with this parameter set, a burst of proximal input spikes is provided to +the network ~10 Hz (i.e., every 100 ms). Due to the stochastic nature of +the inputs (controlled by the start time stdev and Burst stdev +parameters, there is some variability in the histogram of proximal input +times. Note that a decrease in the Burst stdev would create shorter +duration bursts (i.e., more synchronous bursts); this will be explored +further in step 5.1 below.
+The ~10 Hz bursts of proximal drive induces current flow up the +pyramidal neuron dendrites increasing the signal above the 0 nAm +baseline, which then relaxes back to zero, approximately every 100 ms. +This is observed in the black current dipole waveform in the GUI +window.
+To view the time-frequency spectrogram for this waveform, click on
+the Visualization tab. Then click on the
+Layout template dropdown menu and select
+Drive-Dipole-Spectrogram. Finally click the
+Make Figure button.
The bottom panel shows the corresponding time-frequency spectrogram +for this waveform that exhibits a high-power continuous 10 Hz signal. +Importantly, in this example the strength of the proximal input was +titrated to be subthreshold (i.e., cells do not spike) under the +assumption that macroscale oscillations are generated primarily by +subthreshold current flow across large populations of synchronous +pyramidal neurons. In step 5.2 below, we explore differences in the +signal when the cells are driven to spike (see also ERP tutorial).
+To better see the 10 Hz signal, we can adjust the y-axis of the
+spectrogram. Under the options for ax2 which corresponds to
+the spectrogram on the bottom panel, change the values for
+Min Spectral Frequency (Hz) to 0.1 and
+Max Spectral Frequency (Hz) to 40.0.
Finally click Clear axis and then Add plot
+to regenerate the spectrogram. You should see the signal corresponding
+to the alpha rhthym much more clearly like in the figure below:
While this exploration with proximal drive is only useful in +understanding how subthreshold rhythmic inputs impact the current dipole +produced by the circuit, several features of the waveform and +spectrogram of the signal do not match the recorded data shown in +Figures 1 and 2. Next, we explore the impact of rhythmic distal inputs +only (step 2), and then a combination of the two (step 3).
+ +We will use a param file that generates bursts of distal inputs +provided at the alpha frequency (10 Hz; OnlyRhythmicDist.json).
+The template cortical column networks structure for this simulation +is described in the Overview and What’s Under the Hood sections. Several +of the network parameter can be adjusted via the HNN GUI (e.g. local +excitatory and inhibitory connection strengths), but we will leave them +fixed for this tutorial and only adjust the inputs the “activate” the +network.
+To load the initial parameter set, navigate to the HNN GUI and click +the tab labeled:
+External drivesThen inside of the inside of the tab, click the button
+Load external drives (0)Then select the file OnlyRhythmicDist.json from +HNN’s param subfolder or from your local machine.
+To view the parameters that “activate” the network via rhythmic +distal input, click the dropdown menu labeled:
+bursty2 (distal)You should see the values of adjustable parameters displayed as in +the dialog boxes below. Notice that these parameters are the same as +those regulating the proximal drive in step (1). However, in this case +the parameters define bursts of synaptic inputs that drive the network +in a distal project pattern, shown schematically at the bottom of the +dialog box.
+ +To run this simulation, navigate to the main GUI window and +click:
+Start SimulationOnce completed, you will see output similar to that shown below.
+ +As shown in the green histogram in the top panel of the HNN GUI +above, with this parameter set, a burst of distal input spikes is +provided to the network ~10 Hz (i.e., every 100 ms). Due to the +stochastic nature of the inputs (controlled by the start time stdev, and +Burst stdev parameters), there is some variability in the histogram of +proximal input times. The ~10 Hz bursts of distal input induces current +flow down the pyramidal neuron dendrites decreasing the signal below the +0 nAm baseline, which then relaxes back to zero, approximately every 100 +ms. This is observed in the black current dipole waveform in the GUI +window.
+Once again we will create time-frequency spectrogram for this
+waveform by first clicking on the Visualization tab. Then
+click on the Layout template dropdown menu and select
+Drive-Dipole-Spectrogram. Finally click the
+Make Figure button.
The bottom panel shows the corresponding time-frequency spectrogram +for this waveform that exhibits a high power continuous 10 Hz signal. +Importantly, in this example the strength of the distal input was also +titrated to be subthreshold (i.e., cells do not spike) under the +assumption that macroscale oscillations are generated primarily by +subthreshold current flow across large populations of synchronous +pyramidal neurons.
+While instructional, this simulation also does not produce waveform +and spectral features that match the experimental data in Figures +1 and 2. In the next step (step 3), we describe how combining both the +10 Hz proximal and distal drives can produce an oscillation with many +characteristic features of the spontaneous SI signal (Jones et al +2009).
+ +In this example, we provide a parameter set (AlphaAndBeta.json) +that produces many of the waveform and spectral features observed in our +SI data (Figure 2).
+The template cortical column networks structure for this simulation +is described in the Overview and What’s Under the Hood sections. Several +of the network parameter can be adjusted via the HNN GUI (e.g. local +excitatory and inhibitory connection strengths), but we will leave them +fixed for this tutorial and only adjust the inputs the “activate” the +network.
+To load the initial parameter set, navigate to the HNN GUI and click +the tab labeled:
+External drivesThen inside of the inside of the tab, click the button
+Load external drives (0)Then select the file AlphaAndBeta.json from +HNN’s param subfolder or from your local machine.
+To view the new parameters that “activate” the network via both +rhythmic proximal and rhythmic distal input, click the dropdown menus +labeled:
+bursty1 (proximal)
+bursty2 (distal)You should see the values displayed in the dialogue boxes below.
+ +In this simulation, the Start time mean (ms) values for both proximal +and distal inputs are set to 50.0 ms, and all other parameters are the +same. Note that the synaptic weights are the same as used in the +previous two simulations (not shown in dialog boxes above, click on +Layer 2/3 and Layer 5 to see them). The equal start time implies that +the proximal and distal input bursts will arrive nearly synchronously to +the network on each cycle of the 10 Hz input. Due to the stochasticity +in the parameters (start time stdev, and Burst stdev) sometimes the +bursts will arrive together and sometimes there will be a slight delay. +As will be described further below, this stochasticity creates +intermittent alpha and beta events.
+To run this simulation, navigate to the main GUI window by clicking
+the Simulation tab and then click:
RunOnce completed, you will see output similar to that shown below.
+
+ +
+
Follow the steps in the previous sections to create a time-frequency +spectrogram for this waveform. The output will look similar to the +figure below:
+ +As shown in the green and red histogram in the top panel of the HNN +GUI above, with this parameter set, bursts of both proximal and distal +input spikes are provided to the network ~10 Hz (i.e., every 100 ms). +Due to the stochastic nature of the inputs, there is some variability in +the timing and duration of the input bursts such that sometimes they +arrive at the same time and sometimes there is a slight offset between +them. As a result, intermittent transient alpha and beta events emerge +in the time-frequency spectrogram. Alpha events are produced when the +inputs occur slightly out of phase and current flow is pushed +alternately up and down the dendrites for ~50 ms duration each (set by +the length of the bursts inputs). Beta events occur when the burst +inputs arrive more synchronously and the upward current flow is +disrupted by downward current flow for ~50 ms to effectively cut the +oscillation period in half. As such, the relative alpha to beta +expression can be controlled by the delay between the inputs and their +relative burst strengths. We will detail this further below (see step 6 +below).
+In contrast to the results from only proximal or distal input, since +the current in the pyramidal neurons is pushed both upward and downward +in this simulation, the current dipole signal oscillates above and below +0 nAm, which qualitatively matches the experimental data (see Figures 1 +and 2 in “Getting Started”). Additionally, this simulation reproduces +the transient nature of the alpha and beta activity and several other +features of the waveform and spectrogram can be quantified to show close +agreement between model and experimental results (see Figure 2 above, +and Jones et al. 2009[1], for further details).
+We note that here we do not directly compare the spontaneous current +dipole waveform to recorded data, as was done in the ERP tutorial with a +root mean squared error. This is due to the fact that the spontaneous SI +signal we are simulating is not time locked to alpha or beta events on +any given trial, and the stochastic nature of the driving inputs causes +variability in the timing of the alpha or beta activity, making it +difficult to align recorded data and simulated results. However, a +direct comparison can be made between time averaged recorded and +simulated signals by comparing power spectral density waveforms. An +example of comparison is shown in step 5 below.
+As described in the “Getting Started” section above, our simulation +goal was to study the mechanisms that reproduce features of spontaneous +alpha and beta rhythms observed in un-averaged data, where the alpha and +beta components are transient and intermittent (Figure 1, right panel). +Each tutorial step up to this point was based on simulating un-averaged +data. Here, we describe how to run and average multiple “trials” (700 ms +epochs of spontaneous activity). We show that, due to the stochastic +nature of the proximal and distal rhythmic input, controlled by the +standard deviation (stdev) of the start times, and the stdev of the +input bursts), when running multiple trials, the precise timing of the +input bursts on each trial is jittered, and hence the alpha and beta +activity in the spectrograms on each trial is jittered. This is akin to +simulating induced rhythms rather than time-locked evoked rhythms. In +the averaged spectrogram across trials, the alpha and beta events +accumulate without cancellation (due to the fact that spectrogram value +are purely positive) creating the impression of a continuous oscillation +(Figure 1, left panel).
+Below we illustrate the effects of “jitter” in the proximal and +distal rhythmic inputs across trials in two ways. First, we examine the +effects of “jitter” due to the “Burst stdev”, and second due to the +“Start time stdev”.
+To first test the effects of jittering due to “Burst stdev” and +averaging across trials, we will use a param file (AlphaAndBetaJitter0.json) +with rhythmic proximal and distal inputs provided at 10 Hz, with +proximal and distal inputs in phase. These are the same parameters as in +the AlphaAndBeta.json file (Step 3.2 above), but now with 10 trials +instead of 1.
+To load the initial parameter set, navigate to the HNN GUI and click +the tab labeled:
+External drivesThen inside of the inside of the tab, click the button
+Load external drives (0)Then select the file OnlyRhythmicDist.json from +HNN’s param subfolder or from your local machine.
+To view the new parameters, click:
+bursty1 (proximal)
+bursty2 (distal)You should see the values displayed in the dialog boxes below.
+ +Notice that the Start time stdev (ms) is set to 0.0 for both proximal +and distal inputs, while the Burst stdev (ms) is 20.
+To run this simulation, navigate to the Simulation tab
+and click
RunThis simulation will take longer to run because it uses 10 trials. +Once completed, you will see output similar to that shown below.
+ +Follow the previous steps from section (1) or (2) to create a +time-frequency spectrogram. The output will look like the following:
+ +Notice that the input histograms for distal (green) and proximal +(red) input accumulated across the 10 trials, now have higher values +than before (up to ~20 compared to 5 in Step 3.2) and the burst inputs +are slightly broader on each cycle, since these histograms represent the +accumulated activity from 10 simulations, where the standard deviation +in the Burst duration across trials is 20 ms. Approximately 10 Hz +rhythmicity in the timing of the distal and proximal inputs can be +clearly visualized (note also the symmetric profile of the histograms). +However, on any individual trial, the coincidence of inputs leading to +alpha or beta events displays some variability due to the stochastic +parameter value (Burst stdev=20 ms). This is observed in the dipole +waveforms shown for each trial (example shown below).
+In the next simulation, we will jitter the start times of rhythmic +inputs across trials with the Start time stdev, in addition to a +non-zero Burst stdev. This will add additional variability to the timing +of the transient alpha and beta events on each trial, and hence produce +even more continuous bands of activity in the averaged spectrogram.
+First, navigate to the External drives tab and open the
+bursty1 (proximal) and bursty2 (distal)
+dropdown menus. Change the start time stdev from 0 ms to 50 ms in the
+timing tabs. The dialog boxes should now look as follows.
To run this simulation, click Start Simulation from the main GUI +window. Follow the steps from either section 1 or 2 to create a +time-frequency spectrogram
+Once completed, you will see output similar to that shown below.
+ +Notice that the input histograms for distal (green) and proximal +(red) input accumulated across the 10 trials now show little rhythmicity +due to the jitter in the rhythmic input start times across trials (Start +time stdv (ms) = 50), in addition to jitter due to the Burst stdev (ms) += 20. However, if we were to visualize histograms on each individual +trial (using the View spectrograms tab), they would show the ~10 Hz and +20 Hz (alpha and beta) rhythmicity. It is also difficult to visualize +rhythmicity in any of the overlaid dipole waveforms. However, on each +trial, alpha and beta rhythmicity is present, and even more continuous +bands of alpha and beta activity are observed (compare to averaged data +in Figure 1 left panel; n=100 trials) when the spectrograms from +individual trials are averaged. Running more trials will further +increase the continuous nature of alpha and beta activity across +time.
+Importantly, as stated above in this example the strength of the +proximal and distal input were titrated to be subthreshold (cells do not +spike) under the assumption that macroscale oscillations are generated +primarily by subthreshold current flow across large populations of +synchronous pyramidal neurons. We can verify the subthreshold nature of +the inputs by viewing the spiking activity in the network.
+Return to the single-trial parameter set as in Steps 3.1 and 3.2, by
+loading the AlphaAndBeta.json file and run the simulation. Then navigate
+to the Visualization tab, click the
+Layout template dropdown menu select
+Dipole-Spikes (2x1). Finally click
+Make figure.
You should see the following window.
+ +In this window, the rhythmic distal (green/top) and proximal +(red/middle) inputs bursts histograms are shown along with the spiking +activity in each population of cells (bottom panel). In this case, the +alpha and beta events are indeed produced through subthreshold processes +and there is no spiking produced in any cell in the network (no dots +present in the bottom raster plot).
+Try decreasing or increasing the number of trials in the above +simulations to see how these changes impact the continuity of alpha/beta +power over time. View some of the individual spectrograms to see that +alpha/beta are maintained on individual trials.
+ +HNN provides a feature to calculate and view the power spectral +density (PSD) of the simulated signal and imported data (Note: the PSD +is calculated as the time average of the spectrogram, in the simulation +examples).
+To calculate and view the PSD, navigate to the
+Visualization tab, click on the
+Layout template dropdown, and select
+PSD Layers (3x1)
You should see something similar to the following window.
+ +The PSD Viewer window shows the net current dipole (bottom panel) and +contribution from each layer in the network separately (top panels). +This example was run using the parameter set described in Step 3. PSD +from the simulation shows a strong peak in the alpha (~10 Hz) band, + with a lower peak power in beta band (~20 Hz).
+ + + + +Parameter adjustments will be key to developing and testing +hypotheses on the circuit origin of your own low-frequency rhythmic +data. HNN is designed so that many of the parameters in the model can be +adjusted from the GUI (see the Tour of the GUI tutorial).
+Here, we’ll walk through examples of how to adjust several “Rhythmic +Proximal/Distal Input” parameters to investigate how they impact the +alpha and beta rhythms described above. We end with some suggested +exercises for further exploration.
+We described above (Step 3) that the timing of proximal and distal +inputs can lead to either alpha events (when the bursts arrive to the +local network out of phase) or beta events (when the bursts arrive in +phase).
+We have also found that other factors that contribute to the +prevalence of beta activity are the strengthand synchrony of the distal +inputs; beta activity is increased with stronger and more synchronous +subthreshold drive, where the beta frequency is set by the duration of +the driving bursts (~50ms) (Jones et al. 2009; Sherman et al. 2016). The +strength is controlled by the postsynaptic conductance, and the +synchrony is controlled by the Burst stdev in the “Rhythmic Distal +Inputs” dialog box. We will demonstrate this here.
+Open the External drives tab and click on the dropdown
+menu bursty2 (distal)
Reduce the Burst stdev (Hz) value from 20 ms to 10 ms. This will
+create higher synchrony in the timing of the distal input bursts. Under
+both the Layer 2/3 and Layer 5 tabs, increase the postsynaptic condances
+weights of the AMPA synapses onto the Layer 2/3 and Layer 5 pyramidal
+neurons from 5.4e-5 to
+6e-5
.
+Both of these changes will cause the distal input burst to push a
+greater amount of current flow down the pyramidal neuron dendrites. The
+“Rhythmic Distal Input” dialog windows should look as shown below.
Next, we will test how these parameter changes affect the simulation.
+Select the Simulation tab and click the Run
+button. Then follow the steps from section 1 or 2 to create a
+time-frequency spectrogram Once completed, you will see output in the
+GUI similar to that shown below.
First, notice that the histogram profile of the distal input bursts +(green) are narrower corresponding to more synchronous input than in the +prior simulation (Step 3). Second, notice that the waveform of the +oscillation is different with a sharper downward deflecting signal, due +to to the stronger distal input. These deflections increased ~20 Hz beta +activity, as seen in the corresponding spectrogram (compare to +spectrogram in Step 3). The 20 Hz frequency is set by the duration of +the downward current flow, which with this parameter set is +approximately 50 ms (see Sherman et al. 2016[3] for further +details).
+Try changing the frequency of the rhythmic distal drive from 10 Hz to +20 Hz. Try other frequencies for the proximal and distal rhythmic drive. +How do the rhythms change? See how changes in the Burst stdev effects +the rhythms expressed.
+Recall that in the above simulations, the strength of the rhythmic +proximal and distal inputs were chosen so that the cells remained +subthreshold (no spiking). We will now demonstrate what happens if we +increase the strength of the inputs far enough to induce spikes. Instead +of simulating subthreshold alpha/beta events, we will see that the +dipole signals are dominated by higher-frequency events created by +spiking activity. We note that the produced waveforms of activity are, +to our knowledge, not typically observed in MEG or EEG data, supporting +the notion that alpha/beta rhythms are created through subthreshold +processes.
+To test this, select the External drives tab, open the
+bursty2 (distal) dropdown menu, and change the parameters
+as follows. Under the timing tab, change the Burst stdev value back to
+20 ms. Under both the Layer 2/3 and Layer 5 tabs, increase the
+postsynaptic conductance weights of the AMPA synapses onto the Layer 2/3
+and Layer 5 pyramidal neurons from 6e-5 to
+40e-5
(a
+big change that will provide enough current to cause the cells to
+spike). The “Rhythmic Distal Input” dialog windows should look as shown
+below.
Next, run the simulation. Click on Start Simulation from the main GUI +window. Once completed, you will see output similar to that shown +below.
+ +Notice that the histogram profile of the distal input bursts (green)
+are once again wider corresponding to less synchronous input and
+comparable to those shown in the example in Step 3. However, in this
+case the postsynaptic conductance of these driving spike is
+significantly larger (40e-5 ).
+This strong input induces spiking activity in the pyramidal neuron on
+several cycles of the drive (2.5 shown here) resulting in a sharp and
+rapidly oscillating dipole waveform. The corresponding dipole
+spectrogram shows broadband spiking from ~60-120 Hz. This type of
+activity is not typically seen in EEG or MEG data, and hence unlikely to
+underlie macroscale recordings.
We can verify that the neurons are spiking by looking at the spiking
+raster plots. To do so, navigate to Visualization tab,
+click the Layout template dropdown menu and select
+PSD Layers (3x1). Then click Make figure.
Notice that highly synchronous neuronal spiking in each population +coincides with the high-frequency events seen in the waveform and +spectrogram. The waveform response is induced by the pyramidal neuron +spiking which creates rapid back-propagating action potentials and +repolarization of the dendrites.
+Hypothesis testing:This simulation demonstrates that HNN can be used +to test the limits of physiological variables and to see how, as +parameters are varied, simulations results can be similar or dissimilar +to experimental data.
+View the contribution of Layer 2/3 and Layer 5 to the net current +dipole waveform and compare with the spiking activity in each +population. How do each contribute? Try also to change the proximal +input parameters instead of the distal input parameters.
+Adjust one of the parameter regulating the local network connections. +What happens?
+We mentioned above that, in addition to parameters controlling the
+strength and synchrony of the distal (or proximal) drive, the relative
+timing of proximal and distal inputs is an important factor in
+determining relative alpha and beta expression in the model. Here we
+will demonstrate that out-of-phase, 10 Hz burst inputs can produce
+continuous alpha activity without any beta events. For this simulation,
+load the AlphaAndBeta.json parameter
+file as described in Step 3 by clicking Set Parameters From File and
+selecting the file from HNN’s param subfolder. To view the new
+parameters, click on the External drives tab. Next, in the
+bursty1 (proximal) dropdown menu, change the start time
+mean from 50 to 100 ms. The timing tabs in the Rhythmic Proximal and
+Distal Input dialog boxes should look as follows:
Note that both the proximal and distal input frequency are set to 10 +Hz (bursts of activity every ~100 ms). Since the proximal input Start +time mean is 50.0 ms and the the distal input Start time mean is 100.0 +ms, the input will, on average, arrive to the network a 1/2 cycle out of +phase (i.e., in antiphase, every 50 ms).
+Next, we will run the simulation to investigate the impact of this +parameter change. Click on Start Simulation from the main GUI window. +Once completed, you will see output similar to that shown below.
+ + +Notice that the histogram profile of the proximal (red) and distal +(green) input bursts are generally ½ cycle out-of-phase (antiphase). +This rhythmic alteration of proximal followed by distal drive induces +alternating subthreshold current flow up and down the pyramidal neuron +dendrites to create a continuous alpha oscillation in the current dipole +waveform that oscillates around 0 nAm. The period of the oscillation is +set by the duration of each burst (~50 ms, controlled in part by Burst +stdev) and the 50 ms delay between the inputs on each cycle (due to +different start times). The corresponding spectrogram shows continuous +nearly pure alpha activity. This type of strong alpha activity is +similar to what might be observed over occipital cortex during eyes +closed conditions.
+Try changing the delay between the proximal and distal drive by +varying amounts. What happens to the rhythm expressed?
+Can you create a simulation where other frequencies are expressed? +How is it created? Are the cells spiking or subthreshold?
+ +Follow steps 1-5 above using your data and parameter adjustments +based on your own hypotheses.
+Jones, +S. R. et +al.Quantitative +analysis and biophysically realistic neural modeling of the MEG mu +rhythm: rhythmogenesis and modulation of sensory-evoked responses. +J. +Neurophysiol. 102, 3554–3572 +(2009).
Ziegler, +D. A. et +al.Transformations +in oscillatory activity and evoked responses in primary somatosensory +cortex in middle age: a combined computational neural modeling and MEG +study. Neuroimage 52, 897–912 +(2010).
Sherman, +M. A. et +al.Neural +mechanisms of transient neocortical beta rhythms: Converging evidence +from humans, computational modeling, monkeys, and mice. Proc. +Natl. Acad. Sci. U. S. A. 113, E4885–94 +(2016).
Jones, +S. R. When brain rhythms aren’t ‘rhythmic’: implication for their +mechanisms and meaning. Curr. +Opin. Neurobiol. 40, 72–80 +(2016).
Jones, +E. G. The thalamic matrix and thalamocortical synchrony. Trends +Neurosci. 24, 595–601 +(2001).
Hughes, +S. W. & Crunelli, V. Thalamic mechanisms of EEG alpha rhythms and +their pathological implications. Neuroscientist 11, 357–372 +(2005).
Left: Spectrogram of spontaneous activity from current dipole source in SI averaged across 100 trials, from an example subject, shows nearly continuous prestimulus alpha and beta oscillations. At time zero, a brief tap was given to the contralateral finger tip and the spontaneous oscillations briefly desynchronized.
-Right: A closer look at the prestimulus waveform and spectrogram from spontaneous activity during example signal trials, shows that the alpha and beta oscillations occur intermittently and primarily non-overlapping. +
Right: A closer look at the prestimulus waveform and spectrogram from spontaneous activity during example signal trials, shows that the alpha and beta oscillations occur intermittently and primarily non-overlapping.
 +
+
 +
+
 +
+
 +
+
 +
+
 +
+
- +
+
|
- +
+
|
- +
+
|
- +
+
|
- +
+
|
- +
+
|
- +
+
|
- +
+
|
- +
+
|
- +
+
|
-
|
-
|