文章核心思想
- 在大规模的推荐系统中,利用双塔模型对user-item对的交互关系进行建模,学习
${user,context}$ 向量与${item}$ 向量. - 针对大规模流数据,提出in-batch softmax损失函数与流数据频率估计方法(Streaming Frequency Estimation),可以更好的适应item的多种数据分布。
文章主要贡献
-
提出了改进的流数据频率估计方法:针对流数据来估计item出现的频率,利用实验分析估计结果的偏差与方差,模拟实验证明该方法在数据动态变化时的功效
-
提出了双塔模型架构:提供了一个针对大规模的检索推荐系统,包括了 in-batch softmax 损失函数与流数据频率估计方法,减少了负采样在每个batch中可能会出现的采样偏差问题。
给定一个查询集 $Query: \left{x_{i}\right}{i=1}^{N}$ 和一个物品集$Item:\left{y{j}\right}_{j=1}^{M}$。
-
$x_{i} \in X,\quad y_{j} \in \mathcal{Y}$ 是由多种特征(例如:稀疏ID和 Dense 特征)组成的高维混合体。 -
推荐的目标是对于给定一个
$query$ ,检索到一系列$item$ 子集用于后续排序推荐任务。
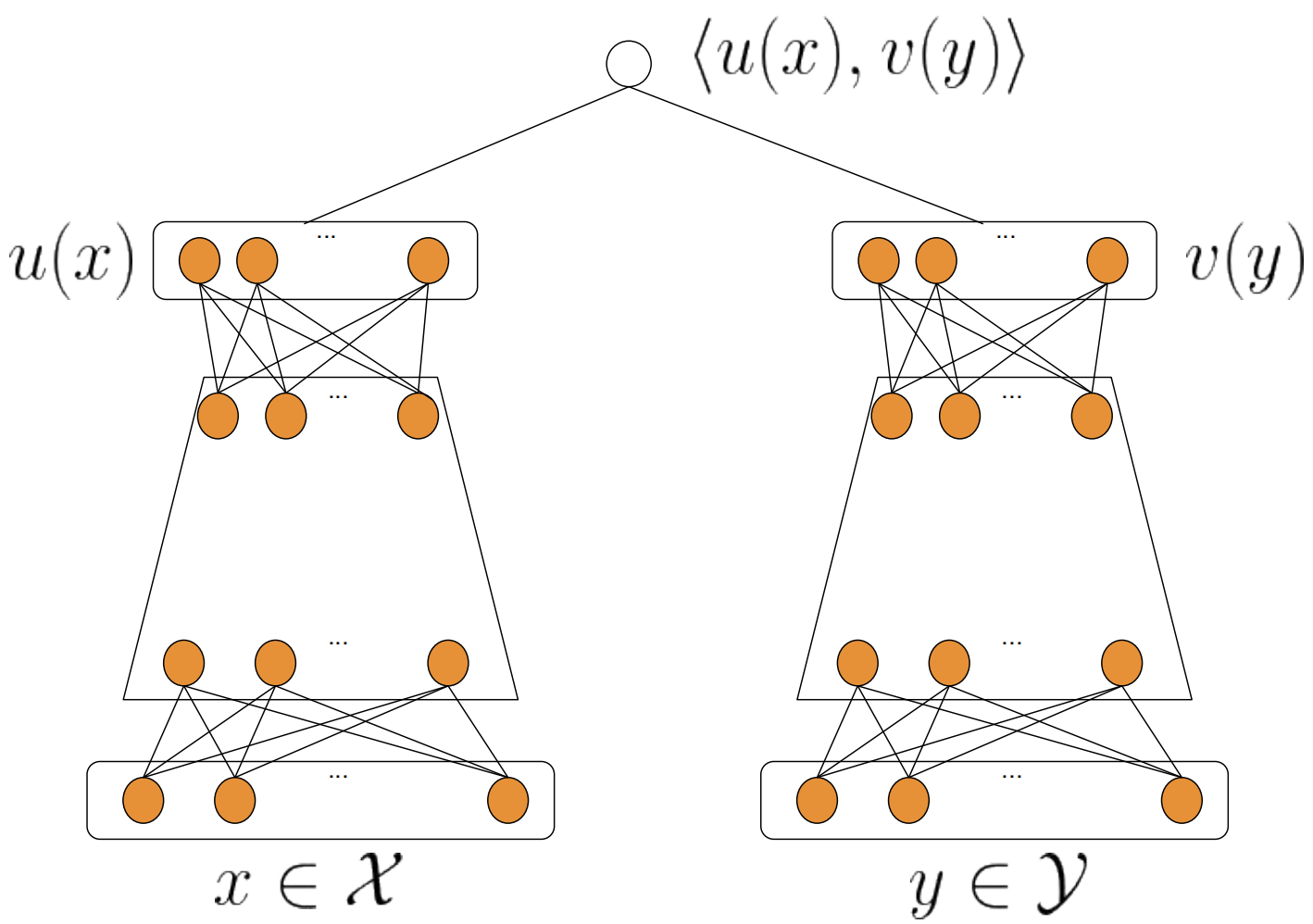
模型结构如上图所示,论文旨在对用户和物品建立两个不同的模型,将它们投影到相同维度的空间: $$ u: X \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{k}, v: y \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{k} $$
模型的输出为用户与物品向量的内积:
模型的目标是为了学习参数
- 在推荐系统中,$r_i$ 可以扩展来捕获用户对不同候选物品的参与度。
- 例如,在新闻推荐中
$r_i$ 可以是用户在某篇文章上花费的时间。
-
给定用户
$x$ ,基于 softmax 函数从物料库$M$ 中选中候选物品$y$ 的概率为: $$ \mathcal{P}(y \mid x ; \theta)=\frac{e^{s(x, y)}}{\sum_{j \in[M]} e^{s\left(x, y_{j}\right)}} $$-
考虑到相关奖励
$r_i$ ,加权对数似然函数的定义如下:$$ L_{T}(\theta):=-\frac{1}{T} \sum_{i \in[T]} r_{i} \cdot \log \left(\mathcal{P}\left(y_{i} \mid x_{i} ; \theta\right)\right) $$
-
-
原表达式
$\mathcal{P}(y \mid x ; \theta)$ 中的分母需要遍历物料库中所有的物品,计算成本太高,故对分母中的物品要进行负采样。为了提高负采样的速度,一般是直接从训练样本所在 Batch 中进行负样本选择。于是有: $$ \mathcal{P}{B}\left(y{i} \mid x_{i} ; \theta\right)=\frac{e^{s\left(x_{i}, y_{i}\right)}}{\sum_{j \in[B]} e^{s\left(x_{i}, y_{j}\right)}} $$- 其中,$B$ 表示与样本
${x_i,y_j}$ 同在一个 Batch 的物品集合。 - 举例来说,对于用户1,Batch 内其他用户的正样本是用户1的负样本。
- 其中,$B$ 表示与样本
-
一般而言,负采样分为 Easy Negative Sample 和 Hard Negative Sample。
-
这里的 Easy Negative Sample 一般是直接从全局物料库中随机选取的负样本,由于每个用户感兴趣的物品有限,而物料库又往往很大,故即便从物料库中随机选取负样本,也大概率是用户不感兴趣的。
-
在真实场景中,热门物品占据了绝大多数的购买点击。而这些热门物品往往只占据物料库物品的少部分,绝大部分物品是冷门物品。
- 在物料库中随机选择负样本,往往被选中的是冷门物品。这就会造成马太效应,热门物品更热,冷门物品更冷。
- 一种解决方式时,在对训练样本进行负采样时,提高热门物品被选为负样本的概率,工业界的经验做法是物品被选为负样本的概率正比于物品点击次数的 0.75 次幂。
-
前面提到 Batch 内进行负采样,热门物品出现在一个 Batch 的概率正比于它的点击次数。问题是,热门物品被选为负样本的概率过高了(一般正比于点击次数的 0.75 次幂),导致热门物品被过度打压。
-
在本文中,为了避免对热门物品进行过度惩罚,进行了纠偏。公式如下: $$ s^{c}\left(x_{i}, y_{j}\right)=s\left(x_{i}, y_{j}\right)-\log \left(p_{j}\right) $$
- 在内积
$s(x_i,y_j)$ 的基础上,减去了物品$j$ 的采样概率的对数。
- 在内积
-
-
纠偏后,物品
$y$ 被选中的概率为: $$ \mathcal{P}{B}^{c}\left(y{i} \mid x_{i} ; \theta\right)=\frac{e^{s^{c}\left(x_{i}, y_{i}\right)}}{e^{s^{c}\left(x_{i}, y_{i}\right)}+\sum_{j \in[B], j \neq i} e^{s^{c}\left(x_{i}, y_{j}\right)}} $$- 此时,batch loss function 的表示式如下:
$$ L_{B}(\theta):=-\frac{1}{B} \sum_{i \in[B]} r_{i} \cdot \log \left(\mathcal{P}{B}^{c}\left(y{i} \mid x_{i} ; \theta\right)\right) $$
- 通过 SGD 和学习率,来优化模型参数
$\theta$ :
$$ \theta \leftarrow \theta-\gamma \cdot \nabla L_{B}(\theta) $$
-
Normalization and Temperature
-
最后一层,得到用户和物品的特征 Embedding 表示后,再进行进行
$l2$ 归一化: $$ \begin{aligned} u(x, \theta) \leftarrow u(x, \theta) /|u(x, \theta)|{2} \ v(y, \theta) \leftarrow v(y, \theta) /|v(y, \theta)|{2}\end{aligned} $$
- 本质上,其实就是将用户和物品的向量内积转换为了余弦相似度。
-
对于内积的结果,再除以温度参数
$\tau$ : $$ s(x, y)=\langle u(x, \theta), v(y, \theta)\rangle / \tau $$- 论文提到,这样有利于提高预测准确度。
- 从实验结果来看,温度参数
$\tau$ 一般小于$1$ ,所以感觉就是放大了内积结果。
-
上述模型训练过程可以归纳为:
(1)从实时数据流中采样得到一个 batch 的训练样本。
(2)基于流频估计法,估算物品
(3)计算损失函数
考虑一个随机的数据 batch ,每个 batch 中包含一组物品。现在的问题是如何估计一个 batch 中物品
- 利用全局步长,将对物品采样频率
$p$ 转换为 对$\delta$ 的估计,其中$\delta$ 表示连续两次采样物品之间的平均步数。 - 例如,某物品平均 50 个步后会被采样到,那么采样频率
$p=1/\delta=0.02$ 。
具体的实现方法为:
-
建立两个大小为
$H$ 的数组$A,B$ 。 -
通过哈希函数
$h(\cdot)$ 可以把每个物品映射为$[H]$ 范围内的整数。-
映射的内容可以是 ID 或者其他的简单特征值。
-
对于给定的物品
$y$ ,哈希后的整数记为$h(y)$ ,本质上它表示物品$y$ 在数组中的序号。
-
-
数组
$A$ 中存放的$A[h(y)]$ 表示物品$y$ 上次被采样的时间, 数组$B$ 中存放的$B[h(y)]$ 表示物品$y$ 的全局步长。-
假设在第
$t$ 步时采样到物品$y$ ,则$A[h(y)]$ 和$B[h(y)]$ 的更新公式为: $$ B[h(y)] \leftarrow(1-\alpha) \cdot B[h(y)]+\alpha \cdot(t-A[h(y)]) $$ -
在$B$ 被更新后,将
$t$ 赋值给$A[h(y)]$ 。
-
-
对整个batch数据采样后,取数组
$B$ 中$B[h(y)]$ 的倒数,作为物品$y$ 的采样频率,即: $$ \hat{p}=1 / B[h(y)] $$
从数学理论上证明这种迭代更新的有效性:
假设物品
-
对于均值的证明: $$ \begin{aligned} E\left[\delta_{t}\right] &=(1-\alpha) E\left[\delta_{t-1}\right]+\alpha \delta \ &=(1-\alpha)\left[(1-\alpha) E\left[\delta_{t-2}\right]+\alpha \delta\right]+\alpha \delta \ &=(1-\alpha)^{2} E\left[\delta_{t-2}\right]+\left[(1-\alpha)^{1}+(1-\alpha)^{0}\right] \alpha \delta \ &=(1-\alpha)^{3} E\left[\delta_{t-3}\right]+\left[(1-\alpha)^{2}+(1-\alpha)^{1}+(1-\alpha)^{0}\right] \alpha \delta \ &=\ldots \ldots \ &=(1-\alpha)^{t} \delta_{0}+\left[(1-\alpha)^{t-1}+\ldots+(1-\alpha)^{1}+(1-\alpha)^{0}\right] \alpha \delta \ &=(1-\alpha)^{t} \delta_{0}+\left[1-(1-\alpha)^{t-1}\right] \delta \end{aligned} $$
- 根据均值公式可以看出:$t \rightarrow \infty \text { 时, }\left|E\left[\delta_{t}\right]-\delta\right| \rightarrow 0 $ 。
- 即当采样数据足够多的时候,数组
$B$ (每多少步采样一次)趋于真实采样频率。 - 因此递推式合理,且当初始值
$\delta_{0}=\delta /(1-\alpha)$ ,递推式为无偏估计。
-
对于方差的证明: $$ \begin{aligned} E\left[\left(\delta_{t}-E\left[\delta_{t}\right]\right)^{2}\right] &=E\left[\left(\delta_{t}-\delta+\delta-E\left[\delta_{t}\right]\right)^{2}\right] \ &=E\left[\left(\delta_{t}-\delta\right)^{2}\right]+2 E\left[\left(\delta_{t}-\delta\right)\left(\delta-E\left[\delta_{t}\right]\right)\right]+\left(\delta-E\left[\delta_{t}\right]\right)^{2} \ &=E\left[\left(\delta_{t}-\delta\right)^{2}\right]-\left(E\left[\delta_{t}\right]-\delta\right)^{2} \ & \leq E\left[\left(\delta_{t}-\delta\right)^{2}\right] \end{aligned} $$
-
对于
$E\left[\left(\delta_{i}-\delta\right)^{2}\right]$ : $$ \begin{aligned} E\left[\left(\delta_{i}-\delta\right)^{2}\right] &=E\left[\left((1-\alpha) \delta_{i-1}+\alpha \Delta_{i}-\delta\right)^{2}\right] \ &=E\left[\left((1-\alpha) \delta_{i-1}+\alpha \Delta_{i}-(1-\alpha+\alpha) \delta\right)^{2}\right] \ &=E\left[\left((1-\alpha)\left(\delta_{i-1}-\delta\right)+\alpha\left(\Delta_{i}-\delta\right)\right)^{2}\right] \ &=(1-\alpha)^{2} E\left[\left(\delta_{i-1}-\delta\right)^{2}\right]+\alpha^{2} E\left[\Delta_{i}-\delta\right]^{2}+2 \alpha(1-\alpha) E\left[\left(\delta_{i-1}-\delta\right)\left(\Delta_{i}-\delta\right)\right] \end{aligned} $$ -
由于
$\delta_{i-1}$ 和$\Delta_{i}$ 独立,所以上式最后一项为 0,因此: $$ E\left[\left(\delta_{i}-\delta\right)^{2}\right]=(1-\alpha)^{2} E\left[\left(\delta_{i-1}-\delta\right)^{2}\right]+\alpha^{2} E\left[\Delta_{i}-\delta\right]^{2} $$ -
与均值的推导类似,可得: $$ \begin{aligned} E\left[\left(\delta_{t}-\delta\right)^{2}\right] &=(1-\alpha)^{2 t}\left(\delta_{0}-\delta\right)^{2}+\alpha^{2} \frac{1-(1-\alpha)^{2 t-2}}{1-(1-\alpha)^{2}} E\left[\left(\Delta_{1}-\delta\right)^{2}\right] \ & \leq(1-\alpha)^{2 t}\left(\delta_{0}-\delta\right)^{2}+\alpha E\left[\left(\Delta_{1}-\delta\right)^{2}\right] \end{aligned} $$
-
由此可证明: $$ E\left[\left(\delta_{t}-E\left[\delta_{t}\right]\right)^{2}\right] \leq(1-\alpha)^{2 t}\left(\delta_{0}-\delta\right)^{2}+\alpha E\left[\left(\Delta_{1}-\alpha\right)^{2}\right] $$
-
- 对于方差,上式给了一个估计方差的上界。
上述流动采样频率估计算法存在的问题:
-
对于不同的物品,经过哈希函数映射的整数可能相同,这就会导致哈希碰撞的问题。
-
由于哈希碰撞,对导致对物品采样频率过高的估计。
解决方法:
- 使用
$m$ 个哈希函数,取$m$ 个估计值中的最大值来表示物品连续两次被采样到之间的步长。
具体的算法流程:
-
分别建立
$m$ 个大小为$H$ 的数组 ${A}{i=1}^{m}$,${B}{i=1}^{m}$,一组对应的独立哈希函数集合${h}_{i=1}^{m}$ 。 -
通过哈希函数
$h(\cdot)$ 可以把每个物品映射为$[H]$ 范围内的整数。对于给定的物品$y$ ,哈希后的整数记为$h(y)$ -
数组
$A_i$ 中存放的$A_i[h(y)]$ 表示在第$i$ 个哈希函数中物品$y$ 上次被采样的时间。数组$B_i$ 中存放的$B_i[h(y)]$ 表示在第$i$ 个哈希函数中物品$y$ 的全局步长。 -
假设在第
$t$ 步采样到物品$y$ ,分别对$m$ 个哈希函数对应的$A[h(y)]$ 和$B[h(y)]$ 进行更新: $$ \begin{aligned} & B_i[h(y)] \leftarrow(1-\alpha) \cdot B_i[h(y)]+\alpha \cdot(t-A_i[h(y)])\ \ & A_i[h(y)]\leftarrow t \end{aligned} $$ -
对整个 batch 数据采样后,取
${B}_{i=1}^{m}$ 中最大的$B[h(y)]$ 的倒数,作为物品$y$ 的采样频率,即:
$$ \hat{p}=1 / \max {i}\left{B{i}[h(y)]\right} $$
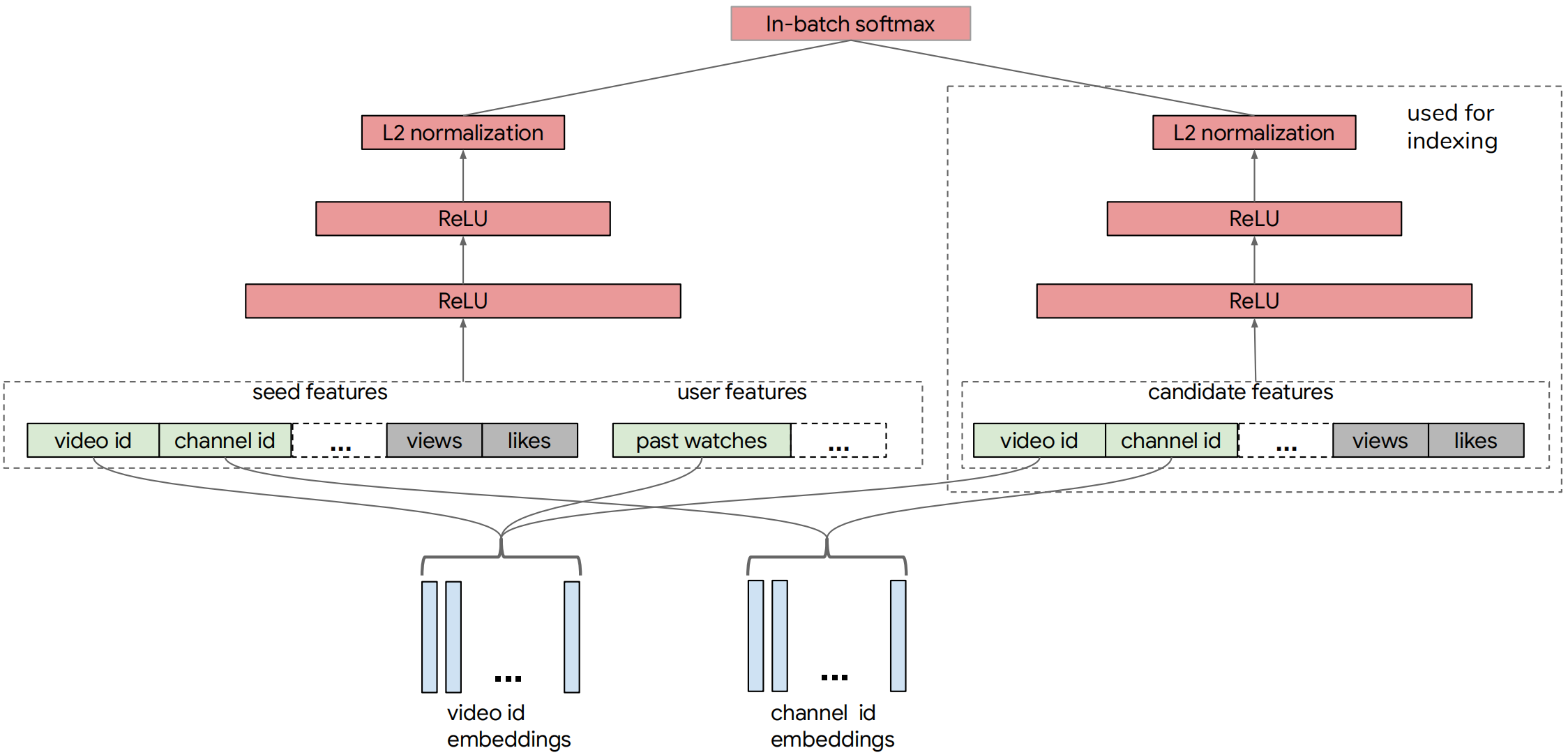
本文构建的 YouTube 神经检索模型由查询和候选网络组成。下图展示了整体的模型架构。
在任何时间点,用户正在观看的视频,即种子视频,都会提供有关用户当前兴趣的强烈信号。因此,本文利用了大量种子视频特征以及用户的观看历史记录。候选塔是为了从候选视频特征中学习而构建的。
-
Training Label
- 视频点击被用作正面标签。对于每次点击,我们都会构建一个 rewards 来反映用户对视频的不同程度的参与。
-
$r_i$ = 0:观看时间短的点击视频;$r_i$ = 1:表示观看了整个视频。
-
Video Features
-
YouTube 使用的视频特征包括 categorical 特征和 dense 特征。
- 例如 categorical 特征有 video id 和 channel id 。
- 对于 categorical 特征,都会创建一个嵌入层以将每个分类特征映射到一个 Embedding 向量。
- 通常 YouTube 要处理两种类别特征。从原文的意思来看,这两类应该是 one-hot 型和 multi-hot 型。
-
-
User Features
- 使用用户观看历史记录来捕捉 seed video 之外的兴趣。将用户最近观看的 k个视频视为一个词袋(BOW),然后将它们的 Embedding 平均。
- 在查询塔中,最后将用户和历史 seed video 的特征进行融合,并送入输入前馈神经网络。
-
类别特征的 Embedding 共享
- 原文:For the same type of IDs, embeddings are shared among the related features. For example, the same set of video id embeddings is used for seed, candidate and users past watches. We did experiment with non-shared embeddings, but did not observe significant model quality improvement.
- 大致意思就是,对于相同 ID 的类别,他们之间的 Embedding 是共享的。例如对于 seed video,出现的地方包括用户历史观看,以及作为候选物品,故只要视频的 ID 相同,Embedding也是相同的。如果不共享,也没啥提升。