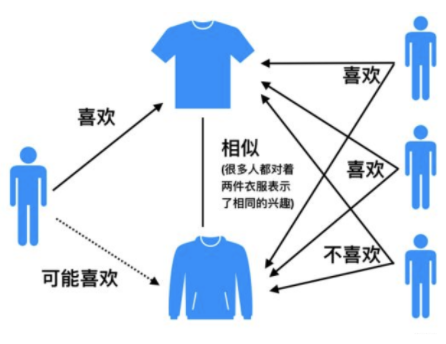
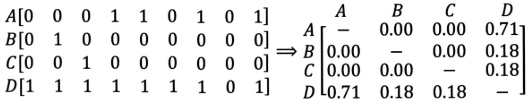基于物品的协同过滤(ItemCF):
- 预先根据所有用户的历史行为数据,计算物品之间的相似性。
- 然后,把与用户喜欢的物品相类似的物品推荐给用户。
举例来说,如果用户 1 喜欢物品 A ,而物品 A 和 C 非常相似,则可以将物品 C 推荐给用户1。ItemCF算法并不利用物品的内容属性计算物品之间的相似度, 主要通过分析用户的行为记录计算物品之间的相似度, 该算法认为, 物品 A 和物品 C 具有很大的相似度是因为喜欢物品 A 的用户极可能喜欢物品 C。
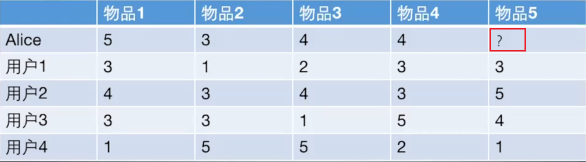
基于物品的协同过滤算法和基于用户的协同过滤算法很像, 所以我们这里直接还是拿上面 Alice 的那个例子来看。
如果想知道 Alice 对物品5打多少分, 基于物品的协同过滤算法会这么做:
-
首先计算一下物品5和物品1, 2, 3, 4之间的相似性。
-
在Alice找出与物品 5 最相近的 n 个物品。
-
根据 Alice 对最相近的 n 个物品的打分去计算对物品 5 的打分情况。
手动计算:
-
手动计算物品之间的相似度
物品向量:
$物品 1(3,4,3,1) ,物品2(1,3,3,5) ,物品3(2,4,1,5) ,物品4(3,3,5,2) ,物品5(3,5,41)$ -
下面计算物品 5 和物品 1 之间的余弦相似性: $$ \operatorname{sim}(\text { 物品1, 物品5 })=\operatorname{cosine}(\text { 物品1, 物品5 } )=\frac{9+20+12+1}{\operatorname{sqrt}(9+16+9+1)+\operatorname{sqrt}(9+25+16+1)} $$
-
皮尔逊相关系数类似。
-
-
基于
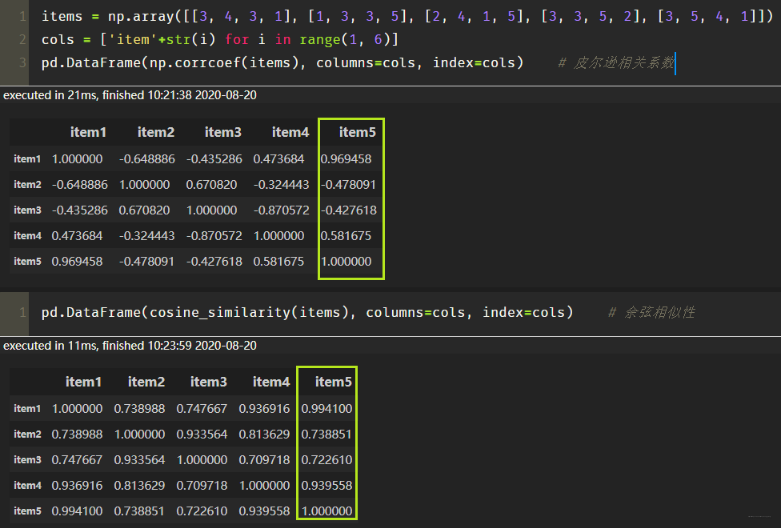
sklearn计算物品之间的皮尔逊相关系数:
- 根据皮尔逊相关系数, 可以找到与物品5最相似的2个物品是 item1 和 item4, 下面基于上面的公式计算最终得分:
$$ P_{Alice, 物品5}=\bar{R}{物品5}+\frac{\sum{k=1}^{2}\left(w_{物品5,物品 k}\left(R_{Alice, 物品k}-\bar{R}{物品k}\right)\right)}{\sum{k=1}^{2} w_{物品k, 物品5}} \ =\frac{13}{4}+\frac{0.97*(5-3.2)+0.58*(4-3.4)}{0.97+0.58}=4.6 $$
-
构建物品-用户的评分矩阵
import numpy as np import pandas as pd def loadData(): items = {'A': {'Alice': 5.0, 'user1': 3.0, 'user2': 4.0, 'user3': 3.0, 'user4': 1.0}, 'B': {'Alice': 3.0, 'user1': 1.0, 'user2': 3.0, 'user3': 3.0, 'user4': 5.0}, 'C': {'Alice': 4.0, 'user1': 2.0, 'user2': 4.0, 'user3': 1.0, 'user4': 5.0}, 'D': {'Alice': 4.0, 'user1': 3.0, 'user2': 3.0, 'user3': 5.0, 'user4': 2.0}, 'E': {'user1': 3.0, 'user2': 5.0, 'user3': 4.0, 'user4': 1.0} } return items
-
计算物品间的相似度矩阵
item_data = loadData() similarity_matrix = pd.DataFrame( np.identity(len(item_data)), index=item_data.keys(), columns=item_data.keys(), ) # 遍历每条物品-用户评分数据 for i1, users1 in item_data.items(): for i2, users2 in item_data.items(): if i1 == i2: continue vec1, vec2 = [], [] for user, rating1 in users1.items(): rating2 = users2.get(user, -1) if rating2 == -1: continue vec1.append(rating1) vec2.append(rating2) similarity_matrix[i1][i2] = np.corrcoef(vec1, vec2)[0][1] print(similarity_matrix)
A B C D E A 1.000000 -0.476731 -0.123091 0.532181 0.969458 B -0.476731 1.000000 0.645497 -0.310087 -0.478091 C -0.123091 0.645497 1.000000 -0.720577 -0.427618 D 0.532181 -0.310087 -0.720577 1.000000 0.581675 E 0.969458 -0.478091 -0.427618 0.581675 1.000000 -
从 Alice 购买过的物品中,选出与物品
E最相似的num件物品。target_user = ' Alice ' target_item = 'E' num = 2 sim_items = [] sim_items_list = similarity_matrix[target_item].sort_values(ascending=False).index.tolist() for item in sim_items_list: # 如果target_user对物品item评分过 if target_user in item_data[item]: sim_items.append(item) if len(sim_items) == num: break print(f'与物品{target_item}最相似的{num}个物品为:{sim_items}')
与物品E最相似的2个物品为:['A', 'D'] -
预测用户 Alice 对物品
E的评分target_user_mean_rating = np.mean(list(item_data[target_item].values())) weighted_scores = 0. corr_values_sum = 0. target_item = 'E' for item in sim_items: corr_value = similarity_matrix[target_item][item] user_mean_rating = np.mean(list(item_data[item].values())) weighted_scores += corr_value * (item_data[item][target_user] - user_mean_rating) corr_values_sum += corr_value target_item_pred = target_user_mean_rating + weighted_scores / corr_values_sum print(f'用户{target_user}对物品{target_item}的预测评分为:{target_item_pred}')
用户 Alice 对物品E的预测评分为:4.6
-
base 公式 $$ w_{i j}=\frac{|N(i) \bigcap N(j)|}{|N(i)|} $$
- 该公式表示同时喜好物品
$i$ 和物品$j$ 的用户数,占喜爱物品$i$ 的比例。 - 缺点:若物品
$j$ 为热门物品,那么它与任何物品的相似度都很高。
- 该公式表示同时喜好物品
-
对热门物品进行惩罚 $$ w_{i j}=\frac{|N(i) \cap N(j)|}{\sqrt{|N(i)||N(j)|}} $$
- 根据 base 公式在的问题,对物品
$j$ 进行打压。打压的出发点很简单,就是在分母再除以一个物品$j$ 被购买的数量。 - 此时,若物品
$j$ 为热门物品,那么对应的$N(j)$ 也会很大,受到的惩罚更多。
- 根据 base 公式在的问题,对物品
-
控制对热门物品的惩罚力度 $$ w_{i j}=\frac{|N(i) \cap N(j)|}{|N(i)|^{1-\alpha}|N(j)|^{\alpha}} $$
- 除了第二点提到的办法,在计算物品之间相似度时可以对热门物品进行惩罚外。
- 可以在此基础上,进一步引入参数
$\alpha$ ,这样可以通过控制参数$\alpha$ 来决定对热门物品的惩罚力度。
-
对活跃用户的惩罚
- 在计算物品之间的相似度时,可以进一步将用户的活跃度考虑进来。 $$ w_{i j}=\frac{\sum_{\operatorname{\text {u}\in N(i) \cap N(j)}} \frac{1}{\log 1+|N(u)|}}{|N(i)|^{1-\alpha}|N(j)|^{\alpha}} $$
- 对于异常活跃的用户,在计算物品之间的相似度时,他的贡献应该小于非活跃用户。
协同过滤算法存在的问题之一就是泛化能力弱:
- 即协同过滤无法将两个物品相似的信息推广到其他物品的相似性上。
- 导致的问题是热门物品具有很强的头部效应, 容易跟大量物品产生相似, 而尾部物品由于特征向量稀疏, 导致很少被推荐。
比如下面这个例子:
- 左边矩阵中,$A, B, C, D$ 表示的是物品。
- 可以看出,$D $ 是一件热门物品,其与
$A、B、C$ 的相似度比较大。因此,推荐系统更可能将$D$ 推荐给用过$A、B、C$ 的用户。 - 但是,推荐系统无法找出
$A,B,C$ 之间相似性的原因是交互数据太稀疏, 缺乏相似性计算的直接数据。
所以这就是协同过滤的天然缺陷:推荐系统头部效应明显, 处理稀疏向量的能力弱。
为了解决这个问题, 同时增加模型的泛化能力。2006年,矩阵分解技术(Matrix Factorization, MF)被提出:
- 该方法在协同过滤共现矩阵的基础上, 使用更稠密的隐向量表示用户和物品, 挖掘用户和物品的隐含兴趣和隐含特征。
- 在一定程度上弥补协同过滤模型处理稀疏矩阵能力不足的问题。
- 什么时候使用UserCF,什么时候使用ItemCF?为什么?
(1)UserCF
由于是基于用户相似度进行推荐, 所以具备更强的社交特性, 这样的特点非常适于用户少, 物品多, 时效性较强的场合。
- 比如新闻推荐场景, 因为新闻本身兴趣点分散, 相比用户对不同新闻的兴趣偏好, 新闻的及时性,热点性往往更加重要, 所以正好适用于发现热点,跟踪热点的趋势。
- 另外还具有推荐新信息的能力, 更有可能发现惊喜, 因为看的是人与人的相似性, 推出来的结果可能更有惊喜,可以发现用户潜在但自己尚未察觉的兴趣爱好。
(2)ItemCF
- 这个更适用于兴趣变化较为稳定的应用, 更接近于个性化的推荐, 适合物品少,用户多,用户兴趣固定持久, 物品更新速度不是太快的场合。
- 比如推荐艺术品, 音乐, 电影。
2.协同过滤在计算上有什么缺点?有什么比较好的思路可以解决(缓解)?
该问题答案参考上一小节的协同过滤算法的问题分析。
3.上面介绍的相似度计算方法有什么优劣之处?
cosine相似度计算简单方便,一般较为常用。但是,当用户的评分数据存在 bias 时,效果往往不那么好。
- 简而言之,就是不同用户评分的偏向不同。部分用户可能乐于给予好评,而部分用户习惯给予差评或者乱评分。
- 这个时候,根据cosine 相似度计算出来的推荐结果效果会打折扣。
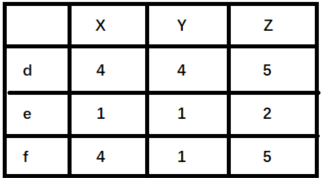
举例来说明,如下图(
X,Y,Z表示物品,d,e,f表示用户):
- 如果使用余弦相似度进行计算,用户 d 和 e 之间较为相似。但是实际上,用户 d 和 f 之间应该更加相似。只不过由于 d 倾向于打高分,e 倾向于打低分导致二者之间的余弦相似度更高。
- 这种情况下,可以考虑使用皮尔逊相关系数计算用户之间的相似性关系。
4.协同过滤还存在其他什么缺陷?有什么比较好的思路可以解决(缓解)?
- 协同过滤的优点就是没有使用更多的用户或者物品属性信息,仅利用用户和物品之间的交互信息就能完成推荐,该算法简单高效。
- 但这也是协同过滤算法的一个弊端。由于未使用更丰富的用户和物品特征信息,这也导致协同过滤算法的模型表达能力有限。
- 对于该问题,逻辑回归模型(LR)可以更好地在推荐模型中引入更多特征信息,提高模型的表达能力。