函数原型:
template< class InputIt, class T >
T accumulate( InputIt first, InputIt last, T init );一般求和的,代码如下:
int sum = accumulate(vec.begin() , vec.end() , 0);
int lower_bound(起始地址,结束地址,要查找的数值) 返回的是数值 第一个等于某元素 的位置。
int index = upper_bound(vec.begin(), vec.end(), target) - vec.begin()
功能:函数lower_bound()在first和last中的前闭后开区间进行二分查找,返回大于或等于target的第一个元素位置。如果所有元素都小于target,则返回last的位置,因为是前闭后开因此这个时候的last会越界,要注意。
找不到返回nums.end()
int upper_bound(起始地址,结束地址,要查找的数值) 返回的是数值 第一个大于某个元素 的位置。
int index = upper_bound(vec.begin(), vec.end(), target) - vec.begin();
功能:函数upper_bound()返回的在前闭后开区间查找的关键字的上界,返回大于target的第一个元素位置。注意:返回查找元素的最后一个可安插位置,也就是“元素值>查找值”的第一个元素的位置。同样,如果target大于数组中全部元素,返回的是last。(注意:数组下标越界)
bool binary_search(起始地址,结束地址,要查找的数值) 返回的是 是否存在 这么一个数,是一个bool值。
功能: 在数组中以二分法检索的方式查找,若在数组(要求数组元素非递减)中查找到indx元素则真,若查找不到则返回值为假。
template<
class T,
class Container = std::vector<T>,
class Compare = std::less<typename Container::value_type>
> class priority_queue;默认container是vector。
默认compare策略是less。因为默认是大顶堆,首先输出最大元素,所以最开始来的元素最后才输出。记住大顶堆比较策略是std::less<T>,小顶堆的比较策略是std::greater<T>
int atoi( const char *str );
将char*的字符串转化成整数
包含在c++标准库中头文件<algorithm>中
std::min(const T& a, const T& b);
std::max(const T& a, const T& b);
//或者自己写comp函数
const T& min (const T& a, const T& b, Compare comp);
//自定义compare函数如下
static bool compare(const string& s1, const string& s2)
{
string ab = s1 + s2;
string ba = s2 + s1;
return ab < ba; //升序排列。如改为ab > ba, 则为降序排列
}
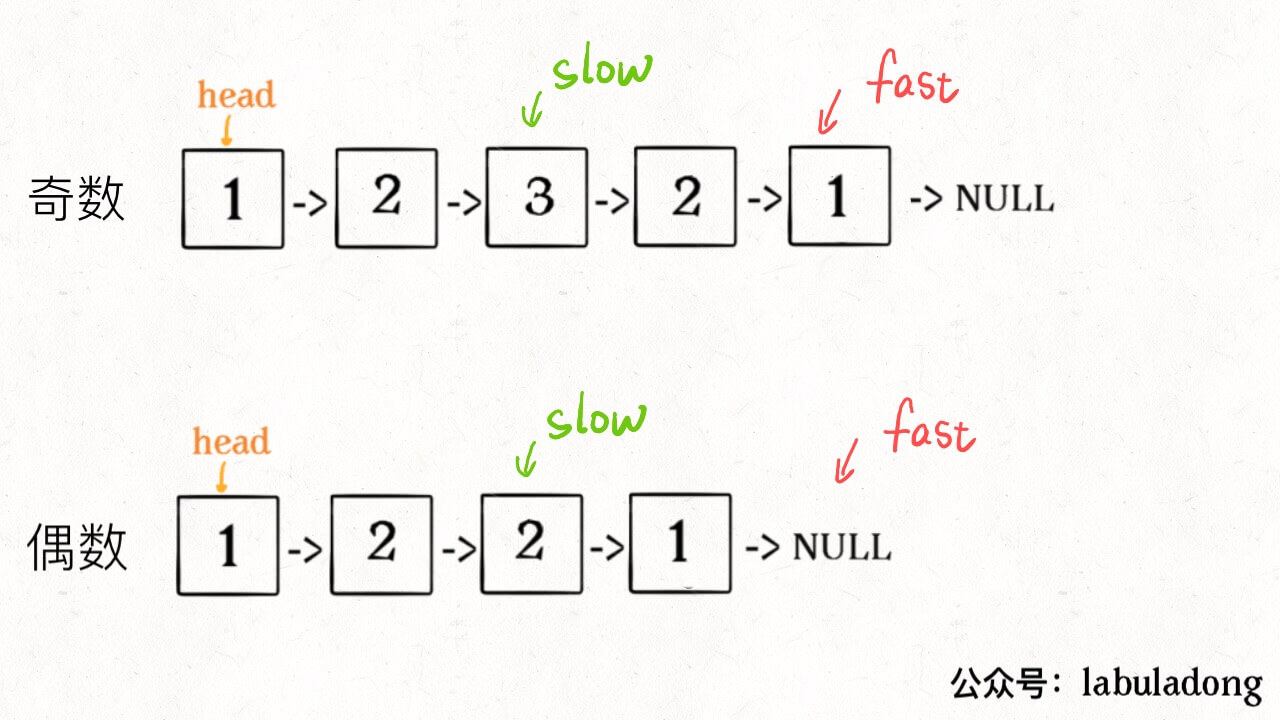
**思路:**回文串是对称的,所以正着读和倒着读应该是一样的,这一特点是解决回文串问题的关键。单链表无法倒着遍历,无法使用双指针技巧。
-
方法一,把链表节点放入栈中再拿出和原来的链表比较。算法的时间和空间复杂度都是 O(N)
class Solution { public: bool isPalindrome(ListNode* head) { stack<int> rec; ListNode *temp = head; while(temp){ rec.push(temp->val); temp = temp->next; } while(!rec.empty()||head){ if(head->val == rec.top()){ head = head->next; rec.pop(); }else{ return false; } } return true; } };
-
方法二
**利用双指针的快慢指针的思想,找出链表的中间节点。**双指针的条件是while(fast!=null && fast->next!=null)
然后要分清楚链表是双数还是单数。如果fast==null,表明是偶数链表,否则是奇数链表
双指针找中点+反转一部分节点
bool isPalindrome(ListNode* head) {
ListNode* slow = head;
ListNode* fast = head;
while(fast && fast->next){
slow = slow->next;
fast = fast->next->next;
}
//fast=nullptr说明是偶数链表
//fast!=nullptr说明是奇数链表
ListNode* tail = reverse(slow);
ListNode* front = head;
while(tail || tail == slow){
if(front->val == tail->val){
front = front->next;
tail = tail->next;
}else{
return false;
}
}
return true;
}
ListNode* reverse(ListNode* node){
if(!node || !node->next){
return node;
}
ListNode* tmp = reverse(node->next);
node->next->next = node;
node->next = nullptr;
return tmp;
}本质上是走过自己的路,再走过对方的路,这是求两个链表相交的方法
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
//本质上是走过自己的路,再走过对方的路
if(headA == NULL|| headB == NULL){
return NULL;
}
ListNode* temp_a = headA;
ListNode* temp_b = headB;
while(temp_a!=temp_b){
if(temp_a == NULL){
temp_a = headB;
}else{
temp_a = temp_a->next;
}
if(temp_b == NULL){
temp_b = headA;
}else{
temp_b = temp_b->next;
}
}
return temp_a;
}双指针法
情况一:两个链表相交。这个好判断
情况二:两个链表不相交。由于两个链表没有公共节点,两个指针也不会同时到达两个链表的尾节点,因此两个指针都会遍历完两个链表,指针pA 移动了m+n 次、指针pB 移动了 n+m 次之后,两个指针会同时变成空值null,此时返回null,满足循环条件。
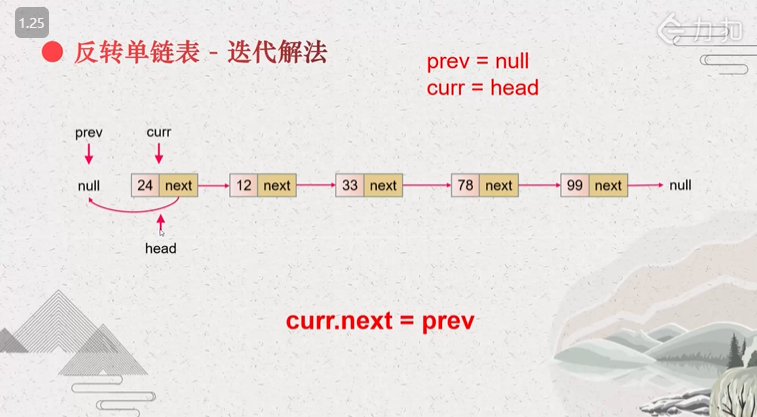
ListNode* reverseList(ListNode* head) {
if(head == nullptr){
return head;
}
if(head->next == nullptr){
return head;
}
ListNode *temp = reverseList(head->next);
head->next->next = head;
head->next = nullptr;
return temp;
}上面这段代码是反转列表标准递归代码,也很好理解
使用迭代好理解。这道题第一反应就是四种种情况,全是空,一个是空,全不为空。
正常理解就是if,else if什么的,但是这样在写全不为空的时候很麻烦。
下面代码一个while(l1 && l2)就解决了上面的问题,很巧妙,很值得记住。必须全不为空才能进入循环,有一个是空指针就不能进入,这样代码好写很多很多
ListNode *head = new ListNode(-1);
ListNode *pre = head;
while(l1 && l2){
ListNode* temp1 = l1;
ListNode* temp2 = l2;
if(l1->val >= l2->val){
pre->next = l2;
l2 = l2->next;
}else{
pre->next =l1;
l1 = l1->next;
}
pre = pre->next;
}
if(l1 == nullptr){
pre->next = l2;
}
if(l2 ==nullptr){
pre->next = l1;
}
return head->next;
}思路:用快慢指针,如果是环形链表会相交
主要点在于while的循环条件,一定要针对快指针进行条件判断同时用&&而不是||
bool hasCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
if(head == nullptr || head->next == nullptr){
return false;
}
while(fast != nullptr && fast->next != nullptr){
slow = slow->next;
fast = fast->next->next;
if(fast == slow){
return true;
}
}
return false;
}这道题自己画图就知道了,本质就是一道数学题。
ListNode *detectCycle(ListNode *head) {
ListNode* slow = head;
ListNode* fast = head;
while(fast && fast->next){
slow = slow->next;
fast = fast->next->next;
if(slow == fast){
fast = head;
while(fast != slow){
fast = fast->next;
slow = slow->next;
}
return fast;
}
}
return nullptr;
}当碰到链表第几个节点的时候,双指针的思想可能正合适。
我们可以设想假设设定了双指针 p 和 q 的话,当 q 指向末尾的 NULL,p 与 q 之间相隔的元素个数为 n 时,那么删除掉 p 的下一个指针就完成了要求。

ListNode* removeNthFromEnd(ListNode* head, int n) {
//双指针思想,以后这种倒数的长度类型的题目都可以用双指针
ListNode* p = head;
ListNode* q = head;
while(n>0){
p = p->next;
n--;
}
if(!p){
return head->next;
}
while(p->next){
p = p->next;
q = q->next;
}
q->next = q->next->next;
return head;
}思路:交换节点的题,就要有temp->next和temp->next->next。
如果 temp 的后面没有节点或者只有一个节点,则没有更多的节点需要交换,因此结束交换。否则,获得 temp 后面的两个节点 node1(temp->next)和 node2(temp->next->next),通过更新节点的指针关系实现两两交换节点。
下面是错误代码
ListNode* swapPairs(ListNode* head) {
ListNode* temp = new ListNode(-1);
temp->next = head;
while(temp->next&&temp->next->next){
ListNode* l1 = temp->next;
ListNode* l2 = temp->next->next;
temp->next = l2;
l1->next =l2->next;
l2->next = l1;
temp = l1;
}
return head;
}输入:1,2,3,4
输出:1,4,3
错误原因:注意这道题head节点指的是首节点!这是最重要一点。其次,最开始head节点为1,在上面代码交换结束后正常来说为2,1,4,3,但是,head节点此刻还是1,如果返回head,则2被漏掉
正确代码
ListNode* swapPairs(ListNode* head) {
ListNode* temp = new ListNode(-1);
temp->next = head;
ListNode* dummy = temp;
while(temp->next&&temp->next->next){
ListNode* l1 = temp->next;
ListNode* l2 = temp->next->next;
temp->next = l2;
l1->next =l2->next;
l2->next = l1;
temp = l1;
}
return dummy->next;
}思路:直接加,注意进位条件不要用if,核心代码在于
sum = l1->val + l2->val + carry;
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* dummy = new ListNode();
ListNode* dummy_head = dummy;
int carry = 0;
int sum = 0;
int single = 0;
while(l1 && l2){
sum = l1->val + l2->val + carry;
carry = sum / 10;
single = sum % 10;
ListNode* node = new ListNode(single);
dummy -> next = node;
dummy = dummy->next;
l1 = l1->next;
l2 = l2->next;
}
while(l1){
sum = l1->val + carry;
carry = sum / 10;
single = sum % 10;
ListNode* node = new ListNode(single);
dummy -> next = node;
dummy = dummy->next;
l1 = l1->next;
}
while(l2){
sum = l2->val + carry;
carry = sum / 10;
single = sum % 10;
ListNode* node = new ListNode(single);
dummy -> next = node;
dummy = dummy->next;
l2 = l2->next;
}
if(carry){
ListNode* node = new ListNode(carry);
dummy -> next = node;
dummy = dummy->next;
}
return dummy_head->next;
}思路:用栈,这样如果两个链表长度不相等的时候不用那么麻烦。
难点在于代码的细节控制。
- 当代码中出现空栈时候,则对应的数置为0,不要再写if判断了。
- 用第三个栈重建一个链表,这样耗费空间。可以参考第一种写法,总之这道题在于细节控制,思想上不难。
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
stack<int> s1;
stack<int> s2;
int carry = 0;
int sum = 0;
int single = 0;
ListNode* dummy = new ListNode();
ListNode* dummy_head = dummy;
while(l1){
s1.push(l1->val);
l1=l1->next;
}
while(l2){
s2.push(l2->val);
l2 = l2->next;
}
while(!s1.empty() && !s2.empty()){
sum = s1.top() + s2.top() + carry;
single = sum % 10;
carry = sum / 10;
ListNode * tmp = new ListNode(single);
dummy -> next = tmp;
dummy = dummy->next;
s1.pop();
s2.pop();
}
while(!s1.empty()){
sum = s1.top() + carry;
single = sum % 10;
carry = sum / 10;
ListNode * tmp = new ListNode(single);
dummy -> next = tmp;
dummy = dummy->next;
s1.pop();
}
while(!s2.empty()){
sum = s2.top() + carry;
single = sum % 10;
carry = sum / 10;
ListNode * tmp = new ListNode(single);
dummy -> next = tmp;
dummy = dummy->next;
s2.pop();
}
if(carry){
ListNode * tmp = new ListNode(carry);
dummy -> next = tmp;
dummy = dummy->next;
}
ListNode* reverse_head = reverse(dummy_head->next);
return reverse_head;
}
ListNode* reverse(ListNode* node){
if(!node || !node->next){
return node;
}
ListNode* tmp = reverse(node->next);
node->next->next = node;
node->next = nullptr;
return tmp;
}思路:这道题就是先求出链表长度,然后分段。
主要难点在于断链,vector每一个索引都是一个链表,在锻炼表操作这里我足足困了好长时间
其实重点就两句话:dummy = root; root = root->next;(这个代码是设置前置节点的最好办法)
因为我们要找到前置节点,其实很简单
dummy = root中dummy就可以变成前置节点了!!!
vector<ListNode*> splitListToParts(ListNode* root, int k) {
//计算长度
int length = 0;
ListNode* temp = root;
while(temp){
length++;
temp = temp->next;
}
//每个断链的长度
int arry_len = (length / k) > 0 ? (length / k) : 1;
int arry[k];
for(int i = 0;i < k; i++){
arry[i] = arry_len;
}
//因为长度差不超过一,因此根据length和k*arry_len的差依次给前面的每个值+1
int gap = 0;
if((k * arry_len) < length){
gap = length - (k * arry_len);
for(int i = 0;i < gap;i++){
arry[i]++;
}
}
//断链表操作
vector<ListNode*> splict;
ListNode* dummy ;
for(int i = 0; i < k; i++){
splict.push_back(root);
for(int j = 0;j < arry[i];j++){
if(root){
dummy = root;/*前置结点的精髓所在*/
root = root->next;
}
}
if(dummy){
dummy->next = NULL;
}
}
return splict;
}双指针然后拼接
ListNode* oddEvenList(ListNode* head) {
if(!head || !head->next || !head->next->next){
return head;
}
ListNode* odd = head;
ListNode* even = head->next;
ListNode* dummy = even;
while(odd->next && even->next){
odd->next = even->next;
odd = odd->next;
even->next = odd->next;
even = even->next;
}
odd->next = dummy;
return head;
}反转链表精髓:
关于反转链表相关的递归思想,看这个
这个反转链表,思想和反转前n个链表一模一样。
只不过,第一个left不是从1开始反转,那又如何?我们可以让他变成从1开始,想一想。
反转前n个链表
ListNode* temp = nullptr;
ListNode* reverseN(int n,ListNode* node){
if(n == 1){
temp = node->next;
return node;
}
ListNode* last = reverseN(n-1, node->next);
node->next->next = node;
node->next = temp;
return last;
}这道题解,递归解法----反转链表递归解法还是比较简单的
ListNode* reverseBetween(ListNode* head, int left, int right) {
ListNode* dummy = head;
ListNode* n1 = nullptr;
int length = right - left +1;
while(left > 1){
n1 = dummy;/*记录前一个节点*/
dummy = dummy->next;
left--;
}
ListNode* n2 = reverseN(length, dummy);
//n1为空说明left就是1,从第一个位置反转的!!!
if(n1){
n1->next = n2;
}else{
return n2;
}
return head;
}
ListNode* temp = nullptr;
ListNode* reverseN(int n,ListNode* node){
if(n == 1){
temp = node->next;
return node;
}
ListNode* last = reverseN(n-1, node->next);
node->next->next = node;
node->next = temp;
return last;
}
/*******************第二种解法***********************/
/*有两个dummy节点,begin前和end后,因此要判断四次*/
ListNode* reverseBetween(ListNode* head, int left, int right) {
if(!head || !head->next){
return head;
}
ListNode* begin = head;
ListNode* end = head;
ListNode* dummy = nullptr;
while(left > 1){
dummy = begin;
begin = begin->next;
left--;
}
while(right > 1){
end = end->next;
right--;
}
ListNode* dummy2 = end->next;
ListNode* node = reverse(begin, end);
if(!dummy && !dummy2){
cout<<"1"<<endl;
return end;
}
else if(!dummy && dummy2){
cout<<"2"<<endl;
begin->next = dummy2;
return end;
}
else if(dummy && !dummy2){
cout<<"3"<<endl;
dummy->next = end;
return head;
}
cout<<"4"<<endl;
dummy->next = node;
begin->next = dummy2;
return head;
}
ListNode* reverse(ListNode* begin, ListNode* end){
if(begin == end){
return begin;
}
ListNode* tmp = reverse(begin->next, end);
begin->next->next = begin;
begin->next = nullptr;
return tmp;
}思路如图所示,很好理解。
ListNode* deleteDuplicates(ListNode* head) {
if(!head || !head->next){
return head;
}
int value = head->val;
ListNode* temp = head->next;
ListNode* carry = head;
while(temp){
if(temp->val == value){
ListNode* dummy = temp;
temp = temp->next;
carry->next = temp;
delete dummy;
dummy = nullptr;
}else{
carry = carry->next;
value = carry->val;
temp = temp->next;
}
}
return head;
}这道题本质上还是用的反转前n个链表的思想。
具体细节如下:
先调用一次函数,使用一个newHead接受返回值,这个是为了方便最后函数的返回。
调用reverseN这个函数的时候,要标记反转这段链表的前置节点和后置节点。后面会用到。
反转后的这部分区间的链表,node接受前置节点,tail接受后置接点。
记住,前一个区间的tail节点就是区间中的最后一个节点,这个节点要放到tail_temp中,然后调用reverseN后,会得到新的tail节点,让tail_temp->next指向tail节点,这样两个区间就会接上。
ListNode* dummy = nullptr;
ListNode* tail = nullptr;
ListNode* reverseKGroup(ListNode* head, int k) {
int length = 0;
ListNode* temp = head;
if(k == 1){
return head;
}
/*计算链表长度*/
while(temp){
temp = temp->next;
length++;
}
//减一是因为第一次的时候,要确定head指针
int loop = length / k - 1;
ListNode* newHead = reverseN(k, head);
head = dummy;
for(int i = 0;i < loop;i++){
head = dummy;
ListNode* tail_temp = tail;
ListNode* node = reverseN(k, head);
tail_temp->next = node;
}
return newHead;
}
ListNode* reverseN(int n, ListNode* head){
if(n == 1){
dummy = head->next;
return head;
}
ListNode* last = reverseN(n-1, head->next);
head->next->next = head;
head->next = dummy;
tail = head;
return last;
}-
递归的做法
其实做了这么多次回头再来看这道题发现一个问题,即链表的本质是改变连接方向就行,而在改变连接方向的时候一定要断开之前的链子,即
node->next=nullvector<int> reversePrint(ListNode* head) { vector<int> res; ListNode* newHead = reverse(head); while(newHead){ res.push_back(newHead->val); newHead = newHead->next; } return res; } ListNode* reverse(ListNode* head){ if(!head || !head->next){ return head; } ListNode* tmp = reverse(head->next); head->next->next = head; head->next = nullptr; return tmp; }
-
双指针递归的做法
这也不失为一种思路
-
用一个辅助栈就行
-
c++的reverse函数,放到数组里面直接反转
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head || !head->next){
return head;
}
ListNode* tmp = reverseList(head->next);
head->next->next = head;
head->next = nullptr;
return tmp;
}
};-
暴力复制法
先复制俩表的next节点,然后依次寻找每个节点的random指针,时间复杂度$O(n^2)$
-
辅助空间
整个hash表,记录一下random指针的位置,然后复制的时候填进去就行,空间复杂度$O(n)$
-
终极牛逼法
时间复杂度$O(n)$
第三步就是拆分
**关键点,不能改原链表,你加完重复链表之后需要复原,!!!**不然会报Next pointer of node with label 7 from the original list was modified.这种错误,表示修改了原链表
class Solution { public: Node* copyRandomList(Node* head) { if(!head){ return head; } Node* new_head = nullptr; new_head = head; //重复每个链表节点 while(new_head){ Node* tmp = new Node(new_head->val); tmp->next = new_head->next; new_head->next = tmp; new_head = new_head->next->next; } new_head = head; //重定义random指针 while(new_head){ if(new_head->random != nullptr){ new_head->next->random = new_head->random->next; } new_head = new_head->next->next; } //把处于偶数的链表拿出来 Node* copy_head = head->next; Node* copy_head_return = head->next; new_head = head; while(copy_head->next){ new_head->next = new_head->next->next; new_head = new_head->next; copy_head->next = new_head->next; copy_head = copy_head->next; } new_head->next = nullptr; return copy_head_return; } };
++++
个人对递归的一些感悟。
递归的原理非常简单,就是函数出栈入栈。
但很多时候我们都会被递归绕晕,原因就是我们想的太复杂了。做题的时候,一定要先明确函数的定义是什么,然后根据定义来写递归语句。记住,千万不要跳入递归的细节,有时候不考虑细节反而容易实现,考虑细节的话可能会绕进去!
写树相关的算法,简单说就是,先搞清楚当前
root节点「该做什么」以及「什么时候做」,然后根据函数定义递归调用子节点把递归的问题放眼到三个节点中,即根节点,右节点左节点。
重中之重!!!!!!!
递归函数什么时候有返回值什么时候没有返回值,比如有 root->left = invertTree(root->left);这种和return searchBST(root->left,val);这两种代码到底有何区别的?
答:有以下三点:
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。(这种情况就是本文下半部分介绍的113.路径总和ii)
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。 (这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍)
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。(本题的情况)
只要把二叉树上的每一个节点的左右子节点进行交换,最后的结果就是完全翻转之后的二叉树。
只能用后序和前序,不能用中序。因为需要交换左右子节点,必须先知道左右子节点。如果用中序的话只知道左节点和根节点,不知道右节点,无法反转。
注意节点交换细节,和普通变量一样
TreeNode* invertTree(TreeNode* root) {
if(!root){
return NULL;
}
TreeNode* temp = root->left;
root->left = root->right;
root->right = temp;
root->left = invertTree(root->left);
root->right = invertTree(root->right);
return root;
}bool hasPathSum(TreeNode* root, int sum) {
if(!root){
return false;
}
sum -= root->val;
if(!root->left && !root->right){
return sum == 0;
}
return hasPathSum(root->left, sum) || hasPathSum(root->right, sum);
}vector<vector<int>> res;
vector<int> tmp;
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
recurse(root, targetSum);
return res;
}
void recurse(TreeNode* root, int targetSum){
if(!root){
return;
}
tmp.push_back(root->val);
targetSum -= root->val;
if(!root->left && !root->right && targetSum == 0){
res.emplace_back(tmp);
}
recurse(root->left, targetSum);
recurse(root->right, targetSum);
tmp.pop_back();
}还是老样子,关注局部的三个节点,根左右,然后写出代码。
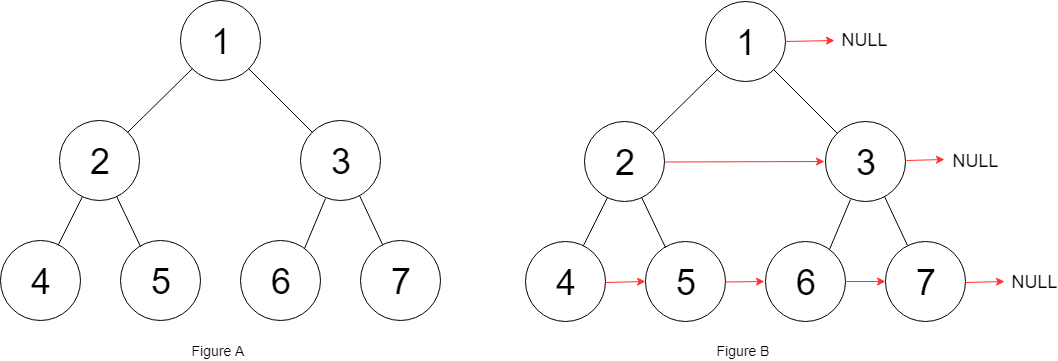
关键点不是2->3这种一个根节点下的节点,而是5->6这种不在同一个根节点下的。因此要借助5和6的上层节点2,3来解决问题。通过2到3,再到6,就可以链接5和6
Node* connect(Node* root) {
if(!root){
return NULL;
}
if(root->left){
root->left->next = root->right;
if(root->next && root->right){
root->right->next = root->next->left;
}
}
connect(root->left);
connect(root->right);
return root;
}关键点:先递归右子树
画一下就知道了,画一个四层的二叉树,然后右子树多画几个节点就知道为啥了
Node* connect(Node* root) {
if(!root || (!root->left && !root->right)){
return root;
}
if(root->left && root->right){
root->left->next = root->right;
root->right->next = get_next_node(root);
}
if(!root->right){
cout<<"1"<<endl;
root->left->next = get_next_node(root);
}
if(!root->left){
root->right->next = get_next_node(root);
}
connect(root->right);
connect(root->left);
return root;
}
Node* get_next_node(Node* root){
while(root->next){
if(root->next->left){
return root->next->left;
}
else if(root->next->right){
return root->next->right;
}
root = root->next;
}
return nullptr;
}将左子树上的东西都放到右子树上去,递归的写,注意,只关注局部即可。
void flatten(TreeNode* root) {
if(!root ){
return ;
}
flatten(root->left);
flatten(root->right);
//最后处理根节点
TreeNode* tmp_right = root->right;
root->right = root->left;
root->left = nullptr;
TreeNode* tmp = root;
while(tmp->right){
tmp = tmp->right;
}
tmp->right = tmp_right;
}TreeNode constructMaximumBinaryTree([3,2,1,6,0,5]) { // 找到数组中的最大值 TreeNode root = new TreeNode(6); // 递归调用构造左右子树 root.left = constructMaximumBinaryTree([3,2,1]); root.right = constructMaximumBinaryTree([0,5]); return root;}上面代码就是本体的答题思路。
对于构造二叉树的问题,根节点要做的就是把想办法把自己构造出来。
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
int left = 0;
int right = nums.size();
return build_binary_tree(nums, left, right);
}
TreeNode* build_binary_tree(vector<int>& nums, int left, int right){
//递归结束条件
if(left >= right){
return nullptr;
}
int max = INT_MIN;
int index = -1;
for(int i = left;i < right;i++){
if(max < nums[i]){
max = nums[i];
index = i;
}
}
TreeNode* root = new TreeNode(max);
root->left = build_binary_tree(nums, left, index);
root->right = build_binary_tree(nums, index + 1, right);
return root;
}⭕105. 从前序与中序遍历序列构造二叉树(★面试常考)
代码思路还是跟654题一模一样,可以说,构造二叉树的题递归代码都差不多!
这道题的思路用一下图片即可说明:
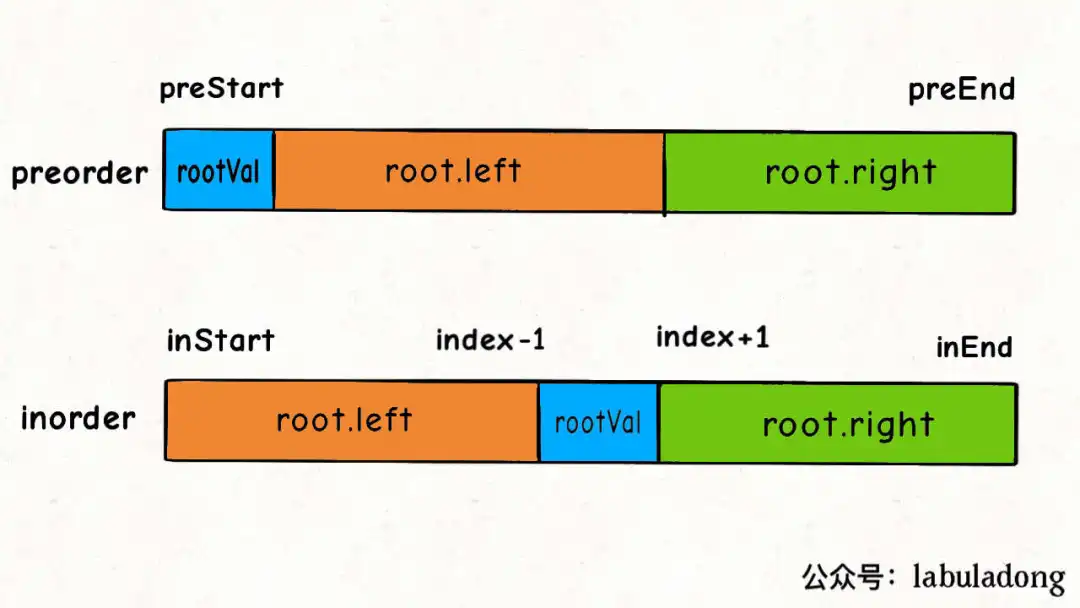
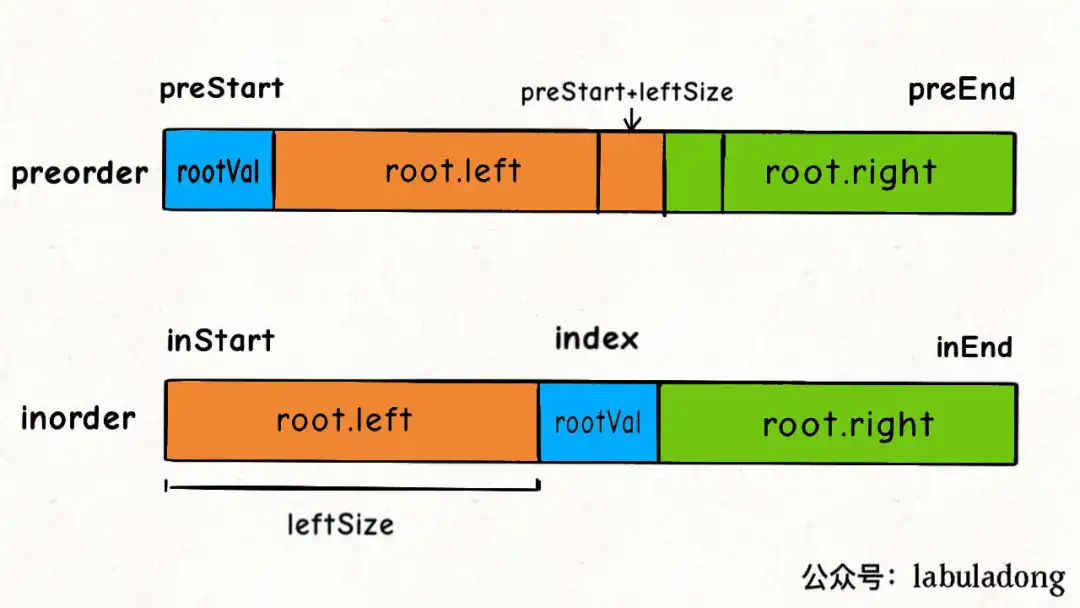
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(preorder.size() == 0){
return nullptr;
}
return build_tree_instance(preorder, 0, preorder.size(),
inorder, 0, inorder.size());
}
TreeNode* build_tree_instance(vector<int>& preorder, int pre_left, int pre_right,
vector<int>& inorder, int in_left, int in_right){
if(in_left >= in_right){
return nullptr;
}
int left_count = 0;
int index = -1;
int root_value = preorder[pre_left];
for(int i = in_left;i < in_right; i++){
if(root_value == inorder[i]){
index = i;
break;
}
}
left_count = index - in_left;
TreeNode* root = new TreeNode(root_value);
root->left = build_tree_instance(preorder,pre_left+1, pre_left+left_count,
inorder, in_left, index);
root->right = build_tree_instance(preorder,pre_left+left_count+1, pre_right,
inorder, index+1, in_right);
return root;
}跟上一题思路一模一样
但是这道题第一次做困了很久,就是边界找不准,一直有问题,一定要好好想想。
主要是前序和后序数组的边界不好找,中序的两道题都一样。
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(inorder.size() == 0){
return nullptr;
}
return bulid_tree_instance(inorder, 0, inorder.size(),
postorder, 0, postorder.size());
}
TreeNode* bulid_tree_instance(vector<int>& inorder, int in_left, int in_right,
vector<int>& postorder, int post_left, int post_right){
if(in_left >= in_right){
return nullptr;
}
int index = 0;
int left_count = 0;
int root_val = postorder[post_right-1];
for(int i = in_left;i < in_right; i++){
if(root_val == inorder[i]){
index = i;
break;
}
}
left_count = index - in_left;
TreeNode* root = new TreeNode(root_val);
root->left = bulid_tree_instance(inorder,in_left, index,
postorder,post_left, post_left+left_count);
root->right = bulid_tree_instance(inorder, index+1, in_right,
postorder, post_left+left_count, post_right-1); //post_right -1 这个是最容易被忽视的,后序遍历要看最后一个值
return root;
}这道题的思想还是一个:对于树的某一个节点,清楚他要干啥!
所以这道题有两步:①以我自己为根的子树长什么样子。 ②以其他节点为根的子树的样子
以某一个节点为根的子树的样子,很明显就是后序遍历
接着序列化原先的二叉树,对比一下就行
map<string,int> map_tree;
vector<TreeNode*> vec_tree;
vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
sqe_tree(root);
return vec_tree;
}
string sqe_tree(TreeNode* root){
if(!root){
return "#";
}
string left = sqe_tree(root->left);
string right = sqe_tree(root->right);
string str_tree = left + "," + right + "," + to_string(root->val);
if(map_tree[str_tree] == 1){
vec_tree.push_back(root);
}
//重要
map_tree[str_tree]++;
return str_tree;
}这道题总结一下,有以下两个点。本题涉及的数据结构知识,本题的细节。
-
本题的细节
这道题耗费我较多时间。有几个需要注意的点。
- 二叉树序列化的方法,需要写一个辅助函数完成,辅助函数的返回值用string,这个需要好好记住。
- 最开始存储序列化后的字符串用的是set,但我发现一个巨大的问题。即如果有set中重复的被找到,则放到vector中,这本来没什么问题,但是,注意这里面有个坑,即只要重复就放到vector中。这是you逻辑问题的,因为如果一个字符串重复了5次,vector中应该只有一个根节点,但是代码会放4次相同的根节点,这样vector中会出现重复,这是会出错的。所以用map方便。
-
涉及的数据结构
stl的关联式容器中有两个大类:set和map。由这两个基本关联式容器衍生出来很多,例如multimap、multiset、unordered_map、unordered_set。
- set就是数学上所说的元素的集合,可以理解为键和值完全相等的关联式容器。set会根据各个元素值的大小进行生序排序,底层使用红黑树来实现。值不能重复,由insert保证。
- map是由键和值两部分组成的关联式容器。键必须唯一,因此如果遇到有相同键的情况,可以使用[]运算符让值++,比如
map[str]++。根据键map会进行生序排序。insert保证了键的唯一性。底层用红黑树实现。 - multiset。顾名思义,键(值)可以重复的关联式容器。底层用红黑树实现。
- multimap。键可以重复的关联式容器,其他与map都一样。
- unordered_set。底层是哈希表,占用空间较多,查找是常数时间。无自动排序功能。
- unordered_map。底层是哈希表,占用空间较多,查找是常数时间。无自动排序功能。
-
思路:本质上就是节点间信息的交流。那么二叉树有三种信息交流的方式,前序,中序和后序。
由于我们可以分析,返回最小的摄像头数量,那么我们肯定尽量不在子节点装摄像头,而是在父节点装。因此从子节点往父节点传递信息的方式是后序遍历,我们可以用后序遍历的形式做这道题。
很自然,每个节点肯定有三种该状态啦:
- 0表示没有被监控
- 1表示该节点有摄像头
- 2表示被监控到了
然后我们就按照后序遍历,依次传递消息。
本质上是贪心,因为如果子节点被覆盖了,那么当前父节点就不要设置监视器,这是一条隐形规则。
-
代码
class Solution { public: int result; int minCameraCover(TreeNode* root) { result = 0; if(bianli(root) == 0){ result++; } return result; } int bianli(TreeNode* root){ if(root == nullptr){ return 2; } int left = bianli(root->left); int right = bianli(root->right); //逻辑部分 // 0表示没有被监控 // 1表示该节点有摄像头 // 2表示被监控到了 //①左右节点都被监控了。因为是自下而上,已经被监控了,其父节点就不用摄像头了,父节点就是没被监控 if(left == 2 && right ==2){ return 0; } //②左右节点至少有一个没被监控。说明父节点要放摄像头 if(left == 0 || right == 0){ result++; return 1; } //③左右节点至少有一个摄像头,那么父节点会被监控到 if(left ==1 || right ==1){ return 2; } return -1; }
所有树的题目,都想成一颗只有根、左节点、右节点 的小树。然后一颗颗小树构成整棵大树,所以只需要考虑这颗小树即可。接下来分情况, 按照题意:一颗三个节点的小树的结果只可能有如下6种情况:
- 根 + 左 + 右
- 根 + 左
- 根 + 右
- 根
- 左
- 右
只有 2,3,4 可以向上累加,而1,5,6不可以累加(这个很好想,情况1向上累加的话,必然出现分叉,情况5和6直接就跟上面的树枝断开的,没法累加),所以我们找一个全局变量存储 1,5,6这三种不可累加的最大值, 另一方面咱们用遍历树的方法求2,3,4这三种可以累加的情况。 最后把两类情况得到的最大值再取一个最大值即可。
class Solution {
public:
int case1 = INT_MIN;
int maxPathSum(TreeNode* root) {
int case2 = dfs(root);
return max(case1, case2);
}
int dfs(TreeNode* root){
if(!root){
//注意,不能return0,-3这个例子就出粗哦了
//因为节点会比0更小
return -1000;
}
int left = dfs(root->left);
int right = dfs(root->right);
//一下三种情况无法回溯给父节点收益,所以只能全局变量Case1记录一下。
case1 = max(root->val + left + right, case1);
case1 = max(case1, left);
case1 = max(case1, right);
int case2 = root->val;
case2 = max(case2, root->val + left);
case2 = max(case2, root->val + right);
return case2;
}
};TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root || root == q || root == p){
return root;
}
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if(!left){
return right;
}
if(!right){
return left;
}
if(!left && !right){
return nullptr;
}
return root;
}思路:本质上还是层序遍历,只不过要循环一下每一层的节点数而已
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
queue<TreeNode* > m_queue;
if(root){
m_queue.push(root);
}
while(!m_queue.empty()){
int len = m_queue.size();
vector<int> rec;
for(int i = 0; i < len; i++){
TreeNode* tmp = m_queue.front();
rec.push_back(tmp->val);
m_queue.pop();
if(tmp->left){
m_queue.push(tmp->left);
}
if(tmp->right){
m_queue.push(tmp->right);
}
}
result.push_back(rec);
}
return result;
}
};这个题就是完全二叉树的性质,给一个二叉树,然后判断有几个节点,下图很能说明情况:
如果是满二叉树,直接就是$2^n-1$,如果不是满二叉树,那么就往下递归呗
int countNodes(TreeNode* root) {
if(!root){
return 0;
}
int left_height = 0;
int right_height = 0;
TreeNode* left_node = root->left;
TreeNode* right_node = root->right;
while(left_node){
left_node = left_node->left;
left_height++;
}
while(right_node){
right_node = right_node->right;
right_height++;
}
if(left_height == right_height){
return (2<<left_height) - 1;
}
return countNodes(root->left) + countNodes(root->right) + 1; //1是根节点
}TreeNode* searchBST(TreeNode* root, int val) {
if(!root){
return nullptr;
}
if(root->val == val){
return root;
}
else if(root->val < val){
return searchBST(root->right,val);
}
else if(root->val > val){
return searchBST(root->left,val);
}
return nullptr;
}-
知识点
递归返回函数名称有什么需要注意的?
-
数据结构
BST数增山查改由于本身性质的原因,和普通二叉树肯定不一样。
因此本身是有框架的,如下
void BST(TreeNode root, int target) { if (root.val == target) // 找到目标,做点什么 if (root.val < target) BST(root.right, target); if (root.val > target) BST(root.left, target); }
这题是BST(二叉搜索树)
思路一: BST中序遍历就是升序排序,因此可以用中序遍历做,但是时间复杂度是O(n),有点大,不太行
思路二:参考链接,题目中给定的数据结构无法实现思路二
vector<int> vec;
int kthSmallest(TreeNode* root, int k) {
reverse_tree(root);
return vec[k-1];
}
void reverse_tree(TreeNode* root){
if(!root){
return ;
}
reverse_tree(root->left);
vec.push_back(root->val);
reverse_tree(root->right);
return ;
}-
题目细节
由于原函数返回值是int,不适合递归,因此需要重新新一个辅助函数来完成树的递归。
-
涉及的数据结构
-
BST(二叉搜索树)是一个有序的基础树,avl、rb_tree是在其基础上而来的,是自平衡的树,提供logN级别的增山查改效率
-
BST树的特点:
- 对于 BST 的每一个节点
node,左子树节点的值都比node的值要小,右子树节点的值都比node的值大。 - 对于 BST 的每一个节点
node,左子树节点的值都比node的值要小,右子树节点的值都比node的值大。
- 对于 BST 的每一个节点
-
BST树中序遍历就是升序排序。
-
这道题真的真的特别的巧!!!!!
本质上还是二叉树的中序遍历,但是正常是升序。
我们需要逆序的节点顺序,因此先右后左不就行了!
int sum = 0;
TreeNode* convertBST(TreeNode* root) {
if(!root){
return nullptr;
}
convertBST(root->right);
root->val = sum + root->val;
sum = root->val;
convertBST(root->left);
}这道题就是巧!没别的!
思路一:中序遍历是升序,别忘了!
思路二:递归,每一个根节点左子树也是BST,右子树也是BST
思路二有坑,主要在于对于每一个节点root,我们可能会写成判断root节点的左节点小于和右节点大于。这是错误的,因为BST树保证了必须是左节点为根节点的数也是BST,右节点同理
思路一代码:
long long temp = (long long)INT_MIN-1;
bool isValidBST(TreeNode* root) {
if(!root){
return true;
}
if(!isValidBST(root->left)){
return false;
}
if(temp >= root->val){
return false;
}
temp = root->val;
if(!isValidBST(root->right)){
return false;
}
return true;
}
上述代码可能不好理解,换一种写法,
long long temp = (long long)INT_MIN-1;
bool isValidBST(TreeNode* root) {
if(!root){
return true;
}
bool left = isValidBST(root->left);
if(temp >= root->val){
return false;
}
temp = root->val;
bool right = isValidBST(root->right);
return left && right;
}-
本题需要注意的点
-
老生常谈的问题,在做递归的时候return不知道该怎么写。这道题函数的返回值是布尔类型,所以你也要写布尔类型的返回值,但是如何return就是一门学问了!
-
注意看代码
long long temp = (long long)INT_MIN-1;这样写是因为有一个测试用例,[-2147483648] 这个值就是INT_MIN所以,我们最小值必须使用比INT_MIN小的才行,所以int越界了,就用long long ,不要忘记强制转换!
-
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(!root){
//二叉查找树肯定是放在根节点上!!!
return new TreeNode(val);
}
if(root->val < val){
root->right = insertIntoBST(root->right, val);
}
else if(root->val > val){
root->left = insertIntoBST(root->left, val);
}
return root;
}第二次写这道题的时候必须记录一下:在二叉树的递归中,如果你需要一个dummy节点,那么这个dummy节点其实就在root->left = delete(root->left)中,此时这个root就是前置节点!!!这一点一定要记好了!!
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(!root){
return nullptr;
}
if(root->val == key){
if(!root->left && !root->right){
return nullptr;
}
else if(!root->left){
return root->right;
}
else if(!root->right){
return root->left;
}else{
TreeNode* tmp = root->right;
TreeNode* dummy = root;
while(tmp->left){
dummy = tmp;
tmp = tmp->left;
}
cout<<"dummy->val"<<dummy->val<<endl;
cout<<"tmp->val"<<tmp->val<<endl;
root->val = tmp->val;
//这点容易错 草他妈,要判断dummy是不是原来的节点
if(dummy == root){
dummy->right = tmp->right;
}
else if(dummy != root){
dummy->left = tmp->right;
}
}
}
if(root->val > key){
root->left = deleteNode(root->left, key);
}
if(root->val < key){
root->right = deleteNode(root->right, key);
}
return root;
}
};-
涉及到的数据结构
这道题主要涉及二叉搜索树BST的删除问题。这个问题我想了三个小时,难点在于节点的删除的代码上
BST节点删除要分成三种情况
-
第一种
当被删除的节点是叶子节点,即无左孩子也无右孩子时,直接删除即可,简单
-
第二种
当被删除的节点只包含左孩子或者右孩子时,删除也很简单
-
第三种
当被删除的节点同时包含左孩子或者右孩子。我们从被删除节点的右节点为起点,往左子树上找最后一个节点,画个图就知道了。
然后把这个几点的值和被删除节点的互换,把该节点删掉就行。
-
举个例子,比如给算法输入
n = 5,也就是说用{1,2,3,4,5}这些数字去构造 BST。根据 BST 的特性,根节点的左子树都比根节点的值小,右子树的值都比根节点的值大。
所以如果固定
3作为根节点,左子树节点就是{1,2}的组合,右子树就是{4,5}的组合。左子树的组合数和右子树的组合数乘积就是
3作为根节点时的 BST 个数。
这道题动态规划和递归都能写
-
动态规划
int numTrees(int n) { vector<int> vec(n+1, 0); vec[0] = 1; vec[1] = 1; for(int i = 2; i < n + 1; i++){ for(int j = 1; j <= i; j++){ vec[i] += vec[j - 1] * vec[i - j]; } cout<<vec[i]<<endl; } return vec[n]; }
注意,当有0个数的时候,可以构成一个BST,因为空树也是!!!!
-
递归(难)
-
迭代---不能用!
第95题是给出个数,这道题是求所有的二叉树
重要重要重要!!!
这道题的本质是考察如何构建二叉树的,我给出构建二叉树的递归方法,根节点去中间值,这样是平衡的。
//从1到n构建二叉树 public TreeNode createBinaryTree(int n){ return helper(1, n); } //左闭右闭 public TreeNode helper(int start, int end){ if(start > end) return null; // 这里可以选择从start到end的任何一个值做为根结点, // 这里选择它们的中点,实际上,这样构建出来的是一颗平衡二叉搜索树 int val = (start + end) / 2; TreeNode root = new TreeNode(val); root.left = helper(start, val - 1); root.right = helper(val + 1, end); return root; }
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<TreeNode*> res = {};
vector<TreeNode*> generateTrees(int n) {
if(!n){
return res;
}
return construct(1, n);
}
vector<TreeNode*> construct(int left, int right){
vector<TreeNode*> tmp;
if(left > right){
tmp.push_back(nullptr);
return tmp;
}
for(int i = left; i <= right; i++){
vector<TreeNode*> left_vec = construct(left, i-1);
vector<TreeNode*> right_vec = construct(i+1, right);
//获得了所有左子树和右子树后,我们要取里面的节点
for(auto l : left_vec){
for(auto r : right_vec){
//①把根节点放外面可以看到发现,所有以根节点为i的树长得一模一样
//②因为每个左右子树不止一个,每次在左右中各挑一个组成一个完整的树,所以每次需要新建一个root,所以需要放在循环内
//所以不能放外面
TreeNode* root = new TreeNode(i);
root->left = l;
root->right = r;
//注意,在递归中这个tmp返回的只是列表中的节点
//但是在遍历left节点和right节点组成的数组时,每个节点就变成了头结点了吧
tmp.push_back(root);
}
}
}
return tmp;
}
};简简单单双指针,注意0的个数和非0个数之间的关系
i=0跳过,当不等于0时候替换然后j++,这样当走完时候j的位置到最后一个元素这中间的这么多都是0的数量
void moveZeroes(vector<int>& nums) {
int n = nums.size();
int j = 0;
for(int i = 0; i < n; i++){
if(nums[i]){
nums[j] = nums[i];
j++;
}
}
while(j < n){
nums[j++] = 0;
}
}vector<vector<int>> matrixReshape(vector<vector<int>>& nums, int r, int c) {
vector<vector<int>> tmp(r, vector<int>(c));
vector<int> res;
int m = nums.size();
int n = nums[0].size();
if(m*n != r*c){
return nums;
}
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
res.push_back(nums[i][j]);
}
}
for(int i = 0; i < r; i++){
for(int j = 0; j < c; j++){
tmp[i][j] = res[i*c+j];
}
}
return tmp;
} int findMaxConsecutiveOnes(vector<int>& nums) {
int n = nums.size();
int max_count = 0;
int tmp = 0;
for(int i = 0; i < n; i++){
if(nums[i] == 1 ){
tmp++;
}else{
tmp=0;
}
max_count = max(tmp, max_count);
}
return max_count;
}定位到行,然后每一行遍历
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int n = matrix.size();
int m = matrix[0].size();
int target_row = 0;
for(int i = 0; i < n; i++){
if(matrix[i][m-1] > target){
target_row = i;
break;
}
else if(matrix[i][m-1] == target){
return true;
}
}
cout<<target_row<<endl;
for(int i = 0; i < m; i++){
if(matrix[target_row][i] == target){
return true;
}
}
return false;
}
}这两道题对于列来说都要从后往前啊!!!!
从后往前啊!!!从后往前!!!
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size();
int n = matrix[0].size();
int i = 0;
int j = n-1;
while(i < m && j >= 0){
if(matrix[i][j] == target){
return true;
}
else if(matrix[i][j] > target){
j--;
}else{
i++;
}
}
return false;
}直接调用API来做题的主要由排序和堆,优先队列这类题目
没必要自己造轮子,完全没必要
所以这类中的题只是碰见了放进去
/*****快排*****/
int findKthLargest(vector<int>& nums, int k) {
int n = nums.size();
quicksort(nums, 0, n-1);
for(auto i : nums){
cout<<i<<" ";
}
return nums[n-k];
}
int partition(vector<int>& nums, int left, int right){
int povit = nums[left];
int povit_index = left;
while(left < right){
while(nums[right] >= povit && left < right){
right--;
}
while(nums[left] <= povit && left < right){
left++;
}
if(left < right){
int temp = nums[right];
nums[right] = nums[left];
nums[left] = temp;
}
}
//swap
nums[povit_index] = nums[left];
nums[left] = povit;
return left;
}
void quicksort(vector<int>& nums, int left, int right){
if(left >= right){
return;
}
int povit = partition(nums, left, right);
quicksort(nums, left, povit-1);
quicksort(nums, povit+1, right);
}void sortColors(vector<int>& nums) {
quciksort(nums, 0, nums.size()-1);
}
int partition(vector<int>& nums, int l, int r){
int pivot = nums[l];
int pivot_index = l;
while(l < r){
while(l < r && nums[r] >= pivot){
r--;
}
while(l < r && nums[l] <= pivot){
l++;
}
if(l < r){
int temp = nums[l];
nums[l] = nums[r];
nums[r] = temp;
}
}
nums[pivot_index] = nums[l];
nums[l] = pivot;
return l;
}
void quciksort(vector<int>& nums, int l, int r){
if(l >= r){
return;
}
int pivot = partition(nums, l, r);
quciksort(nums, l, pivot - 1);
quciksort(nums, pivot + 1, r);
}int maximumGap(vector<int>& nums) {
int len = nums.size();
if(len < 2){
return 0;
}
quicksort(nums, 0, len - 1);
for(auto a : nums){
cout<<a<<" ";
}
int max = nums[1] - nums[0];
for(int i = 2; i < len; i++){
int tmp = nums[i] - nums[i-1];
max = tmp > max ? tmp : max;
}
return max;
}
int partion(vector<int>& nums, int l, int r){
int pivot = nums[l];
int pivot_index = l;
while(l < r){
while(l < r && nums[r] >= pivot){
r--;
}
while(l < r && nums[l] <= pivot){
l++;
}
if(l < r){
int tmp = nums[r];
nums[r] = nums[l];
nums[l] = tmp;
}
}
nums[pivot_index] = nums[l];
nums[l] = pivot;
return l;
}
void quicksort(vector<int>& nums, int l, int r){
if(l >= r){
return;
}
int pivot_index = partion(nums, l, r);
quicksort(nums, l, pivot_index -1);
quicksort(nums, pivot_index+1, r);
}+++
动态规划可以分为如下的四步:
确定dp数组以及含义
确定递推公式
确定dp数组初始化的值
确定遍历顺序
框架代码如下:
for 状态1 in 状态1的所有取值: for 状态2 in 状态2的所有取值: for ... dp[状态1][状态2][...] = 择优(选择1,选择2...)要明确状态和选择两个要素
int numTrees(int n) {
vector<int> vec(n+1, 0);
vec[0] = 1;
vec[1] = 1;
for(int i = 2; i < n + 1; i++){
for(int j = 1; j <= i; j++){
vec[i] += vec[j - 1] * vec[i - j];
}
cout<<vec[i]<<endl;
}
return vec[n];
}
int fib(int n) {
vector<int> dp (n+1, 0);
if(n == 0){
return 0;
}
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i < n+1 ; i++){
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}本问题其实常规解法可以分成多个子问题,爬第n阶楼梯的方法数量,等于 2 部分之和
- 爬上 n−1 阶楼梯的方法数量。因为再爬1阶就能到第n阶
- 爬上 n−2 阶楼梯的方法数量,因为再爬2阶就能到第n阶
int climbStairs(int n) {
vector<int> dp(n+1, 0);
if(n <= 2){
return n;
}
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i < n + 1; i++){
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}- 注意一点,在进行状态计算的时候,不要带条件,尽量if判断放到前面去做。
在首尾都加一个0 分别代表地面,和楼顶(地面和楼顶不消耗体力)
数组的每一个数字代表从当前楼梯迈出所需要耗费的体力
从地面开始,第一步可以选择第0阶或者第1阶,都不费力
最终要求到达最后一个0(楼顶)所耗费的体力最少。
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
if(n == 2){
return cost[0] > cost[1] ? cost[1] : cost[0];
}
int new_len = n + 2;
vector<int> new_cost(n+2, 0);
for(int i = 1; i <= n; i++){
new_cost[i] = cost[i-1];
}
int len = new_cost.size();
vector<int> dp(len+1, 0);
dp[0] = 0;
dp[1] = 0;
for(int i = 2; i < len+1; i++){
//重点在于,登上第i层,这个第i层是不算的,记住。
dp[i] = min(dp[i-1] + new_cost[i-1], dp[i-2]+ new_cost[i-2]);
}
return dp[len];
}
};没啥说的,简单
int uniquePaths(int m, int n) {
//要注意为什么是m,n而不是m+1,n+1。
//因为到第(m-1,n-1)的时候,第(m-1, n-1)不需要算路径
//第一行和第一列都是
vector<vector<int>> dp(m, vector<int>(n, 1));
for(int i = 1; i < m ; i++){
for(int j = 1; j < n; j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}-
注意事项
51 9这个情况的时候数组会越界,因此我们要把vector数组设置成long型就OK了(×)
发现了一个细思极恐的事情,之前的代码我把vect数组设置成(m+1,n+1)的勒,但是没出错,因为我return的是m-1和n-1,只跟m,n相关,其他无关啊!所以我之前代码还多算了很多。63题注意注意!
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
for(int i = 0; i < n && obstacleGrid[0][i] != 1; i++){
//第一行上有石头
dp[0][i] = 1;
}
for(int j = 0; j < m && obstacleGrid[j][0] != 1; j++){
//第一列上有石头
dp[j][0] = 1;
}
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
if(obstacleGrid[i][j] == 1){
dp[i][j] = 0;
}else{
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}
return dp[m-1][n-1];
}
};-
注意事项
-
这道题和63题不一样在于不能初始化为1了,不然太麻烦。初始化为0吧,然后第一行第一列设置为1,但是也不能大意,看第二个要点
-
[[1,0]],把障碍物放在入口,绝了我擦,注意如果第一行和第一列有障碍我,障碍物后面的都要设为0;
-
如果有障碍物,设为0就行,也不难
-
将 i 拆分成 j和 i−j 的和,且 i−j 不再拆分成多个正整数,此时的乘积是j×(i−j);
将 i 拆分成 j 和 i−j 的和,且 i−j 继续拆分成多个正整数,此时的乘积是j×dp[i−j]。
一个大小为i的数可以分为j和i-j ---------------------- | j | (i-j) | ----------------------
int integerBreak(int n) {
vector<int> dp(n+1);
dp[0] = 0;
dp[1] = 0;
for(int i = 2; i < n + 1; i++){
int MAX = 0;
//注意这里j<i,其实j<=(i/2)也是可以的
//因为i-j是逐步变小的,当i-j小于i/2的时候就自然舍弃掉了
for(int j = 1; j < i; j++){
MAX = max(max(j*(i-j),j*dp[i-j]), MAX);
}
dp[i] = MAX;
}
return dp[n];
}-
注意事项
这道题第二次做了还忘了,切记!!!
int numTrees(int n) {
vector<int> dp(n+1, 0);
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i < n + 1; i++){
for(int j = 1; j <= i; j++){
//记住,j是作为根节点的,所以j要从1开始
dp[i] += dp[j-1] * dp[i-j];
}
}
return dp[n];
} 排列组合问题,这道题还可以这样翻译:
楼梯的阶数一共为target,一次可以走的步数为nums[i]。 一共有多少种走法?
int combinationSum4(vector<int>& nums, int target) {
int n = nums.size();
vector<int> dp(target + 1, 0);
dp[0] = 1;
for(int i = 0; i < target + 1; i++){
for(auto num : nums){
if(i - num >= 0 && dp[i] < INT_MAX - dp[i -num]){
dp[i] += dp[i - num];
}
}
}
return dp[target];
}第518题使用二维数组写的,其实可以改写为1维数组,背包问题就用一维数组来做!
-
易错点
主要在于数组越界问题,这道题很巧妙,可以参考一下。
+++
背包模板:
- 0/1背包:外循环nums,内循环target,target倒序且target>=nums[i];
- 完全背包:外循环nums,内循环target,target正序且target>=nums[i];
- 组合背包:外循环target,内循环nums,target正序且target>=nums[i];
- 分组背包:这个比较特殊,需要三重循环:外循环背包bags,内部两层循环根据题目的要求转化为1,2,3三种背包类型的模板
组合问题公式
dp[i] += dp[i-num]
True、False问题公式
dp[i] = dp[i] or dp[i-num]
最大最小问题公式
dp[i] = min(dp[i], dp[i-num]+1)或者dp[i] = max(dp[i], dp[i-num]+1)
含义:从给定的物品中选取,可以选1,也可以不选0,使设计的方案达到某个价值。
状态转移方程:$f[i][j]$ = max(
$f[i - 1][j]$ ,$f[i - 1][j - weight[i] + value[i]$ )
问:给你一个可装载重量为W的背包和N个物品,每个物品有重量和价值两个属性。
其中第i个物品的重量为wt[i],价值为val[i],现在让你用这个背包装物品,最多能装的价值是多少?
N = 3 W = 4 wt = [2, 1, 3] val = [4, 2, 3]
#include<iostream>
#include<vector>
#include<string>
#include<algorithm>
using namespace std;
int max(int a,int b) {
return a > b ? a : b;
}
int main() {
int n = 3; //3个物品
int w = 4;//重量为4
vector<int> wt = { 2,1,3 };
vector<int> val = { 4,2,3 };
//dp[i][j]表示前i个物品,背包的容量为j时候的价值
vector<vector<int>> dp(n + 1, vector<int>(w + 1, 0));
for (int i = 1;i < n + 1;i++) {
for (int j = 1;j < w + 1;j++) {
//表示下一个加入背包的物品超过背包的容量,则不加
if (j-wt[i-1]<0) {
dp[i][j] = dp[i - 1][j];
}
else {
//在装第i个物品的前提下,背包能装的最大价值是多少?即dp[i-1][w-wt[i-1]+val[i-1]]
dp[i][j] = max(dp[i-1][j],dp[i-1][j-wt[i-1]]+val[i-1]);
}
}
}
cout << dp[n][w] << endl;
cout << "***************" << endl;
for (int i = 0;i < n + 1;i++) {
for (int j = 0;j < w + 1;j++) {
cout << dp[i][j] << " ";
}
cout << endl;
}
system("pause");
return 0;
}-
解题思路
首先,能分成两个相同的子集表明一个问题:这个集合中元素的和是偶数!!!。因此这道题就是01背包问题,即设计方案使得元素集合达到sum/2。
-
代码
bool canPartition(vector<int>& nums) { int n = nums.size(); int sum = 0; //for循环的另一种写法,比较简单 for(int& i : nums){ sum += i; } if(sum%2 != 0){ return false; } int target = sum / 2; //动态规划的关键是对dp数组的定义 //本题中dp数组表示把第i个物品放入背包,此时背包重量为j的bool值 //物品就是给的数组,重量就是对应的和的一半 vector<vector<bool>> dp(n+1, vector<bool>(target+1, false)); //当背包重量为0的时候,永远为true,这个要想一想 for(int i = 0; i < n+1; i++){ dp[i][0] = true; } for(int i =1 ; i < n + 1; i++){ for(int j = 1; j < target + 1; j++){ if(j - nums[i-1] < 0 ){ dp[i][j] = dp[i - 1][j]; }else{ //状态转移方程如下: //1.如果不把这第i个物品装入背包,那么能够恰好装满背包取决于上一个状态dp[i-1][j],继承之前的结果。 //2.如果把这第i个物品装入了背包,那么是否能够恰好装满背包,取决于状态dp[i - 1][j-nums[i-1]]。 dp[i][j] = dp[i - 1][j] || dp[i-1][j - nums[i-1]]; } } } return dp[n][target]; }
-
解题思路
这道题的难点就在于为什么能够转化成01背包问题。最后求的是数组中石头的可能最小重量,那是不是可以转换成如果是最小数量,那就把数组分成两堆,同时这两堆的差值最小!这本质就是个脑筋急转弯!
整个题目,每个回合数两两抽出来比较,两个数之差将被再一次扔到数组里面,继续上面的过程。每个回合都会丢失掉两个数字,加入一个新的数字,这个数字就是两个数的差。相当于来说,就是少了a和b,但是多了一个a-b,a,b就此消失,但是在下一回合,a-b可能又被抓出去pk,pk后a-b就此再消失了,又产生了新的一个差。那么每一步来说,其实就相当于a,b没有真正意义消失。 到了最后一回合,我们可以知道,其实找出两个最接近的数字堆。
总: (26+31+21) - (40+33) 这就是找出两个总和接近的两个堆。 如何让两个堆接近呢? 那就是沿着中间分两半,找左右各自那一半,那么思路就来到了找出一半堆这里。那么就自然而然地来到取不取的问题,就是01背包问题。
近一步想:把数组分成两堆,那么总数组和为sum,这两堆的差如果要最小,是不是应该每一堆都要接近sum/2?
在想一步:我们就需要让每一堆都尽可能接近sum/2,这样不就能保证两堆差最小
可以得出结论:两堆中出现一个最大值max_weight,那么最后的值就是sum-2*max_weight
-
代码
int lastStoneWeightII(vector<int>& stones) { int sum = accumulate(stones.begin(), stones.end(), 0); int target = sum / 2; int n = stones.size(); //dp数组的含义非常重要! //按照01背包典型的dp定义 //即前i个物品,背包容量为j vector<vector<int>> dp(n+1, vector<int>(target+1, 0)); for(int i = 1; i < n + 1; i++){ for(int j = 1; j < target + 1; j++){ if(j - stones[i -1] < 0){ dp[i][j] = dp[i -1][j]; }else{ //注意,第i个物品的索引值是stone[i-1]!!! dp[i][j] = max(dp[i -1][j], dp[i -1][j - stones[i -1]] + stones[i - 1]); } } } cout<<sum<<endl; cout<<target<<endl; cout<<dp[n][target]<<endl; return sum - 2 * dp[n][target]; }
-
注意点
- std::accumulate这个要会用,很方便
- 01背包这个模板要回,就按照这个dp数组的定义走
-
思路
这道题又他妈是移到脑筋急转弯,感觉碰到数组的题全是脑筋急转弯啊!
一般碰到这种数组题目,都要想一想
我们设有m个“+”,有n个“-”
所以正好之和绝对值为x,负号之和绝对值为y,有如下式子:
x+y=sum,x-y=target
可以得出x=(sum+target)/2
也就是说,有(sum+target)/2个正号即当前正号全部加起来为x时可以得到target,转换成01背包就是从数组中拿(sum+target)/2个达到target的重量
-
代码
int findTargetSumWays(vector<int>& nums, int target) { int len = nums.size(); int sum = std::accumulate(nums.begin(), nums.end(), 0); //注意点1:由于(sum+target)/2是表示所有+符号的和,也就是说这个数不能是奇数,必须是偶数 if((sum < target) || (sum + target) % 2 != 0){ return 0; } int goal = (target + sum) / 2; //注意点2:[100],target=-200的情况下,需要判断一下goal的正负 if(goal < 0){ return 0; } vector<vector<int>> dp(len+1, vector<int>(goal+1, 0)); //dp[i][0]=1因为目标是0的话不选就行,在这里goal表示的是所有+之和所以如果目标是0就是说前i个数全变成负号就行 dp[0][0] = 1; for(int i = 1; i < len + 1; i++){ for(int j = 0; j < goal +1; j++){ if(j - nums[i-1] < 0){ dp[i][j] = dp[i-1][j]; }else{ dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]]; } } } return dp[len][goal]; }
-
注意事项
在01背包问题中一定要明去dp数组的含义啊。
比如dp数组代表的是重量,则状态表达式可以是 $$ dp[i][j]=dp[i−1][j],j<nums[i-1]\ dp[i][j]=dp[i−1][j]+dp[i−1][j−nums[i-1]]+nums[i-1],j≥nums[i] $$ 如果dp数组表示的是组合数,比如dp[i][j]前i个数使得背包重量为j的个数这种,则状态表达式为 $$ dp[i][j]=dp[i−1][j],j<nums[i-1]\ dp[i][j]=dp[i−1][j]+dp[i−1][j−nums[i-1]],j≥nums[i] $$
思路:把总共的 0 和 1 的个数视为背包的容量,每一个字符串视为装进背包的物品。这道题就可以使用 0-1 背包问题的思路完成,这里的目标值是能放进背包的字符串的数量。
//用一个两个容量的数组保存0和1的值,绝了!
vector<int> count_one_zero(string& strs){
vector<int> dp(2, 0);
int n = strs.size();
for(int i = 0; i < n; i++){
if(strs[i] == '0'){
dp[0]++;
}
else if(strs[i] == '1'){
dp[1]++;
}
}
return dp;
}
int findMaxForm(vector<string>& strs, int m, int n) {
int len = strs.size();
vector<vector<vector<int>>> dp(len+1,vector<vector<int>>(m+1,vector<int>(n+1, 0)));
for(int i = 1;i < len + 1; i++){
vector<int> count_arr = count_one_zero(strs[i -1]);
int zero_count = count_arr[0];
int one_count = count_arr[1];
for(int j = 0; j < m + 1; j++){
for(int w = 0; w < n+1; w++){
if(j - zero_count >= 0 && w - one_count >= 0){
dp[i][j][w] = max(dp[i - 1][j][w],dp[i - 1][j - zero_count][w - one_count]+1);
}else{
dp[i][j][w] = dp[i - 1][j][w];
}
}
}
}
return dp[len][m][n];
}
/************************************************************************/
class Solution {
public:
vector<int> count(string& strs){
vector<int> vec(2, 0);
for(auto tmp : strs){
if(tmp == '0'){
vec[0]++;
}
if(tmp == '1'){
vec[1]++;
}
}
return vec;
}
int findMaxForm(vector<string>& strs, int m, int n) {
int len = strs.size();
vector<vector<vector<int>>> dp(len+1, vector<vector<int>>(m+1, vector<int>(n+1, 0)));
for(int i = 1; i < len + 1; i++){
vector<int> vec = count(strs[i-1]);
int zero = vec[0];
int one = vec[1];
//易错点2:必须从0开始,所以以后再有这些问题看看是否是从0开始的
for(int j = 0; j < m + 1; j++){
for(int z = 0; z < n + 1; z++){
//易错点1:必须是或,只要有一个越界就不行
if(j-zero < 0 || z - one < 0){
dp[i][j][z] = dp[i-1][j][z];
}else{
dp[i][j][z] = max(dp[i-1][j][z], dp[i-1][j-zero][z-one] + 1);
}
}
}
}
return dp[len][m][n];
}
};完全背包前瞻:有N种物品和一个容量为T的背包,每种物品都就可以选择任意多个,第i种物品的价值为P[i],体积为V[i],求解:选哪些物品放入背包,可卡因使得这些物品的价值最大,并且体积总和不超过背包容量。跟01背包一样,完全背包也是一个很经典的动态规划问题,不同的地方在于01背包问题中,每件物品最多选择一件,而在完全背包问题中,只要背包装得下,每件物品可以选择任意多件。从每件物品的角度来说,与之相关的策略已经不再是选或者不选了,而是有取0件、取1件、取2件...直到取⌊T/Vi⌋(向下取整)件。
01背包和完全背包的区别就在于一件物品能不能反复被取。在代码中就是dp[i][j]的状态和dp[i-1][j], dp[i-1][j-w[i-1]]还是dp[i-1][j], dp[i][j-w[i-1]]。仔细观察可以发现即是i(01背包)或者i-1(完全背包)。那么如果是一维数组的话,内循环是逆序(01背包),内循环不需要逆序(完全背包)
/**一维数组的写法,但是我感觉不好理解**/
int coinChange(vector<int>& coins, int amount) {
//dp[i]表示凑成总金额为i所需要的最小硬币个数
vector<int> dp(amount+1,amount+1);
dp[0] = 0;
int n = coins.size();
for(int i = 0; i < n; i++){
for(int j = 1; j < amount + 1; j++){
if(j - coins[i] >= 0){
dp[j] = min(dp[j],dp[j - coins[i]]+1);
}
}
}
//处理凑不出来amount的情况
if(dp[amount] == amount+1){
return -1;
}
return dp[amount];
}
/*二维数组*/
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int len = coins.size();
vector<vector<int>> dp(len+1, vector<int>(amount+1, 10001));
for(int i = 0; i < len + 1; i++){
dp[i][0] = 0;
}
for(int i = 1; i< len+1; i++){
for(int j = 0;j < amount+1; j++){
if(j - coins[i-1] >= 0){
//这句话才是完全背包和01背包的不同,和精髓
//不是i-1是因为完全背包的数可以重复取
dp[i][j] = min(dp[i-1][j], dp[i][j-coins[i-1]] + 1);
}else{
dp[i][j] = dp[i-1][j];
}
}
}
for(int i = 1; i < len + 1; i++){
for(int j = 0;j < amount+1;j++){
cout<<dp[i][j]<<" ";
}
cout<<endl;
}
return dp[len][amount] == 10001?-1:dp[len][amount];
}
};这道题的主要难点在于如何判断有些凑不到amount的情况。由于这道题动态规划求最小,我们就初始化dp数组最大,大于amount就可以了。那么如果dp[amount] = 初始化的那个值,说明我们凑不到 返回-1
int change(int amount, vector<int>& coins) {
int n = coins.size();
//dp[i][j]表示用前i个硬币凑齐j所需要的个数
vector<vector<int>> dp(n+1, vector<int>(amount+1, 0));
dp[0][0] = 1;
for(int i = 1; i < n + 1; i++){
for(int j = 0; j < amount + 1; j++){
if(j - coins[i -1] < 0){
dp[i][j] = dp[i - 1][j];
}else{
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i-1]];
}
}
}
return dp[n][amount];
}
/******二维数组会超时,但又不超时了 吐了!!!*****/
int change(int amount, vector<int>& coins) {
int len = coins.size();
vector<vector<int>> dp(len+1, vector<int>(amount+1, 0));
dp[0][0] = 1;
for(int i = 1; i < len + 1; i++){
for(int j = 0; j < amount+1; j++){
if(j-coins[i-1] >= 0){
dp[i][j] = dp[i][j-coins[i-1]] + dp[i-1][j];
}else{
dp[i][j] = dp[i-1][j];
}
}
}
return dp[len][amount];
}-
思路
比如说amount = 5, coins = [1, 2, 5],有4种方式可以凑成:
5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1观察这几种情况可以发现为啥用动态规划,比如5=2+2+1,那么组成2有多少种就可以查dp数组了,所以要用动态规划。
对于这道题其实关键点有两个
-
$dp[0][0] = 1$ ;当没硬币凑出0的情况为1,这个切记 - 第二个就是状态转移方程了。这道题问的是几种可能,因此只要是满足凑出j的都要加上才行(好好理解这句话)。
-
这道题其实是组合数,至于为啥是组合数,一定要结合377题来看。因为377题是有顺序要求的,因此事排列数
这道题暗含了一个数学定理即四平方定理: 任何一个正整数都可以表示成不超过四个整数的平方之和。 推论:满足四数平方和定理的数n(四个整数的情况),必定满足 n=4^a
int numSquares(int n) {
int upper_bound = (int)sqrt(n);
//记住!求最少的,dp数组一定要设置为最大!
vector<int> dp(n + 1, n + 1);
dp[0] = 0;
dp[1] = 1;
for(int i = 1; i < n + 1; i++){
for(int j = 1; j < upper_bound + 1; j++){
if(i - pow(j, 2) < 0){
dp[i] = dp[i];
}else{
dp[i] = min(dp[i],dp[i - pow(j, 2)] + 1);
}
}
}
return dp[n];
}做到这里回头再看背包问题的基本模板会发现一切都是那么简单,记住背包问题的模板!
-
注意的问题
这道题中我们可以总结出一些问题,即求最小值时初始化dp数组一定要最大才行,不能初始化0了
这道题有两个点。
- 对于c++中判断某个字符串是否在另一个数组中,就是用这种容器存储,然后
容器.find(str) != 容器.end()表明找到了,其他时候表明找不到。- 对于子串的问题,和普通的背包问题是不一样的。普通的背包问题我们外层遍历容量,内层遍历物品之类的。但是对于字符串,特别是这道题,抽象成背包问题时候,循环就要稍微变一下了。对于字符串问题,我们一定要遍历某一字符串的子串才行。比如说这道dp[i]表示前i个字符串是否能由字典中单词组成,这个时候我们不能遍历字典了,要遍历这前i个字符串的子串!切记,这是重点中的重点!
set<string> wordDict_set;
//好像vector也能判断,不用set
for(auto str : wordDict){
wordDict_set.insert(str);
}
//表示前n个单词是否可以表示出来
int n = s.size();
int m = wordDict.size();
vector<bool> dp(n+1, false);
dp[0] = true;
for(int i = 1 ; i < n + 1; i++){
for(int j = 0; j < i ; j ++){
string temp = s.substr(j,i-j);
if(dp[j] && wordDict_set.find(temp) != wordDict_set.end()){
dp[i] = true;
}
}
}
return dp[n];
}看到这道题的第一反应是所有奇数索引和偶数索引相加然后比较大小,但是仔细一想发现不太对。因为比如说:[3,2,4,9]这个数组最大值是3+9,所以跟奇偶没有任何关系
int rob(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n+1, 0);
dp[1] = nums[0];
for(int i = 2; i < n + 1; i++){
dp[i] = max(dp[i - 1], dp[i - 2]+nums[i - 1]);
}
return dp[n];
}-
总结一下
这道题还是比较简单的,中规中矩
还是照例分析一下思路吧。
这道题和上一道题的唯一区别就在于首尾也是相连的,仅此而已!
这就表明①如果我们选择了首家偷,就不能偷最后一家。②如果偷第二家,可以考虑最后一家。
因此我们可以把这个数组拆分成两种情况求最大值
每个数组当做打家劫舍1来做
int rob(vector<int>& nums) {
int n = nums.size();
if(n == 1){
return nums[0];
}
if(n == 2){
return nums[0] > nums[1] ? nums[0] : nums[1];
}
vector<int> nums_temp1(n-1);
vector<int> nums_temp2(n-1);
for(int i = 0; i < n - 1; i++){
nums_temp1[i] = nums[i + 1];
}
for(int i = 0; i < n - 1; i++){
nums_temp2[i] = nums[i];
}
int nums_temp1_rob = rob_with_nums(nums_temp1);
int nums_temp2_rob = rob_with_nums(nums_temp2);
return nums_temp1_rob > nums_temp2_rob ? nums_temp1_rob : nums_temp2_rob;
}
int rob_with_nums(vector<int>& nums_temp){
int n = nums_temp.size();
vector<int> dp(n+1, 0);
dp[1] = nums_temp[0];
for(int i = 2; i < n + 1; i++){
dp[i] = max(dp[i - 1], dp[i - 2] + nums_temp[i -1]);
}
return dp[n];
}严格来说这是一道二叉树的题
就只有两种情况呗,①偷根节点,②不偷根节点
其实代码很好写,但是会报超时错误!
下面来找一下原因:我们计算每个节点对应的最高金额,因此这里面也可以记忆化搜索,即父亲节点的最大金额其实不用再去重新算了,因为子节点的最大金额可以存起来,要是用的话直接用就好,这样可以节省很多时间。因此我们需要用一个key-value来存储每个节点对应的最大金额
map<TreeNode*, int> temp;
int rob(TreeNode* root){
if(!root){
return 0;
}
if(root->left == nullptr && root->right == nullptr){
return root->val;
}
if(temp.find(root) != temp.end()){
return temp[root];
}
int cash1 = root->val;
int cash2 = 0;
if(root->left != nullptr){
cash1 += rob(root->left->left) + rob(root->left->right);
}
if(root->right != nullptr){
cash1 += rob(root->right->left) + rob(root->right->right);
}
cash2 += rob(root->left) + rob(root->right);
int max_rob = max(cash1, cash2);
temp[root] = max_rob;
return max_rob;
}这又是一类动态规划题型,核心思路是对于数组$dp[i][j]$中的j只有0和1两种,表示卖或者不卖
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n+1, vector<int>(2, 0));
//具体细节,第一次情况要特别说明
//循环从第二天开始
dp[1][0] = 0;
dp[1][1] = -prices[0];
for(int i = 2; i < n + 1; i++){
dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i-1]);
//1表示有,有可能上一次的那个还没卖,或者重新买了(-prices)
dp[i][1] = max(dp[i-1][1], -prices[i-1]);
}
return dp[n][0];
}
//************贪心算法**************/
int maxProfit(vector<int>& prices) {
int n = prices.size();
int max_profit = 0;
int min_price = prices[0];
for(int i = 0; i < n; i++){
min_price = min(prices[i], min_price);
max_profit = max(max_profit, prices[i] - min_price);
}
return max_profit;
}int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n+1,vector<int>(2, 0));
dp[1][0] = 0;
dp[1][1] = -prices[0];
for(int i = 2; i < n + 1; i++){
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i-1]);
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i-1]);
}
return dp[n][0];
}总结一下:这道题和121题的区别在于这道题不限制交易的次数,因此可以无数次交易而不是1次
所以代码的区别主要在于如果这次买了,那么状态转移就是上一次就买了,或者上一次卖掉了$dp[i-1][0]$然后再买
只能一笔交易和不限制交易次数的情况比较好写,因为状态转移很简单,但是当多次的话,就要用三元组了
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<vector<int>>> dp(n+1,vector<vector<int>>(3, vector<int>(2, 0)));
for(int k = 0; k < 3; k++){
dp[1][k][0] = 0;
dp[1][k][1] = -prices[0];
}
for(int i = 2; i < n + 1; i++){
for(int k = 1; k < 3; k++){
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i-1]);
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i-1]);
}
}
return dp[n][2][0];
}-
注意事项
-
2次的话影响不能消除,必须用三元组写
-
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i-1]);这行代码中,因为我们求得是1即买入了,那么上次没买这次买了,这次买了k就要减一
-
-
注意事项
这道题和最多买卖两次是一模一样的思路就是把2换成k了但是还是有几个地方需要注意的
- 给的整数数组可能为0
- k其实没有很大,可以想一下,最多为n/2(n是数组的长度)
int maxProfit(int k, vector<int>& prices) {
int n = prices.size();
if(n == 0){
return 0;
}
k = min(k, n/2);
vector<vector<vector<int>>> dp(n+1,vector<vector<int>>(k+1, vector<int>(2, 0)));
//dp[1][k][0] = 0 && dp[1][k][1] = -prices[0]
for(int i = 0; i < k + 1; i++){
dp[1][i][0] = 0;
dp[1][i][1] = -prices[0];
}
for(int i = 2; i < n + 1; i++){
for(int j = 1; j < k + 1; j++){
dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i-1]);
dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i-1]);
}
}
return dp[n][k][0];
}-
注意事项
含冷冻期,说明一个事儿:即如果你买了的话,你必须是i-2买的,不能是i-1了!!!
int maxProfit(vector<int>& prices) {
int n = prices.size();
if(n == 0){
return 0;
}
//尽可能多的完成交易,也就说不限制次数
vector<vector<int>> dp(n+1, vector<int>(2, 0));
dp[1][0] = 0;
dp[1][1] = -prices[0];
for(int i = 2; i < n + 1; i++){
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i-1]);
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i-1]);
}
return dp[n][0];
}-
注意事项
有手续费而已,无非就是卖出的时候减去手续费,简单!
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
if(n == 0){
return 0;
}
vector<vector<int>> dp(n + 1, vector<int>(2, 0));
dp[1][0] = 0;
dp[1][1] = -prices[0];
for(int i = 2; i < n + 1; i++){
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i-1]- fee);
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i-1]);
}
return dp[n][0];
}子序列问题是常见的算法问题,而且并不好解决。
首先,子序列问题本身就相对子串、子数组更困难一些,因为前者是不连续的序列,而后两者是连续的,就算穷举你都不一定会,更别说求解相关的算法问题了。
而且,子序列问题很可能涉及到两个字符串,比如前文「最长公共子序列」,如果没有一定的处理经验,真的不容易想出来。所以本文就来扒一扒子序列问题的套路,其实就有两种模板,相关问题只要往这两种思路上想,十拿九稳。
一般来说,这类问题都是让你求一个最长子序列,因为最短子序列就是一个字符嘛,没啥可问的。一旦涉及到子序列和最值,那几乎可以肯定,考察的是动态规划技巧,时间复杂度一般都是 O(n^2)。
原因很简单,你想想一个字符串,它的子序列有多少种可能?起码是指数级的吧,这种情况下,不用动态规划技巧,还想怎么着?
既然要用动态规划,那就要定义 dp 数组,找状态转移关系。我们说的两种思路模板,就是 dp 数组的定义思路。不同的问题可能需要不同的 dp 数组定义来解决。
-
注意事项
贪心足以,不用动态规划了!
int findLengthOfLCIS(vector<int>& nums) {
int n = nums.size();
int max_len = 1;
int count = 1;
for(int i = 1; i < n ; i++){
if(nums[i] > nums[i-1]){
count++;
max_len = max(max_len, count);
}else{
count = 1;
}
}
return max_len;
}-
这道题动态规划不太好想,如果画个图会好一点,因此我就随便在网上找一张图了。
这张图对于理解二维dp数组很有帮助
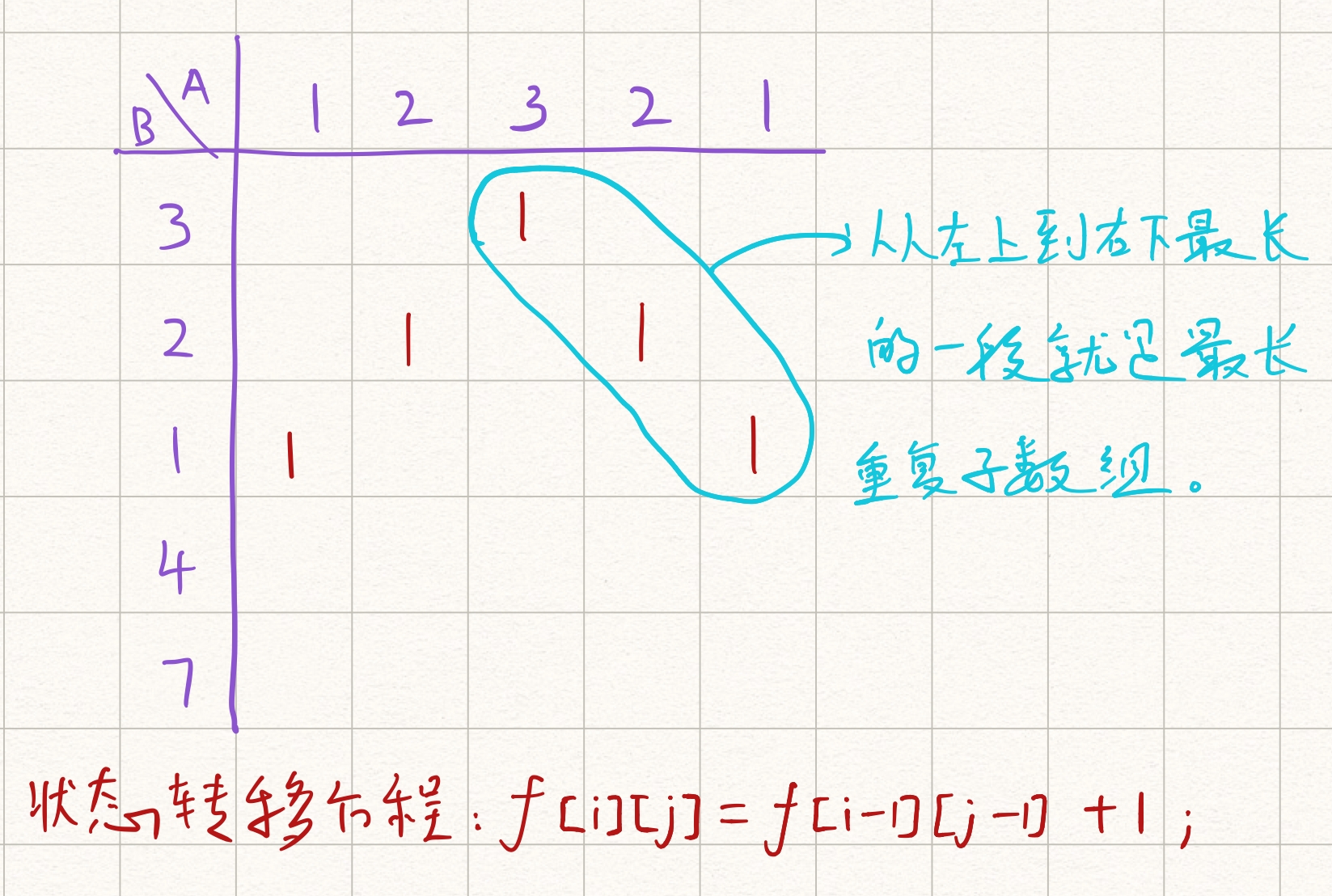
这里面$dp[i][j]$表示对于第一个数组前i个,和第二个数组前j个元素相等的数量,然后用一个max_com来存储个最大值,其实这种dp不太好想,还是画个dp来理解一下比较好
int findLength(vector<int>& nums1, vector<int>& nums2) {
int n1 = nums1.size();
int n2 = nums2.size();
int max_com = 0;
vector<vector<int>> dp(n1+1, vector<int>(n2+1, 0));
for(int i = 1; i < n1 + 1; i++){
for(int j = 1; j < n2 + 1; j++){
if(nums1[i-1] == nums2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
max_com = max(max_com, dp[i][j]);
}
}
}
return max_com;
}-
滑动窗口
int findLength(vector<int>& nums1, vector<int>& nums2) {
int n1 = nums1.size();
int n2 = nums2.size();
return n1 > n2 ? sliding(nums2, nums1) : sliding(nums1, nums2);
}
int sliding(vector<int>& short_vec, vector<int>& long_vec){
int n1 = short_vec.size();
int n2 = long_vec.size();
int max_repeat = 0;
//短的和长的数组的最右边对齐
for(int i = 1; i <= n1; i++){
int tmp = get_repeat(short_vec, 0, long_vec, n2-i,i);
cout<<"tmp1:"<<tmp<<endl;
max_repeat = max(tmp, max_repeat);
}
//短的和长的数组的最左边对齐
//以长数组的长度为参考
for(int i = n2; i - n1>=0; i-- ){
int tmp = get_repeat(short_vec, 0, long_vec, i-n1, n1);
cout<<"tmp2:"<<tmp<<endl;
max_repeat = max(tmp, max_repeat);
}
//短数组的右边和长数组的左边对齐
//以短数组的长度为参考
for(int i = n1; i >= 1; i--){
int tmp = get_repeat(short_vec, n1-i, long_vec, 0, i);
cout<<"tmp3:"<<tmp<<endl;
max_repeat = max(tmp, max_repeat);
}
return max_repeat;
}
int get_repeat(vector<int>& short_vec, int i, vector<int>& long_vec, int j, int common_len){
int max_repeat = 0;
int count = 0;
for(int index = 0; index < common_len; index++){
if(short_vec[i+index] == long_vec[j+index]){
count++;
max_repeat = max(count, max_repeat);
}else{
max_repeat = max(count, max_repeat);
count = 0;
}
}
return max_repeat;
} - 注意事项,这道题简单是简单,状态转移方程也不难。但是要记住这道题不是求得dp[n]!而是求dp数组的最大值
int maxSubArray(vector<int>& nums) {
//这道题一眼dp不解释
int n = nums.size();
vector<int> dp(n + 1, INT_MIN);
dp[1] = nums[0];
for(int i = 2; i < n + 1; i++){
dp[i] = max(dp[i-1]+nums[i-1], nums[i-1]);
}
int max_sum = INT_MIN;
for(auto n : dp){
max_sum = max(max_sum, n);
}
return max_sum;
}这道题第二次做的时候一时间没有想到还。之前我老是想着nums[i-1]与nums[i-2]做匹配,其实是不对的,因为相邻的两个数其实没什么关系,不能这样子比较
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n + 1, 1);
for(int i = 2; i < n + 1; i++){
for(int j = 1; j < i; j++){
if(nums[i - 1] > nums[j - 1]){
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
int max_sub = 0;
for(auto n:dp){
max_sub = max(max_sub, n);
}
return max_sub;
}
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n+1, 1);
int tmp = nums[0];
for(int i = 2; i < n + 1; i++){
int tmp = 1;
for(int j = 1; j < i; j++){
if(nums[i-1] > nums[j-1]){
tmp = max(tmp, dp[j] + 1);
}
}
dp[i] = tmp;
}
sort(dp.begin(), dp.end(), std::greater<int>());
return dp[0];
}二分
时间复杂度nlogn
维护一个结果数组,如果当前元素比结果数组的值都大的的话,就追加在结果数组后面(相当于递增序列长度加了1);否则的话用当前元素覆盖掉第一个比它大的元素(增长缓慢才可能是最长的)(这样做的话后续递增序列才有可能更长,即使并没有更长,这个覆盖操作也并没有副作用哈,当然这个覆盖操作可能会让最终的结果数组值并不是最终的递增序列值,这无所谓)
操作只有两个:覆盖和追加,只有大于最后一个元素才会追加,其他时候都是覆盖
//比较粗糙的二分,每次循环都求了res数组的大小,效率太低
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
vector<int> res;
res.push_back(nums[0]);
int tmp = nums[0];
for(int i = 1; i < n; i++){
if(nums[i] > tmp){
res.push_back(nums[i]);
tmp = nums[i];
}
else if(tmp == nums[i]){
continue;
}
else{
int index = lower_bound(res.begin(), res.end(), nums[i]) - res.begin();
cout<<"nums[i]:"<<nums[i]<<endl;
cout<<"index:"<<index<<endl;
res[index] = nums[i];
int n = res.size();
tmp = res[n-1];
}
}
return res.size();
}
//改进的二分
nt lengthOfLIS(vector<int>& nums) {
int n = nums.size();
vector<int> res;
res.push_back(nums[0]);
int count = 0;
for(int i = 1; i < n; i++){
int index = lower_bound(res.begin(), res.end(), nums[i]) - res.begin();
//之前用的是upper_bound,结果[4,10,4,3,8,9]未通过
if(index > count){
res.push_back(nums[i]);
count++;
}else{
res[index] = nums[i];
}
}
return res.size();
}-
最长公共子序列问题是一类问题,包括下面的583和712题,都是一样的
公共子序列,打表就能做出来了!!典型的打表题
-
以下是代码部分
int longestCommonSubsequence(string text1, string text2) { int n = text1.size(); int m = text2.size(); vector<vector<int>> dp(n+1, vector<int>(m+1, 0)); for(int i = 1; i < n + 1; i++){ for(int j = 1; j < m + 1; j++){ if(text1[i - 1] == text2[j - 1]){ dp[i][j] = dp[i-1][j-1] + 1; }else{ dp[i][j] = max(dp[i-1][j], dp[i][j-1]); } } } return dp[n][m]; }
-
思路:核心代码就是最长公共子序列,但是需要注意的是结果
就是如果说公共子序列为0,则需要两个字符串长度的才行
如果有,就是$n+m*2dp[n][m]$
int minDistance(string word1, string word2) {
int n = word1.size();
int m = word2.size();
vector<vector<int>> dp(n+1, vector<int>(m+1, 0));
for(int i = 1; i < n + 1; i++){
for(int j = 1; j < m + 1; j++){
if(word1[i - 1] == word2[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return n+m-2*dp[n][m];
}本质上换汤不换药~参考前面的公共子序列问题。
int minimumDeleteSum(string s1, string s2) {
int n = s1.size();
int m = s2.size();
vector<vector<int>> dp(n+1, vector<int>(m+1, 0));
int ascii_count = 0;
for(int i = 0; i < n; i++){
ascii_count += s1[i];
}
for(int i = 0; i < m; i++){
ascii_count += s2[i];
}
for(int i = 1; i < n + 1; i++){
for(int j = 1; j < m+1; j++){
if(s1[i-1] == s2[j-1]){
dp[i][j] = dp[i-1][j-1] + (int)s1[i-1];
}else{
dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
}
}
if(dp[n][m] == 0){
return ascii_count;
}
return ascii_count-2*dp[n][m];
}-
思路:本质就是求最长公共子序列!!!!!!
因为这道题两个连线不想交,你想想,如果不想交,不就是公共子序列,按顺序找吗???
leetcode真的恶心
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size();
int m = nums2.size();
vector<vector<int>> dp(n+1, vector<int>(m+1, 0));
for(int i = 1; i < n + 1; i++){
for(int j = 1; j < m + 1; j++){
if(nums1[i - 1] == nums2[j - 1]){
dp[i][j] = dp[i-1][j-1] + 1;
}else{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[n][m];
}-
思路:这道题很简单,但是道题给了另一个不简单的方向,即要匹配的字符串就数十亿个,如何考虑?
-
简单的:
脑瘫写法:
bool isSubsequence(string s, string t) { int n = s.size(); int m = t.size(); if(n == 0){ return true; } int temp = 0; for(int i = 0; i < m; i++){ if(s[temp] == t[i]){ temp++; if(temp == n){ return true; } } } return false; }
双指针:
bool isSubsequence(string s, string t) { int i = 0; int j = 0; int n = s.size(); int m = t.size(); while(i < n && j < m){ if(s[i] == t[j]){ i++; } j++; } return i == n; }
-
进阶数十亿的:
如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10 亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
空间换时间的思想。关键点是:利用一个二维数组记录每个位置的下一个要匹配的字符的位置,这里的字符是
'a' ~ 'z',所以这个数组的大小是dp[n][26],n 为 T 的长度。那么每处理一个子串只需要扫描一遍 S 即可,因为在数组的帮助下我们对 T 是“跳跃”扫描的。如下图一,很自然的,当T索引为0时候,对应的第0列就是当前字符在T中出现位置的下标,没有的标-1就行;
/*ahbgdc这个T字符串构成的数组如下:重点在于从后往前构造会简单很多*/ 1 -1 -1 -1 -1 -1 -1 3 3 3 -1 -1 -1 -1 6 6 6 6 6 6 -1 5 5 5 5 5 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 4 4 4 4 -1 -1 -1 2 2 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
这个图应该能说明思想,其实就是跳表的思想,只要有-1就不比了,不用完全遍历t,时间换空间的思想。
bool isSubsequence(string s, string t) { t.insert(0, ' '); int len = t.size(); vector<vector<int>> vec(len, vector<int>(26, 0)); //创建一个二维数组 for(char char_t= 'a'; char_t <= 'z'; char_t++){ int next_pos = -1;//这个要放在循环里面!不能放在外面! for(int i = len-1; i >=0 ;i--){ vec[i][char_t-'a'] = next_pos; if(t[i] == char_t){ next_pos = i; } } } //开始匹配 int index = 0; for(char c : s){ index = vec[index][c - 'a']; if(index == -1){ return false; } } return true; }
-
思路:
说句题外话,就是两个字符串或者数字比较的话,大概率不是dp就是双指针,dp的话ij表示s1的前i个和s2的前j个
同时,子序列或者字串的话,切记,空串是任何序列的子序列!
因此这道题也很常规,但是难点就在于状态转移方程不好想
首先给出状态转移方程:
if (s[i - 1] == t[j - 1]) { dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; } else { dp[i][j] = dp[i - 1][j]; }
状态转移方程为啥是上述的?只有一个办法,就是画表。以后看到子序列问题的dp ,画表就完事儿了!!!!
int numDistinct(string s, string t) { int n = s.size(); int m = t.size(); if(n < m){ return 0; } vector<vector<long long>> dp(n+1, vector<long long>(m+1, 0)); //切记!空字符串匹配为1 for(int i = 0; i < n + 1; i++){ dp[i][0] = 1; } for(int i = 1; i < n + 1; i++){ for(int j = 1; j < m + 1; j++){ if(s[i - 1] == t[j - 1]){ dp[i][j] = dp[i - 1][j - 1] + dp[i -1][j]; if(dp[i][j]>INT_MAX){ dp[i][j]=0; } }else{ dp[i][j] = dp[i - 1][j]; } } } return dp[n][m]; }
-
前面说过两个单词或者两个字符串的问题不是双指针就是动态规划问题,很明显这个这么难的问题就是动态规划。
同时又是两个字符串比较,那肯定$dp[i][j]$啊!主要是这个状态转移方程不太好想
当两个字符不相等的时候,有三种操作:删除、插入和替换!!!这才是状态转移方程的重点!!
当
word1[i] == word2[j],dp[i][j] = dp[i-1][j-1];当
word1[i] != word2[j],dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1其中,
dp[i-1][j-1]表示替换操作,dp[i-1][j]表示删除操作,dp[i][j-1]表示插入操作。
int third_min(int a, int b, int c){
int temp = a < b ? a : b;
return temp < c ? temp : c;
}
int minDistance(string word1, string word2) {
int n = word1.size();
int m = word2.size();
vector<vector<int>> dp(n+1, vector<int>(m+1, 0));
//确定完dp后还是得考虑极端情况
for(int i = 0; i < m + 1; i++){
dp[0][i] = i ;
}
for(int i = 0; i < n + 1; i++){
dp[i][0] = i ;
}
for(int i = 1; i < n + 1; i++){
for(int j = 1; j < m + 1; j++){
if(word1[i - 1] == word2[j - 1]){
dp[i][j] = dp[i - 1][j - 1];
}else{
dp[i][j] = third_min(
dp[i - 1][j - 1] + 1, //替换
dp[i - 1][j] + 1, //word1删除一个字符然后换和word2相同的,这个是一个操作
dp[i][j - 1] + 1 //word2删除一个字符然后换和word1相同的,这个是一个操作
);
}
}
}
return dp[n][m];
}首先回文子串问题涉及到的都是单个字符串,所以如果是单个字符串用动态规划的基本都是二维的,i-j
其次,回文字符串,都是从后往前遍历的,这个要记住。因为dp的状态转移方程特性决定的
还是用动态规划吧,中心扩散没太看懂
说一下自己的想法,因为就单个字符串,因此我之前说过单个字符串的话是要有范围的。
为什么外循环会从len-1开始,对于字符串“cabac来说”,如果s[0]的c=s[4]的c,那么只需要看“aba”即可,如果你的for循环从0开始的换,你都从0过来了还看什么aba,只有从后往前,才能看aba吧
int countSubstrings(string s) {
int len = s.size();
vector<vector<bool>> dp(len, vector<bool>(len, false));
int count = 0;
for(int i = len - 1; i >= 0; i--){
for(int j = i; j < len; j++){
if(s[i] == s[j] ){
if(j-i <= 1){
count++;
dp[i][j] = true;
}
else if(dp[i + 1][j - 1]){
count++;
dp[i][j] = true;
}
}
}
}
return count;
}思路:这道题一定要和647放在一起看,这两道题是一模一样的类型。
这道题的难点主要在于dp的状态转移过程,来分析一下
如果s[i]与s[j]相同,那么$dp[i][j] = dp[i + 1][j - 1] + 2$,因为回文串的个数嘛,+2
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为$dp[i + 1][j]$
加入s[i]的回文子序列长度为$dp[i][j - 1]$
那么dp[i][j]一定是取最大的,即:$dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])$
int longestPalindromeSubseq(string s) {
int len = s.size();
vector<vector<int>> dp(len+1, vector<int>(len+1, 0));
for(int i = 1; i < len + 1; i++ ){
dp[i][i] = 1;
}
for(int i = len ; i >= 1; i--){
//这里j从i+1开始,和上一题不一样,因为不考虑本身
for(int j = i + 1; j < len+1; j++){
if(s[i-1] == s[j-1]){
dp[i][j] = dp[i+1][j-1] + 2;
}else{
//不构成回文串了,不能+1了
dp[i][j] = max(dp[i][j-1], dp[i+1][j]);
}
}
}
return dp[1][len];
}另类的DP套路!
最重要的是下面的这张图:
- 注意事项,一定要注意两层是$dp[i][j]=a$,三层的话肯定是最里面一层for有个变量temp,然后跳开里面这层才是dp赋值
int superEggDrop(int k, int n) {
//dp数组的含义是到第n层有k个鸡蛋可以进行的最小的操作次数
vector<vector<int>> dp(n+1, vector<int>(k+1, 0));
for(int i = 1; i < k + 1; i++){
dp[1][i] = 1;
}
//一个鸡蛋扔肯定每楼扔一次
for(int i = 1; i < n + 1; i++){
dp[i][1] = i;
}
for(int i = 2; i < n + 1; i++){
for(int j = 2;j < k + 1; j++){
//楼层区间
int temp = INT_MAX;
for(int m = 1; m <= i; m++){
//最坏就是最大
temp = min(temp, max(dp[m-1][j-1], dp[i-m][j])+1);
}
dp[i][j] = temp;
}
}
return dp[n][k];
}这样子写会超时!不过重要的是思路
-
第二种思路!!!!
其实第二种思路最主要的就是对于dp数组的设计了,dp设计好了一道题也就自然而然的解开了
我们把dp设计成$dp[i][j]$表示有i个鸡蛋,走了m步能到的层数,因此$dp[i][j]$就是层数,只要层数大于等于n,就可以返回j
状态转移方程这样理解:
当我们扔鸡蛋的时候,都是两种情况,碎或者不碎,不管碎没碎,都用掉了一步(+1),
无论你在哪层楼扔鸡蛋,鸡蛋只可能摔碎或者没摔碎,碎了的话就测楼下,没碎的话就测楼上。
无论你上楼还是下楼,总的楼层数 = 楼上的楼层数 + 楼下的楼层数 + 1(当前这层楼)
因此$dp[i][j]$的i是次数,不管碎没碎总是i-1!!
至于为啥初始化dp数组的时候要用k+1和n+1是因为最多次数不可能超过楼层数吧!!!
int superEggDrop(int k, int n) { vector<vector<int>> dp(n+1, vector<int>(k+1, 0)); for(int i = 1; i < n + 1; i++){ for(int j = 1; j < k + 1; j++){ dp[i][j] = dp[i-1][j]/*鸡蛋没碎,注意这里面i是次数!*/ + dp[i-1][j-1]/*鸡蛋碎了*/ + 1; if(dp[i][j] >= n){ return i; } } } return n; }
-
思路分析,其实这道题dp应该这样定义,即$dp[i][j]$指的是区间i到j中,所得到的气球的最大值。
那么经过前面的洗礼,我们很自然而然的就会想到在i和j之间用一个参数k来分割,因此自然而然是三个for循环,然后
$dp[i][j] = max(dp[i][j], 状态转移)$ 很自然而然
但是这道题很经典在于,k这个气球是最后一个被戳爆的,一定要记住!!!
根据状态转移方程可以画一下图,看看求$dp[i][j]$需要先求那一行一列,很清楚明白
int maxCoins(vector<int>& nums) {
int n = nums.size();
vector<int> temp_nums(n+2);
temp_nums[0] = 1;
for(int i = 0; i < n ; i++){
temp_nums[i+1] = nums[i];
}
temp_nums[n+1] = 1;
vector<vector<int>> dp(n+2, vector<int>(n+2, 0));
for(int i = n; i >= 0; i--){
for(int j = i + 1; j < n + 2; j++){
for(int k = i + 1; k < j; k++){
dp[i][j] = max(dp[i][j], dp[i][k]+dp[k][j]+(temp_nums[k]* temp_nums[i]* temp_nums[j]));
}
}
}
return dp[0][n+1];
}寻找最优解问题,一般将求解过程分成若干个步骤,每个步骤都应用贪心原则,当前(局部)最优的选择,从局部最优策略扩展到全局的最优解。基本步骤如下:
- 从某个初始解出发
- 采用迭代的过程,当可以向目标前进一步时,根据局部最优策略,得到一部分解然后缩小问题规模
- 将所有解综合起来。
- 简单的贪心算法,排序+双指针
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
cout<<g[0]<<endl;
int i = 0;
int j = 0;
int g_size = g.size();
int s_size = s.size();
int count = 0;
while(i < g_size && j <s_size){
if(g[i] <= s[j]){
i++;
j++;
count++;
}else{
j++;
}
}
return count;
}-
刚开始想着从小到大排序然后把小的变成负的就行,但是这样是有问题的,因为没有考虑负数的问题。
因此思路变成,计算一个数组中负数的个数,然后和k次比较,如果k大于负数的个数m,则将所有负数变成整数然后重新排序。
如果k小于负数的个数m,则最小的负数变成正数就行
int largestSumAfterKNegations(vector<int>& nums, int k) {
int neg_num = 0;
int len = nums.size();
int sum = 0;
for(int i = 0; i < len; i++){
if(nums[i] < 0){
neg_num++;
}
}
sort(nums.begin(), nums.end());
if(k > neg_num){
//先把负数变成正数
for(int i = 0; i < neg_num; i++){
nums[i] = -nums[i];
}
k = (k - neg_num) % 2;
//接下来全部变成正数数组
sort(nums.begin(), nums.end());
for(int i = 0; i < k; i++){
nums[i] = -nums[i];
}
for(int i = 0; i < len; i++){
sum+=nums[i];
}
}else{
for(int i = 0; i < k; i++){
nums[i] = -nums[i];
}
for(int i = 0; i < len; i++){
sum+=nums[i];
}
}
return sum;
}bool lemonadeChange(vector<int>& bills) {
int len = bills.size();
if(bills[0] != 5){
return false;
}
//注意只有5,10,20的面值
int five = 0;
int ten = 0;
int twenty = 0;
int temp = 0;
for(int i = 0; i < len; i++){
if(bills[i] == 5){
five++;
}
else if(bills[i] == 10){
ten++;
}
else if(bills[i] == 20){
twenty++;
}
temp = bills[i] - 5;
if(temp == 5){
five--;
}
else if(temp == 15){
//更倾向于10+5这种方式找零
if(ten > 0 ){
ten--;
five--;
}else{
five = five - 3;
}
}
if(five < 0 || ten < 0 || twenty <0){
return false;
}
}
return true;
}-
贪心算法: 局部最优然后达到全局最优
这道题想到错了这么多次
首先要注意,峰值最右边的永远有1个,因此count初值=1,但是这道题为什么卡这么久,因为首先越界不报错,我真是服了,第二就是判定条件,一定要看仔细!!!!
int wiggleMaxLength(vector<int>& nums) {
//峰值法
int pre = 0;
int now = 0;
int n = nums.size();
if(n <= 1){
return n;
}
int count = 1;
for(int i = 0; i < n-1 ; i++){
now = nums[i+1] - nums[i];
if((pre <= 0 && now > 0) || (pre >= 0 && now < 0)){
count++;
pre = now;
}
}
return count;
}-
思路:如果说是暴力破解的话,肯定是不可以的。
可以考虑局部最优,单调递增就意味着最后一位最大为9。
本来我没有加flag标志位,代码如下:
int monotoneIncreasingDigits(int n) { string str_num = to_string(n); int len = str_num.size(); if(n < 10){ return n; } for(int i = len - 1; i > 0; i--){ if(str_num[i] < str_num[i-1]){ cout<<"str_num[i]:"<<str_num[i]<<endl; cout<<"str_num[i-1]:"<<str_num[i-1]<<endl; str_num[i] = '9'; cout<<"str_num[i]:"<<str_num[i]<<endl; cout<<"str_num[i-1]:"<<str_num[i-1]<<endl; str_num[i-1]--; } } return stoi(str_num);
这样写是错误的,遇见100这个用例就知道了,进入if的时候i为1,因此要加一个flag标志位,从该标志为往后都设置为9!
代码如下:
int monotoneIncreasingDigits(int n) {
string str_num = to_string(n);
int len = str_num.size();
if(n < 10){
return n;
}
int flag = len;
for(int i = len - 1; i > 0; i--){
if(str_num[i] < str_num[i-1]){
flag = i;
str_num[i-1]--;
}
}
for(int i = flag; i < len; i++){
str_num[i] = '9';
}
return stoi(str_num);
}-
思路
“相邻的孩子中评分高的孩子必须获得更多的糖果”这句话拆分成为了两个规则:
-
从数组左边开始遍历,当
ratings[i] > rating[i-1]时,则必须保证第i个孩子的糖果比第i-1个的多这个是后比较是不完整的,比如说
[1,0,2]这个数组,只比较了0,1和2,0,对于0,2和1,0这个顺序没有对比 -
因此还要从数组的右边开始遍历,比对一次,当
ratings[i] > ratings[i]+1的时候,保证第i个孩子的糖果比第i+1个的多
因此加入有个数组时
[1,0,2],左边开始遍历得到数组[1,1,2],右边开始遍历的到数组[2,1,1],对于两个数组的同一个索引取最大值,即2+1+2=5。 -
-
代码
int candy(vector<int>& ratings) { int n = ratings.size(); if(n <= 1){ return 1; } vector<int> left(n, 1); vector<int> right(n, 1); for(int i = 1; i < n; i++){ if(ratings[i] > ratings[i - 1]){ left[i] = left[i - 1] + 1; } } for(int i = n - 2; i >= 0; i-- ){ if(ratings[i] > ratings[i + 1]){ right[i] = right[i + 1] + 1; } } int candy_num = 0; for(int i = 0; i < n; i++){ candy_num +=max(left[i], right[i]); } return candy_num; }
-
思路:
这道题就是排序,让数组变得有意义起来
思路很简单,首先根据第一个值倒序排序,因为第二个值的含义是前面有多少个大于等于第一个值的人,因此我们肯定先倒序。然后看第二个值,依次遍历数组,第二个值和索引比较,大于等于索引的就push_back,小于的就insert。
-
代码:
//加static是因为my_function函数其实有三个形参,第三个是this指针,但是sort中只用到了两个参数,参数不匹配 //所以要加static,因为static成员函数没有this指针 static bool my_function(vector<int>& vec1, vector<int>& vec2){ return vec1[0] > vec2[0] || (vec1[0] == vec2[0] && vec1[1] < vec2[1]); } vector<vector<int>> reconstructQueue(vector<vector<int>>& people) { sort(people.begin(), people.end(), my_function); vector<vector<int>> temp; for(int i = 0; i < people.size(); i++){ if(people[i][1] >= i){ temp.push_back(people[i]); }else{ temp.insert(temp.begin() + people[i][1], people[i]); } } return temp; }
-
补充
当数组时(key,value)类似类型的时候如何比较大小?我写到了代码集合里面
-
思路
其实这道题应该换个问法,即通过下面数组的跳跃规则,最多可以跳多远?这样如果跳出去最远超过了数组长度,直接返回true就好了,小于数组长度说明跳不到最后一个格子。
-
代码
bool canJump(vector<int>& nums) { int jump_to_index = 0; int n = nums.size(); for(int i = 0; i < n ; i++){ if(i > jump_to_index){ return false; } jump_to_index = max(jump_to_index, i + nums[i]); } return true; }
首先我觉得这个题用“能跳跃到的索引”表示是最好的,因为
i + nums[i]指的就是能够跳跃到的最大的索引。有了上面这个理解下面就好理解很多,之前代码错就是将for里面的判断语句放到了下面,其实应该先判断在计算,先判断就表明对于下一个索引,
jump_to_index能否到达。
-
思路
贪婪贪婪,选择一个能调的最远的往下走,肯定就是最小值了
-
代码
int jump(vector<int>& nums) { int jump_to_index = 0; int end_index = 0; int step = 0; int n = nums.size(); for(int i = 0; i < n-1; i++){ jump_to_index = max(jump_to_index, i+nums[i]); if(i == end_index){ step++; end_index = jump_to_index; } } return step; }
i < n-1是因为最后一次到达最后一个位置就不用再跳跃了。为什么是
i == end_index,因为题目上说了“假设你总是可以到达数组的最后一个位置”,因此我总能到达最后一个位置,不用考虑越界的情况
-
思路:
我们就根据上图这个例子来分析一下:
- 气球1和气球2是重叠的,需要一个箭,然后我们分析气球3
- 当气球1和气球2重叠的时候可以看到,气球1和气球2的空间应该合并成[2,6]然后再和气球3作比较
- 从上面特点可以看出,我们只需要关注气球的最右边界,找到右边界值最小的,成为新的右边界,然后再和气球3比
- 所以每次右边界改变就行
以上就是这套题的全部思路,一般这种题第一肯定是先排序再说其他。
-
代码
static bool compare(vector<int>& v1, vector<int>& v2){ return v1[0] < v2[0] || (v1[0] == v2[0] && v1[1] > v2[1]); } int findMinArrowShots(vector<vector<int>>& points) { int n = points.size(); sort(points.begin(), points.end(), compare); for(int i = 0; i < n; i++){ cout<<points[i][0]<<","<<points[i][1]<<" "<<endl; } int count = 1; for(int i = 0; i < n - 1 ; i++){ if(points[i][1] < points[i + 1][0]){ count++; }else{ points[i + 1][1] = min(points[i][1], points[i+1][1]); } } return count; }
-
思路
很简单,计算能连续的区间有多少个,取差就行
注意是移除最小区间数量,也就意味着我们尽可能少的移动区间,所以可以想一下,当你的
intervals[i][1]约小,你能减少的区间就越小,当你的intervals[i][1]越大,表明你要移除更多的区间才行。 -
代码
bool static cmp(vector<int>& v1, vector<int>& v2){ //return v1[0] < v2[0] || (v1[0] == v2[0] && v1[1] < v2[1]); return v1[1] < v2[1]; } int eraseOverlapIntervals(vector<vector<int>>& intervals) { int n = intervals.size(); //sort(intervals.begin(), intervals.end(), cmp); sort(intervals.begin(), intervals.end(), cmp); int end = INT_MIN; int count = 0; for(int i = 0; i < n ; i++){ cout<<intervals[i][0]<<" "<<intervals[i][1]<<endl; } for(int i = 0; i < n ; i++){ if(end <= intervals[i][0]){ end = intervals[i][1]; cout<<"end:"<<end<<endl; count++; } } cout<<"count:"<<count<<endl; return n - count; }
-
思路
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
-
代码
vector<int> partitionLabels(string S) { int len = S.size(); vector<int> distance(26); /*求每个字母*/ for(int i = 0; i < len; i++){ distance[S[i] - 'a'] = i; } int start = 0; int end = 0; vector<int> res; for(int i = 0; i < len; i++){ end = max(end, distance[S[i] - 'a']); if(i == end){ int tmp = end - start + 1; start = end + 1; res.push_back(tmp); } } return res; }
-
思路
这个题比之前那个射气球好点在于重叠不用考虑几个区间都重叠部分,只要有重叠就可以合并
要特别注意这个用例:[[2,3],[4,5],[6,7],[8,9],[1,10]]
-
代码
static bool cmp(vector<int>& v1, vector<int>& v2){ return v1[0] < v2[0] || (v1[0] == v2[0]) && (v1[1] < v2[1]); } vector<vector<int>> merge(vector<vector<int>>& intervals) { int len = intervals.size(); if(len <= 1){ return intervals; } vector<vector<int>> tmp1; sort(intervals.begin(), intervals.end(), cmp); int i = 0; /*每个元素是长度为2的int数组*/ vector<int> tmp2(2); /*首先初始化里面的数组,让其为第一个索引的数组值*/ tmp2[0] = intervals[0][0]; tmp2[1] = intervals[0][1]; /*用for也行*/ while(i < len - 1){ /*在这里的判断条件不是intervals[i][1] >= intervals[i+1][0]*/ /*因为这种类型都要保存右边最大的那个索引,参考射气球的那一道题*/ /*因此我认为记录最大索引值,是这种题的精髓*/ if(tmp2[1] >= intervals[i+1][0]){ tmp2[1] = max(intervals[i+1][1], tmp2[1]); }else{ tmp1.push_back(tmp2); tmp2[0] = intervals[i+1][0]; tmp2[1] = max(intervals[i+1][1],tmp2[1]); } i++; } tmp1.push_back(tmp2); return tmp1; }
-
思路
这道题之所以困扰我这么久并不是因为状态状态转移方程,这个其实很好理解
而是max即返回连续最大和 与 dp之间的关系
我之前一直以为要返回dp数组某个值,导致动态规划出现问题,但是其实这道题的max和dp是平行的,max是一个独立的变量,
比如
-2 1 -3这个例子,当i=3时dp的值行该是max(dp[i-1]+nums[i-1], nums[i-1])注意这个求得可不是某个区间的最大值,而某个区间的最大值在max中存储,因此还需要一步max=max(dp[i], max),这道题最关键的就是这一步。 -
代码
int maxSubArray(vector<int>& nums) { int n = nums.size(); if(n <= 1){ return nums[0]; } vector<int> dp(n+1, -10000); int max_num = nums[0]; dp[1] = nums[0]; for(int i = 2; i < n+1; i++){ dp[i] = max(dp[i-1] + nums[i-1], nums[i-1]); max_num = max(max_num, dp[i]); } return max_num; }
-
这题第一反应肯定是每个索引作为一个起点走一遍,这种方法也不能说出,但可能面试官不认,所以你得弄点新活儿。
思路:①一定能跑完全程,表明总加油数大于等于油耗数。②计算每个站的为起始点的剩余油量,会发现一个规律就是从站i开始到站j邮箱里面的油就是站i到站j的剩余油量相加,即cost[i]+...+cost[j]。③如果前面邮箱是负的,那么后面肯定是正的,因为要跑完全程啊,就得那么多,肯定要大于等于0才行。
因此,如果区间i-j的剩余油量和为负数,那么就从j+1开始算起。
-
代码
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) { int n = gas.size(); int rest_sum = 0; int rest_total = 0; int start = 0; for(int i = 0; i < n; i++){ rest_sum += gas[i]-cost[i]; //这个rest_total就是说计算所有剩余邮箱的和是否小于0的,放在里面不用再循环一下了,一次循环就解决了 rest_total += gas[i] - cost[i]; if(rest_sum < 0){ rest_sum = 0; start = i + 1; } } //只有剩余邮箱和小于0才会饶不了一圈 if(rest_total < 0){ return -1; } return start; }
需要经常的刷
对于回溯算法的总结和概括,有两个说的特别好。
接下来我准备总结一下他俩的精华
-
回溯算法的定义
回溯算法又叫做回溯搜索算法,主要是一种搜索方式,主要用在决策树类型的问题上。因此如果用回溯算法,就要遍历所有可能性,然后会返回所有可能,针对这些可能我们再做打算。因此可以看到,回溯是和递归相辅相成的,回溯可以说是递归的副产物。
-
回溯的效率
回溯算法的效率不高。
因为回溯会访问每一个节点,根据这个节点在访问下一个节点,因此本质上就是穷举。穷举本身能解决很多问题,有时候很多问题不得不用穷举来做做。
-
回溯算法解决的问题
-
组合问题:N个数里面按一定规则找出k个数的集合
-
排列问题:N个数按一定规则全排列,有几种排列方式
-
切割问题:一个字符串按一定规则有几种切割方式
-
子集问题:一个N个数的集合里有多少符合条件的子集
-
棋盘问题:N皇后,解数独等等
注意,排列和组合是不同的概念。排列是要注意顺序,而组合不用。
-
-
对回溯法的理解
回溯法解决的问题都可以抽象为树形结构
算法从宽度和深度两个层面递进,集合的大小就是树的宽度,递归的深度就是树的深度。
-
模板
回溯就是决策树的遍历过程,在这个过程中需要思考三个问题:
- 路径。已经做出的选择
- 选择列表。当前可以做的选择
- 结束条件。到达决策树底层,直接return
函数起名为back_tracing
返回值一般为void
参数的选取不固定,要具体问题具体分析
下图表现得最为直观:
代码模板如下:
void backtracking(参数) { if (终止条件) { 存放结果; return; } for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { 处理节点(做选择); backtracking(路径,选择列表); // 递归 回溯,撤销处理结果 } }
vector<vector<int>> res;
vector<int> temp;
vector<vector<int>> permute(vector<int>& nums) {
vector<bool> use_check(nums.size(), false);
back_tracing(nums, use_check);
return res;
}
void back_tracing(vector<int>& nums, vector<bool>& use_check){
if(temp.size() == nums.size()){
res.push_back(temp);
return;
}
for(int i = 0; i < nums.size(); i++ ){
//列表中的这个元素用过了,直接跳过
if(use_check[i] == true){
continue;
}
//列表中的这个元素还没有用
use_check[i] = true;
temp.push_back(nums[i]);
back_tracing(nums, use_check);
temp.pop_back();
use_check[i] = false;
}
}-
主要的问题
-
对于vector来说我们不需要new,因为vectorr的空间是自动增长的,它自己管理的,也是自己释放,不需要new
-
这道题对节点问题的处理主要在于判断是否是用过的节点。针对这中情况我们设一个vector,长度和给的列表长度一样长,里面初始化为false。如果某个元素用过了我们就用true表示。
当递归到决策树的最后一个节点后,会回溯,撤销处理结果,因此这个时候我们需要重新吧所有的全部初始化为false,重新使用。放入路径中的元素也全部拿出来,这里用的是vector c++11 的pop_back()方法。
-
不用去想具体实现步骤,就是只关注那个功能区写具体代码就行。
-
这道题和前面那道题的区别是这道题不能重复,因为给的序列可能会重复
vector<vector<int>> res;
vector<int> temp;
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<bool> user_check_vec(nums.size(), false);
sort(nums.begin(), nums.end());
back_tracing(nums, user_check_vec);
return res;
}
void back_tracing(vector<int>& nums, vector<bool> vec){
if(temp.size() == nums.size()){
res.push_back(temp);
return;
}
for(int i = 0; i < nums.size(); i++){
if(i > 0 && nums[i-1] == nums[i] && vec[i -1] == false){
continue;
}
if(vec[i] == true){
continue;
}
vec[i] = true;
temp.push_back(nums[i]);
back_tracing(nums,vec);
//回溯
temp.pop_back();
vec[i] = false;
}
}-
注意的问题
最开始我是这样想的,为了让第一个加入进去的元素不重复,我用一个map保存不重复的元素,用一个我设置为true。反正这样子不行,不去想了,有点难。
然后就是作者的思路:
if(i > 0 && nums[i-1] == nums[i] && vec[i-1] == false){ continue; }
这句话保证了不重复,是不是非常精妙!
nums[i-1] == nums[i]这句话保证了这次选的元素和上次选的一样,但是可能是同一层也有可能是同一个枝。我们要吧同一层的去掉,因此还要加上vec[i-1] == false。这句话保证了在递归算法中,与当前元素相同的前一个元素是没有用过的!!!切记,递归函数上面的代码不要想着回溯 !
当然做这道题之前一定要先排序,先排序!!!
重复的话就是排列问题,i不用指定。后面的基本都是i=start
下面这幅图就是本题的思路
vector<vector<int>> res;
vector<int> temp;
vector<vector<int>> combine(int n, int k) {
back_tracing(n ,k, 1);
return res;
}
void back_tracing(int n, int k, int start){
if(temp.size() == k){
res.push_back(temp);
return;
}
for(int i = start; i <= n; i++){
temp.push_back(i);
back_tracing(n, k, i+1);
temp.pop_back();
}
}重点,第二次写还是遇到了相同的问题
这是一道基本的组合问题,最最基本。这道题出问题的点在于不能出现像[2,2]或者[3,2]这样的组合
对于[2,2]这样的,我们必须要保证同一个树枝下,上一个要小下一个才行,
对于[3,2]这样的,我们必须保证同一层,前一个要小于后一个才行
不然的话写这道题的时候最开始会出现[[1,1],[1,2],[1,3],[1,4],[2,2],[2,3],[2,4],[3,2],[3,3],[3,4],[4,2],[4,3],[4,4]]这样的答案,苦死很久没发现为什么
其实问题出在for循环中 back_tracing(n, k, i+1);这段代码
对于同一树枝下的递归来说,我们考虑for时候,主要放在循环变量i上,而不是start上,因为start是控制层的递进。而i是控制递归的递进!!
第二次写补充: for 选择 in 选择列表 其实由于是组合问题,所以每次选择列表都要少一个数,因为不能重复!所以选择列表必须要i+1
在组合问题中,需要设置一个start变量。因为在递归层中,start决定从哪个索引开始遍历
每次从集合中选取元素,可选择的范围都在进行收缩,调整可选择的范围靠的就是start
vector<vector<int>> res;
vector<int> temp;
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
back_tracing(candidates, 0, 0, target);
return res;
}
void back_tracing(vector<int>& candidates,int sum, int start, int target){
if(sum == target){
res.push_back(temp);
return;
}
else if(sum > target ){
return;
}
for(int i = start; i < candidates.size(); i++){
temp.push_back(candidates[i]);
sum += candidates[i];
back_tracing(candidates, sum, i, target);
sum -= candidates[i];
temp.pop_back();
}
}-
重点总结
这道题和77题组合问题的相同点和难点主要在于下面这几行代码:
for(int i = start; i <= n; i++){ //处理节点 back_tracing(n, k, i+1); /**或者**/ back_tracing(n, k, i) //回溯 }
如果递归函数有个参数是i+1的话,则在递归层遍历中,取的值是不包含本身的下一个。
比如1 2 3 4,横向层次取1时候下次层递归的时候
- i+1:应该选择2 3 4
- i:应该选择1 2 3 4
横向层次取2的时候
- i+1: 应选择 3 4
- i:应选择 2 3 4
和47题条件一样,但是本质是属于求组合数的。
vector<vector<int>> res;
vector<int> temp;
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
int len = candidates.size();
sort(candidates.begin(), candidates.end());
vector<bool> is_used(len, false);
back_tracing(candidates, target, len, 0, 0, is_used);
return res;
}
void back_tracing(vector<int>& candidates, int target, int len, int start, int sum, vector<bool>& is_used){
if(sum == target){
res.push_back(temp);
return;
}
else if(sum > target){
return;
}
for(int i = start; i < len; i++){
//这道题和47题特别想,一个是排列一个是组合
//关键就在于i=start还是i=1
if(i > 0 && is_used[i-1]==false && candidates[i-1] == candidates[i]){
continue;
}
temp.push_back(candidates[i]);
is_used[i] = true;
sum += candidates[i];
back_tracing(candidates, target, len, i+1, sum, is_used);
sum -= candidates[i];
temp.pop_back();
is_used[i] = false;
}
}vector<vector<int>> res;
vector<int> temp;
vector<vector<int>> combinationSum3(int k, int n) {
vector<int> num = {1,2,3,4,5,6,7,8,9};
back_tracing(num, n ,k ,0, 0);
return res;
}
void back_tracing(vector<int>& num, int n, int k, int sum, int start){
if(temp.size() == k && sum == n){
res.push_back(temp);
return;
}
else if(sum > n){
return;
}
for(int i = start; i < num.size(); i++){
temp.push_back(num[i]);
sum += num[i];
back_tracing(num, n, k, sum, i+1);
sum -= num[i];
temp.pop_back();
}
}跟40题很相似,基本一样,但是已经排好序了没有重复,所以不用考虑重复的问题。
这道题的思路不要太简单,主要有两个点:一个函数用来判断是否是回文,一个用来分割字符串。
vector<string> tmp;
vector<vector<string>> res;
vector<vector<string>> partition(string s) {
int len = s.size();
back_tracing(s, len, 0);
return res;
}
void back_tracing(string s, int len, int start){
if(start >= len){
res.push_back(tmp);
return;
}
for(int i = start; i < len; i++){
string tmp_str = s.substr(start, i-start+1);
if(is_palindrome(tmp_str)){
tmp.push_back(tmp_str);
}else{
//重要!!!
continue;
}
back_tracing(s, len, i+1);
tmp.pop_back();
}
}
bool is_palindrome(string& str){
int len = str.size();
if(len == 1){
return true;
}
int l = 0;
int r = len - 1;
while(l < r){
if(str[l] == str[r]){
l++;
r--;
}else{
return false;
}
}
return true;
}-
涉及到的知识
-
判断是否回文,有字符串,链表的。字符串的判断就是如上代码,一个while循环,一个从0开始,一个从最后一个位置索引开始,依次比较是否相等
-
分割字符串,需要递归遍历,用到了回溯算法。这里面有几个值得注意的点
-
if中结束条件。这个题如果有满足的想加入到vector数组中,苦思冥想,不知道该什么时候加入。这道题给了我们思路,当遍历原始字符串长度大于的时候就结束了了!为啥等于呢,因为最后一位单个肯定是回文字符串
-
截取子串是substt(pos, pos+count),注意是[pos, pos+count],包括两端。
同时这个count是长度,所以在代码中表现为
i - start +1。
-
-
(字节)93. 复原 IP 地址
跟上题分割回文串一样的思路,我们先分割字符串。但是ip地址一共有四个段,所以我们的temp数组只要存储有四段string字符串就可以开始判断,如果满足ip地址的要求就加入,不满足就return;
vector<string> res;
vector<string> tmp;
vector<string> restoreIpAddresses(string s) {
int len = s.size();
back_tracing(s, len, 0);
return res;
}
void back_tracing(string s, int len, int start){
if(start == len && tmp.size() == 4){
string str_ip = tmp[0];
for(int i = 1; i < 4; i++){
str_ip = str_ip + "." + tmp[i];
}
res.push_back(str_ip);
return;
}
if(start < len && tmp.size() == 4){
return;
}
for(int i = start; i < len; i++){
//分割子串,这里是重点!!!
string str_tmp = s.substr(start , i - start + 1);
if(!jarge(str_tmp)){
break;
}
cout<<"str_tmp"<<str_tmp<<endl;
tmp.push_back(str_tmp);
back_tracing(s, len, i+1);
tmp.pop_back();
}
}
bool jarge(string s){
if(s.size() > 1 && s[0] == '0'){
return false;
}
int a = atoi(s.c_str());
if(a > 255){
return false;
}
return true;
}-
存在的问题
-
第一点是最开始我们用temp变量来存储分割出来满足ip的字符串,但是这会存在一个问题,当我们回溯的时候,不好去删除
string temp之前加入进来的值,这个真的不好删除,特别不好写,所以这样不行。另外一个思路是用vector数组来存储,这样回溯的时候可以pop。 -
ip地址共有四段,但是第四段不好截取。因此我们就在if中判断,如果有三段之后,随后一段截取就很方便,如代码
string last = s.substr(start, s.size() -1);如果last符合ip规则,我们temp数组就有四段,可以拼接到一起如果last不满足,则直接返回,temp数组回溯的时候也一次出来
-
for循环时候,还是要i+1,因为递归层不能重复取当前值,而是从下一个值开始取得
-
"111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111"这个回答会超时,记住要判定string长度大于13直接pass!
-
-
c++知识点
- 截取子串是substr(pos, pos+count)
- string转换成int用的是stoi,但是切记stoi能转换的最大数组长度到10,因此要判断如果string长度大于10就直接返回,肯定不满足,当时一直在这个点报错。
组合问题,分割问题都是关注叶子节点,而子集问题却要关注树的每个节点,都要遍历到。
同样不能出现重复,因此for循环从start开始
vector<vector<int>> res;
vector<int> temp;
vector<vector<int>> subsets(vector<int>& nums) {
back_tracing(nums, 0);
return res;
}
void back_tracing(vector<int>& nums, int start){
res.push_back(temp);
for(int i = start; i < nums.size(); i++){
temp.push_back(nums[i]);
back_tracing(nums, i+1);
temp.pop_back();
}
}跟78题比较,主要是在去重上
vector<vector<int>> res;
vector<int> temp;
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
vector<bool> use_check(nums.size(), false);
sort(nums.begin(), nums.end());
back_tracing(nums, 0, use_check);
return res;
}
void back_tracing(vector<int>& nums, int start, vector<bool>& use_check){
res.push_back(temp);
for(int i = start; i <nums.size(); i++ ){
if(i > 0 && nums[i] == nums[i-1] && use_check[i-1] == false){
continue;
}
temp.push_back(nums[i]);
use_check[i] = true;
back_tracing(nums, i+1, use_check);
temp.pop_back();
use_check[i] = false;
}
}-
总结
去重主要由两种:
-
不加use_check数组
if(i > 0 && nums[i] == nums[i-1]){ continue; }
不加use_check数组的话,对于同一层元素,如果有重复我们就是不能用它,如下图:
对于同一树枝来说,第三层得自己[1 ,2],第四层的[1, 2, 2]如果不加use_check数组,肯定得不到122这个数组,当if判断的时候就跳过了,但我们还要用到2,所以上述代码不合适。
-
加use_check数组
if(i > 0 && nums[i] == nums[i-1] && use_check[i-1] == false){ continue; }
used[i - 1] == true,说明同一树支candidates[i - 1]使用过
used[i - 1] == false,说明同一树层candidates[i - 1]使用过
而我们要对同一树层使用过的元素进行跳过。
-
vector<vector<string>> res;
vector<vector<string>> solveNQueens(int n) {
vector<string> chess(n, string(n, '.'));
back_tracing(chess, 0, n);
return res;
}
void back_tracing(vector<string>& chess, int row, int n ){
if(row == n){
res.push_back(chess);
return;
}
for(int col = 0; col < n ; col++){
if(!is_suit(chess, row, col, n)){
continue;
}
chess[row][col] = 'Q';
back_tracing(chess, row + 1, n);
chess[row][col] = '.';
}
}
bool is_suit(vector<string>& chess, int row, int col, int n){
//检查该列是否有冲突
for(int i = 0; i < row; i++ ){
if(chess[i][col] == 'Q'){
return false;
}
}
//检查左上
for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--,j--){
if(chess[i][j] == 'Q'){
return false;
}
}
//检查右上
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++){
if(chess[i][j] == 'Q'){
return false;
}
}
return true;
}- c++知识点
-
vector<string> chess(n, string(n, '.'))这是初始化的一种即string(n, '.')这种形式
-
N皇后问题是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来来遍历列,然后一行一列确定皇后的唯一位置。
本题就不一样了,本题中棋盘的每一个位置都要放一个数字,并检查数字是否合法,解数独的树形结构要比N皇后更宽更深。
在树形图中可以看出我们需要的是一个二维的递归(也就是两个for循环嵌套着递归)
一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!
解数独可以说是非常难的题目了,如果还一直停留在单层递归的逻辑中,这道题目可以让大家瞬间崩溃。
所以我在开篇就提到了二维递归,这也是我自创词汇,希望可以帮助大家理解解数独的搜索过程。
一波分析之后,在看代码会发现其实也不难,唯一难点就是理解二维递归的思维逻辑。
void solveSudoku(vector<vector<char>>& board) {
back_tracing(board);
return;
}
bool back_tracing(vector<vector<char>>& board){
for(int row = 0; row < 9; row++){ //遍历行
for(int col = 0; col < 9; col++){ //遍历列
if(board[row][col] != '.'){
continue;
}
for(char k = '1'; k <= '9'; k++){ //每个位置都有9种可能
if(!is_suit(board, col, row, k)){
continue;
}
board[row][col] = k;
if(back_tracing(board)){ //如果找到合适一组立刻返回
return true;
}
board[row][col] = '.';
}
return false; // 表示9个数都试完了,都不行,那么就返回false
}
}
return true;
}
bool is_suit(vector<vector<char>>& board, int col, int row, char k){
//判断行
for(int i = 0; i < 9; i++){
if(board[row][i] == k){
return false;
}
}
//判断列
for(int i = 0; i < 9; i++){
if(board[i][col] == k){
return false;
}
}
//判断9宫格
//要找到在第几个9宫格中
int start_row = (row / 3) * 3; //起始row
int start_col = (col / 3) * 3; //起始col
for(int i = start_row; i < start_row + 3; i++){
for(int j = start_col; j < start_col + 3; j++){
if(board[i][j] == k){
return false;
}
}
}
return true;
}需要再写一遍,阿里笔试出现过,第一次写不太会,要多看看
这道题的意思是就点击一次,然后看看点击一次后棋盘是什么样子的。
为啥会用dfs呢,因为当你挖出的不是雷后,要判断挖出的这个地方周围是否有雷,如果挖出的这个地方的四周(上下左右对角八个方向)有,则显示对应的地雷数目,如果是0则,就需要将该块改成B,并递归的处理其周围的八个块,所以需要用递归哦,这个是重点
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {
int x = click[0];
int y = click[1];
dfs(board, x, y);
return board;
}
void dfs(vector<vector<char>>& board, int x, int y){
//表示点击到了一个地雷
if(board[x][y] == 'M'){
board[x][y] = 'X';
return;
}
//如果不是地雷,判断挖开的地方周围有几个地雷
int mine_num = get_mine(board, x, y);
//挖开的这个块周边有地雷,则显示地雷数
if(mine_num > 0){
board[x][y] = mine_num + '0';
}
//周围都没有地雷,需要把该块周围的八个块都遍历一遍
else if(mine_num == 0){
board[x][y] = 'B';
//上
if((x-1) >=0 && board[x-1][y] == 'E'){
dfs(board, x-1, y);
}
//下
if((x+1) <= board.size() - 1 && board[x+1][y] == 'E'){
dfs(board, x+1, y);
}
//左
if((y-1) >= 0 && board[x][y-1] == 'E'){
dfs(board, x, y-1);
}
//右
if((y+1) <= board[0].size() - 1 && board[x][y+1] == 'E'){
dfs(board, x, y+1);
}
//左上
if((x-1) >= 0 && (y-1) >= 0 && board[x-1][y-1] == 'E'){
dfs(board, x-1, y-1);
}
//左下
if((x+1) <= board.size() - 1 && (y-1) >= 0 && board[x+1][y-1] == 'E'){
dfs(board, x+1, y-1);
}
//右上
if((x-1) >= 0 && (y+1) <= board[0].size() - 1 && board[x-1][y+1] == 'E'){
dfs(board, x-1, y+1);
}
//右下
if((x+1) <= board.size() - 1 && (y+1) <= board[0].size() - 1 && board[x+1][y+1] == 'E'){
dfs(board, x+1, y+1);
}
}
}
int get_mine(vector<vector<char>>& board, int x, int y){
int count = 0;
//上
if((x-1) >=0 && board[x-1][y] == 'M'){
count++;
}
//下
if((x+1) <= board.size() - 1 && board[x+1][y] == 'M'){
count++;
}
//左
if((y-1) >= 0 && board[x][y-1] == 'M'){
count++;
}
//右
if((y+1) <= board[0].size() - 1 && board[x][y+1] == 'M'){
count++;
}
//左上
if((x-1) >= 0 && (y-1) >= 0 && board[x-1][y-1] == 'M'){
count++;
}
//左下
if((x+1) <= board.size() - 1 && (y-1) >= 0 && board[x+1][y-1] == 'M'){
count++;
}
//右上
if((x-1) >= 0 && (y+1) <= board[0].size() - 1 && board[x-1][y+1] == 'M'){
count++;
}
//右下
if((x+1) <= board.size() - 1 && (y+1) <= board[0].size() - 1 && board[x+1][y+1] == 'M'){
count++;
}
return count;
}挺难的,没时间写了
vector<string> res;
string tmp;
vector<string> letterCombinations(string digits) {
unordered_map<char, string> m_map{
{'1', ""},
{'2', "abc"},
{'3', "def"},
{'4', "ghi"},
{'5', "jkl"},
{'6', "mno"},
{'7', "pqrs"},
{'8', "tuv"},
{'9', "wxyz"}
};
if(digits.size() == 0){
return res;
}
back_tracing(m_map, digits, 0);
return res;
}
void back_tracing(unordered_map<char, string>& m_map, string digits, int index){
if(index == digits.size()){
res.push_back(tmp);
return;
}
string tel_str = m_map[digits[index]];
for(int i = 0; i < tel_str.size(); i++ ){
tmp += tel_str[i];
back_tracing(m_map, digits, index+1);
tmp.pop_back();
}
}这个题其实和之前有一点区别,即不用考虑if了,直接全部加进去,在每个string上面修改
vector<string> res;
vector<string> letterCasePermutation(string s) {
dfs(s, 0);
return res;
}
void dfs(string s, int index){
res.push_back(s);
for(int i = index; i < s.size(); i++){
//这个回溯的重点不是pop_back了,而是大小写切回去
if(is_digital(s[i])){
continue;
}
change(s[i]);
dfs(s, i+1);
change(s[i]);
}
}
bool is_digital(char c){
if(c >= '0' && c <= '9'){
return true;
}
return false;
}
void change(char& c){
if(c >= 'a' && c <= 'z'){
c = (char)(c - 32);
}
else if(c >= 'A' && c <= 'Z'){
c = (char)(c + 32);
}
}这道题广度优先遍历也很好写,可以通过这个问题理解一下为什么回溯算法都是深度优先遍历,并且都用递归来写。
如果左括号数量不大于 nn,我们可以放一个左括号。如果右括号数量小于左括号的数量,我们可以放一个右括号。对,就是这样的
vector<string> res;
string tmp;
vector<string> generateParenthesis(int n) {
dfs(n, 0, 0);
return res;
}
void dfs(int n, int left, int right){
if(tmp.size() == 2*n){
res.push_back(tmp);
return;
}
if(left < n){
tmp += '(';
dfs(n, left+1, right);
tmp.pop_back();
}
if(right < left){
tmp += ')';
dfs(n, left, right+1);
tmp.pop_back();
}
}需要再写一遍,阿里笔试出现过,第一次写不太会,要多看看
这道题的意思是就点击一次,然后看看点击一次后棋盘是什么样子的。
为啥会用dfs呢,因为当你挖出的不是雷后,要判断挖出的这个地方周围是否有雷,如果挖出的这个地方的四周(上下左右对角八个方向)有,则显示对应的地雷数目,如果是0则,就需要将该块改成B,并递归的处理其周围的八个块,所以需要用递归哦,这个是重点
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {
int x = click[0];
int y = click[1];
dfs(board, x, y);
return board;
}
void dfs(vector<vector<char>>& board, int x, int y){
//表示点击到了一个地雷
if(board[x][y] == 'M'){
board[x][y] = 'X';
return;
}
//如果不是地雷,判断挖开的地方周围有几个地雷
int mine_num = get_mine(board, x, y);
//挖开的这个块周边有地雷,则显示地雷数
if(mine_num > 0){
board[x][y] = mine_num + '0';
}
//周围都没有地雷,需要把该块周围的八个块都遍历一遍
else if(mine_num == 0){
board[x][y] = 'B';
//上
if((x-1) >=0 && board[x-1][y] == 'E'){
dfs(board, x-1, y);
}
//下
if((x+1) <= board.size() - 1 && board[x+1][y] == 'E'){
dfs(board, x+1, y);
}
//左
if((y-1) >= 0 && board[x][y-1] == 'E'){
dfs(board, x, y-1);
}
//右
if((y+1) <= board[0].size() - 1 && board[x][y+1] == 'E'){
dfs(board, x, y+1);
}
//左上
if((x-1) >= 0 && (y-1) >= 0 && board[x-1][y-1] == 'E'){
dfs(board, x-1, y-1);
}
//左下
if((x+1) <= board.size() - 1 && (y-1) >= 0 && board[x+1][y-1] == 'E'){
dfs(board, x+1, y-1);
}
//右上
if((x-1) >= 0 && (y+1) <= board[0].size() - 1 && board[x-1][y+1] == 'E'){
dfs(board, x-1, y+1);
}
//右下
if((x+1) <= board.size() - 1 && (y+1) <= board[0].size() - 1 && board[x+1][y+1] == 'E'){
dfs(board, x+1, y+1);
}
}
}
int get_mine(vector<vector<char>>& board, int x, int y){
int count = 0;
//上
if((x-1) >=0 && board[x-1][y] == 'M'){
count++;
}
//下
if((x+1) <= board.size() - 1 && board[x+1][y] == 'M'){
count++;
}
//左
if((y-1) >= 0 && board[x][y-1] == 'M'){
count++;
}
//右
if((y+1) <= board[0].size() - 1 && board[x][y+1] == 'M'){
count++;
}
//左上
if((x-1) >= 0 && (y-1) >= 0 && board[x-1][y-1] == 'M'){
count++;
}
//左下
if((x+1) <= board.size() - 1 && (y-1) >= 0 && board[x+1][y-1] == 'M'){
count++;
}
//右上
if((x-1) >= 0 && (y+1) <= board[0].size() - 1 && board[x-1][y+1] == 'M'){
count++;
}
//右下
if((x+1) <= board.size() - 1 && (y+1) <= board[0].size() - 1 && board[x+1][y+1] == 'M'){
count++;
}
return count;
}又是笔试出现过的题目
感觉这道题和扫雷那道题好像啊,但是只能从上下左右四个方向
思路就是每一个都遍历一遍,board中的每一个都当做起始位置试一下
bool exist(vector<vector<char>>& board, string word) {
int row = board.size();
int col = board[0].size();
bool result = true;
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(dfs(board, word, i, j, 0)){
//只要有一个就直接返回
return true;
}
}
}
return false;
}
bool dfs(vector<vector<char>>& board, string word, int row, int col, int index){
//不匹配就不要浪费时间直接返回
if(board[row][col] != word[index]){
return false;
}
//遍历到word的最后一个后,说明都对了,返回
if(index == word.size() - 1){
return true;
}
//对于已经搜索过得标识一下,提高效率
char tmp = board[row][col];
board[row][col] = '#';
//上
if(row - 1 >= 0 && board[row - 1][col] != '#'){
if(dfs(board, word, row - 1, col, index + 1)){
return true;
}
}
//下
if(row + 1 <= board.size() - 1 && board[row + 1][col] != '#'){
if(dfs(board, word, row + 1, col, index + 1)){
return true;
}
}
//左
if(col - 1 >= 0 && board[row][col - 1] != '#'){
if(dfs(board, word, row, col - 1, index + 1)){
return true;
}
}
//右
if(col + 1 <= board[0].size() - 1 && board[row][col +1] != '#'){
if(dfs(board, word, row, col + 1, index + 1)){
return true;
}
}
board[row][col] = tmp;
return false;
}这道题刚读到题目的时候我的思路是,不看边上的,就看中间的。如果是这样的思路的话,后面就错了
因为本质上,如果四条边上出现O的话表示必定是不满足的,即不会被X包围。
所以我们只需要看四条件上的O即可,但是有一种情况是一条边上的某个O和内部的O相连如下:
XXXXX
XXOXX
XXOOX
XXXOX
上述这种情况下O是没有被X包围的,也会出现问题的。
所以我们的思路应该是仅仅遍历边上的O,然后如果某个O有相邻的O的话就遍历下去
对该点的上下左右点均进行领土扩张般的遍历 若满足条件则直接置'Y' 最终 棋盘格上除了'Y'以外的地方全部置'X'
void solve(vector<vector<char>>& board) {
int row = board.size();
int col = board[0].size();
for(int i = 0; i < col; i++){
dfs(board, 0, i);
}
for(int i = 0; i < col; i++){
dfs(board, row - 1, i);
}
for(int i = 0; i < row; i++){
dfs(board, i, 0);
}
for(int i = 0; i < row; i++){
dfs(board, i, col - 1);
}
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(board[i][j] != '#'){
board[i][j] = 'X';
}
}
}
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(board[i][j] == '#'){
board[i][j] = 'O';
}
}
}
}
void dfs(vector<vector<char>>& board, int row, int col){
if(board[row][col] == 'X'){
return;
}
board[row][col] = '#';
//上
if(row - 1 >= 0 && board[row - 1][col] == 'O'){
dfs(board, row - 1, col);
}
//下
if(row + 1 < board.size() && board[row + 1][col] == 'O'){
dfs(board, row + 1, col);
}
//左
if(col - 1 >= 0 && board[row][col - 1] == 'O'){
dfs(board, row, col - 1);
}
//右
if(col + 1 < board[0].size() && board[row ][col + 1] == 'O'){
dfs(board, row, col + 1);
}
}vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) {
int row = image.size();
int col = image[0].size();
int flag = image[sr][sc];
if(image[sr][sc] == newColor){
return image;
}
dfs(image, sr, sc, newColor, flag);
return image;
}
void dfs(vector<vector<int>>& image, int row, int col, int newColor, int flag){
image[row][col] = newColor;
//上
if(row - 1 >= 0 && image[row-1][col] == flag){
dfs(image, row - 1, col, newColor, flag);
}
//下
if(row + 1 <= image.size() - 1 && image[row+1][col] == flag){
dfs(image, row + 1, col, newColor, flag);
}
//左
if(col - 1 >= 0 && image[row][col-1] == flag){
dfs(image, row, col - 1, newColor, flag);
}
//右
if(col + 1 <= image[0].size() - 1 && image[row][col + 1] == flag){
dfs(image, row, col + 1, newColor, flag);
}
} 这道题最开始想的是如何计算岛屿数量,其实后来想了一下就是双循环中如果=1就进入dfs, 那么=1必定会形成一个岛屿,就可以计数了
int numIslands(vector<vector<char>>& grid) {
int row = grid.size();
int col = grid[0].size();
int count = 0;
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(grid[i][j] == '1'){
count++;
dfs(grid, i, j);
}
}
}
return count;
}
void dfs(vector<vector<char>>& grid, int row, int col){
//切记!!遍历过得岛屿不能置为0!!会出错!
//grid[row][col] = '0';
grid[row][col] = '2';
//上
if(row - 1 >= 0 && grid[row-1][col] == '1'){
dfs(grid, row-1, col);
}
//下
if(row + 1 <= grid.size()-1 && grid[row+1][col] == '1'){
dfs(grid, row+1, col);
}
//左
if(col - 1 >= 0 && grid[row][col - 1] == '1'){
dfs(grid, row, col-1);
}
//右
if(col + 1 <= grid[0].size()-1 && grid[row][col + 1] == '1'){
dfs(grid, row, col+1);
}
}重要思路:将水的流向反转,假设太平洋和大西洋的水 从低向高 “攀登”,分别能到达哪些位置,分别用 p_visited 和 a_visited 表示。两者的交集就代表能同时流向太平洋和大西洋的位置。
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
int row = heights.size();
int col = heights[0].size();
vector<vector<bool>> P(row, vector<bool>(col, false));
vector<vector<bool>> A(row, vector<bool>(col, false));
for(int i = 0; i < row; i++){
dfs(heights, P, i , 0);
dfs(heights, A, i, col-1);
}
for(int j = 0; j < col; j++){
dfs(heights, P, 0, j);
dfs(heights, A, row-1, j);
}
vector<vector<int>> res;
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(P[i][j] == true && A[i][j] == true){
vector<int> tmp;
tmp.push_back(i);
tmp.push_back(j);
res.push_back(tmp);
}
}
}
return res;
}
void dfs(vector<vector<int>>& heights, vector<vector<bool>>& ocean, int row, int col){
if(ocean[row][col]){
return;
}
int m = ocean.size();
int n = ocean[0].size();
//上来就置为true是因为在边上的这些雨水自然而然能流到 所以就首先标记一下
ocean[row][col] = true;
//上
if(row >= 1 && heights[row][col] <= heights[row-1][col]){
dfs(heights, ocean, row - 1, col);
}
//下
if(row + 1 <= m - 1 && heights[row][col] <= heights[row+1][col]){
dfs(heights, ocean, row + 1, col);
}
//左
if(col >= 1 && heights[row][col] <= heights[row][col-1]){
dfs(heights, ocean, row, col-1);
}
//右
if(col +1 <= n - 1 && heights[row][col] <= heights[row][col+1]){
dfs(heights, ocean, row, col+1);
}
}这道题比较重要,做这道题的时候发现了dfs可能重复遍历的问题
最开始出现问题一直没找到,代码如下:
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int row = grid.size() ;
int col = grid[0].size();
int max_area = 0;
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
cout<<i<<j<<endl;
dfs(grid, i, j, max_area, 0);
}
}
return max_area;
}
void dfs(vector<vector<int>>& grid, int row, int col, int& max_area, int tmp_area){
if(grid[row][col] == 0){
return;
}
if(tmp_area >= max_area){
max_area = tmp_area;
}
//up
if(row - 1 >= 0 && grid[row - 1][col] == 1){
dfs(grid, row - 1, col, max_area, tmp_area + 1);
}
//down
if(row + 1 <= grid.size() - 1 && grid[row + 1][col] == 1){
dfs(grid, row + 1, col, max_area, tmp_area + 1);
}
//left
if(col - 1 >= 0 && grid[row][col - 1] == 1){
dfs(grid, row, col - 1, max_area, tmp_area + 1);
}
//right
if(col + 1 <= grid[0].size() - 1 && grid[row][col + 1] == 1){
dfs(grid, row, col + 1, max_area, tmp_area + 1);
}
}
};做了这么多道题了,才发现这个问题,就是没有标记,结果他一直会循环的dfs,走过的地方会重新走
借助这一道题,以后这种的要注意了,遍历过后一定要把遍历的值改变
比如这里面,遍历过得岛屿置为0就好
int maxAreaOfIsland(vector<vector<int>>& grid) {
int row = grid.size() ;
int col = grid[0].size();
int max_area = 0;
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(grid[i][j] == 1){
max_area = max(dfs(grid, i, j), max_area);
}
}
}
return max_area;
}
int dfs(vector<vector<int>>& grid, int row, int col){
grid[row][col] = 0;
int count = 1;
//up
if(row - 1 >= 0 && grid[row - 1][col] == 1){
count += dfs(grid, row - 1, col);
}
//down
if(row + 1 <= grid.size() - 1 && grid[row + 1][col] == 1){
count += dfs(grid, row + 1, col);
}
//left
if(col - 1 >= 0 && grid[row][col - 1] == 1){
count += dfs(grid, row, col - 1);
}
//right
if(col + 1 <= grid[0].size() - 1 && grid[row][col + 1] == 1){
count += dfs(grid, row, col + 1);
}
return count;
}难点:如何判断封闭岛屿?其实可以这样想,只要是不封闭的岛屿,必然回合外边界有接触,我们可以这样子去判断
所以代码中表现出来即当岛屿在边界的时候0, row, 0, col时候返回false
int closedIsland(vector<vector<int>>& grid) {
int row = grid.size();
int col = grid[0].size();
int count = 0;
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(grid[i][j] == 0){
if(dfs(grid, i , j)){
count++;
}
}
}
}
return count;
}
bool dfs(vector<vector<int>>& grid, int row, int col){
int m = grid.size();
int n = grid[0].size();
//判断是否在边界
if(row < 0 || row >= m || col < 0 || col >= n ){
return false;
}
//考虑一个0被9个1包围的情况,当碰到一时返回true
if(grid[row][col] == 1){
return true;
}
//走过的路置为1防止重复
grid[row][col] = 1;
//dfs,不用担心越界的问题,因为越界了直接返回false了
bool up = dfs(grid, row-1, col);
bool down = dfs(grid, row + 1, col);
bool left = dfs(grid, row, col - 1);
bool right = dfs(grid, row, col + 1);
return up && down && left && right;
}本质上就是计算岛屿的数量,grid2中的每个岛屿如果都在grid1中,就可以++
所以当grid1[row][col] == 0表明grid2就不是gird1的子岛屿
int countSubIslands(vector<vector<int>>& grid1, vector<vector<int>>& grid2) {
int row = grid2.size();
int col = grid2[0].size();
int count = 0;
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(grid2[i][j] == 1){
bool flag = true;
dfs(grid1, grid2, i, j, flag);
if(flag){
count++;
}
}
}
}
return count;
}
void dfs(vector<vector<int>>& grid1, vector<vector<int>>& grid2, int row, int col, bool& flag){
if(grid2[row][col] == 0){
return;
}
//表明grid2中的岛屿不在grid1中
if(grid1[row][col] == 0){
flag = false;
}
//遍历过得要改掉
grid2[row][col] = 0;
//up
if(row - 1 >= 0 && grid2[row-1][col] == 1){
dfs(grid1, grid2, row-1, col, flag);
}
// down
if(row + 1 <= grid2.size() - 1 && grid2[row+1][col] == 1){
dfs(grid1, grid2, row+1, col, flag);
}
// left
if(col - 1 >= 0 && grid2[row][col-1] == 1){
dfs(grid1, grid2, row, col-1, flag);
}
// right
if(col + 1 <= grid2[0].size() - 1 && grid2[row][col + 1] == 1){
dfs(grid1, grid2, row, col+1, flag);
}
}-
思路
首先是个矩阵,用到了240的思想,找target,看是第几个数,记为m
m和k比较,这就是二分的思想了
-
代码(二分)
int kthSmallest(vector<vector<int>>& matrix, int k) { int row = matrix.size(); int col = matrix[0].size(); int left = matrix[0][0]; int right = matrix[row-1][col-1]; while(left < right){ int target = left + (right - left) / 2; int count = searchMatrix(matrix, target); if(count < k){ left = target + 1; }else{ right = target; } } return right; } int searchMatrix(vector<vector<int>>& matrix, int target){ int row = matrix.size(); int col = matrix[0].size(); int i = 0; int j = col - 1; int count = 0; while(i < row && j >= 0){ if(matrix[i][j] <= target){ i++; count += j + 1; }else{ j--; } } return count; }
-
思路1——二分法
题目要求不能修改数组,不能用额外的存储空间
所以排序再二分是肯定不行了!
那么我们用抽屉原理,从1到数组长度之间求中位数mid,看看mid在给定数组中小于等于mid的有几个,如果正好等于mid,不就表明没有重复嘛
如果大于mid,就表明在1-mid之间肯定有重复的,自己想想就行
其实这道题的巧点在于二分查找的数组可不是原数组,而是1-给定数组长度的这个数组,就是{1、2、3、4、5、...、len}这个数组
为啥能这么做,因为是数字都在
[1, n]范围内 -
思路二——快慢指针
-
代码——二分法
int findDuplicate(vector<int>& nums) { int left = 1; int right = nums.size() - 1; while(left <right){ int mid = left + (right - left) / 2; int count = 0; for(int n : nums){ if(n <= mid){ count++; } } if(count > mid){ right = mid; }else{ left = left + 1; } } return left; }
对一个数组如下:13582353456789来说,我们看一看怎么删除最小的使他有序
因为是一个非递减数组,因此我们可以将数组分成三部分:左边部分,中间部分,右边部分
左边部分是递增的如[1358];中间部分是乱的如[235],右边部分也是递增的如[3456789]
OK那么第一种情况,假如左边部分的最后一个叫做left_end是小于等于右边部分right_start的第一个的话,那么只需要删除中间部分就好了,比如例子1235863456,只需要删除586就可以组合左边部分和右边部分。
第二种情况就是大多数情况,即left_end的值是大于right_start的值的,这个时候我们怎么删除呢?当时做到这点的时候我一直有一个误区,就是以为要把左边部分+中间部分或者中间部分+右边部分全部删除,看谁删除的数量最小就可以了,为啥会用到二分法呢?后来仔细思考了一下不对的,不一定要把左边区间或右边区间全部删除!如下图:
依次查找左边部分的每一个元素在右边部分出现的位置,然后函数中间的这么多元素就可以了。因为这样就不用把左边的全部删除,因为把左边全部删除是错误的思路,左边的一部分可以和右边的有序元素拼接在一起
int findLengthOfShortestSubarray(vector<int>& arr) {
int n = arr.size();
if(n <= 1){
return 0;
}
int left_end = n-1;
int right_start = 0;
for(int i = 1; i < n ; i++){
if(arr[i] < arr[i-1]){
left_end = i;
break;
}
}
for(int i = n - 1; i >= 1; i--){
if(arr[i] < arr[i-1]){
right_start = i;
break;
}
}
if(left_end > right_start){
return 0;
}
//默认最大删除是删除左边+中间
int delete_num = right_start;
//为了更方便表示,left_end是第一个不满足的索引会更好
for(int i = 0; i < left_end; i++){
int index = lower_bound(arr.begin() + right_start, arr.end(), arr[i]) - arr.begin();
delete_num = min(delete_num, index - i - 1);
}
return delete_num;
}切记,如果是严格递归的话,即有重复也不行,就要改left_end和right_start的判断条件,以及用upper_bound来找!阿里的题就是不能有重复数字
这道题的意思就是在数组中查找target
int search(vector<int>& nums, int target) {
int l = 0;
int r = nums.size() - 1;
while(l <= r){
int mid = l+(r-l)/2;
if(nums[mid] == target){
return mid;
}
//先判断nums[mid]和nums[l]的关系,因为你要看是不是在一个有序字序列中
if(nums[mid] >= nums[l]){
//target在nums[l]-nums[mid]
if(target >= nums[l] && target < nums[mid]){
r = mid - 1;
}else{
//target在nums[mid]-nums[r]
l = mid + 1;
}
}else{
//还是target
if(target < nums[mid]){
r = mid - 1;
}
else if(target > nums[mid] && target <= nums[r]){
l = mid + 1;
}else if(target > nums[mid]){
//这种情况被漏掉了导致没做出来
r = mid - 1;
}
}
}
return -1;
}这道题和33相比呢,有个条件变了,数组有重复的值
10111 和 1110111101 这种。此种情况下 nums[start] == nums[mid],分不清到底是前面有序还是后面有序,此时 start++ 即可。相当于去掉一个重复的干扰项。
bool search(vector<int>& nums, int target) {
int l = 0;
int r = nums.size() - 1;
while(l <= r){
int mid = l + (r-l)/2;
if(nums[mid] == target){
return true;
}
//这个if是重点!!!
if(nums[l] == nums[mid]){
l++;
// r--;
continue;
}
if(nums[mid] >= nums[l]){
if(target < nums[mid] && target >= nums[l]){
r = mid - 1;
}else{
l = mid + 1;
}
}else{
//mid < nums[l]
if(target < nums[mid] ){
r = mid - 1;
}
else if(target > nums[r]){
r = mid - 1;
}
else if(target > nums[mid] && target <= nums[r]){
l = mid + 1;
}
}
}
return false;
}首先要注意题目条件,在题目描述中出现了 nums[-1] = nums[n] = -∞,这就代表着 只要数组中存在一个元素比相邻元素大,那么沿着它一定可以找到一个峰值
注意,这道题为什么二分的方向只能是往上爬而不是往下降呢?
因为可以想象成爬山(没错,就是带你去爬山),如果你往下坡方向走,也许可能遇到新的山峰,但是也许是一个一直下降的坡,最后到边界。但是如果你往上坡方向走,就算最后一直上的边界,由于最边界是负无穷,所以就一定能找到山峰,总的一句话,往递增的方向上,二分,一定能找到,往递减的方向只是可能找到,也许没有。
两个问题:①为什么是r<l ②为什么是r=mid,这两个问题看例子[1]和[1,2,1,3,5,6,4]
int findPeakElement(vector<int>& nums) {
int l = 0;
int r = nums.size() - 1;
//注意 不能是l<=r了,要是l<r
while(l < r){
int mid = l + (r-l)/2;
cout<<mid<<endl;
//往上走,mid的右边一定有元素,可以思考一下为什么
if(nums[mid] <= nums[mid + 1]){
l = mid + 1;
}else{
r = mid;
}
}
return l;
}前缀和,用一个数组存前缀和,由于是positive integers nums,所以前缀和这个数组肯定是递增的,所以这个数组可以用来做 二分
时间复杂度是$nlogn$
具体:我们得出了前缀和数组pre_sum,pre_sum[i]表示num[0]-num[i-1]的和
可以想一下,我们有这个前缀和如何找和目标target相关的值呢?我们是需要看前缀和数组中哪两个数相减等于target的,举个例子:
数组[2,3,1,2,4,3]的前缀和为pre_sum[0,2,5,6,8,12,15],target为7,那么我们想找contiguous subarray=7的话就是相减,比如12-5,15-8这样
那么反过来我们计算机的思维就是用target+每一个pre_num[i],看在数组中能不能找到,找到了获得索引,就能知道子数组相加等于target的长度是多少
int minSubArrayLen(int target, vector<int>& nums) {
int res = INT_MAX;
int n = nums.size();
vector<int> pre_sum(n+1, 0);
//前缀和
for(int i = 1; i < n + 1; i++){
pre_sum[i] = pre_sum[i-1] + nums[i-1];
}
//二分,用lower_bound
//一次遍历每个pre_sum
for(int i = 0; i < n+1; i++){
int tmp = target + pre_sum[i];
auto index = lower_bound(pre_sum.begin(), pre_sum.end(), tmp);
if(index != pre_sum.end()){
res = min(res, (int)((index-pre_sum.begin())-i));
}
}
//可能没有等于target的
return res == INT_MAX ? 0 : res;
}+++
-
思路
把数组看做一个指针,比如
[1,2,3,4,5]变成指针就是1→2→3→4→5比如说有数组
[1,2,3,4,5,6,7,8,9,5],那么重复元素就会有循环,即[6 7 8 9] [6 7 8 9] [6 7 8 9],自己手画一下就行了。所以有重复元素的话,就必然会出现一个圈
快慢指针解决掉它
slow = m+p,fast = m+p+q+p 因为fast走一圈相当于slow走两圈,所以有2*slow = fast,可以得到m=q
就表示从0到m和相遇点到到m的距离是一样的。
因为我们这道题求得不是在哪儿相遇的问题,而是形成圆的关键点即重复的数字是哪个,所以要求形成圆的那个点的具体位置
-
代码
int findDuplicate(vector<int>& nums) { int slow = 0; int fast = 0; while(true){ slow = nums[slow]; fast = nums[nums[fast]]; if(slow == fast){ break; } } int begin = 0; int again = slow; while(true){ begin = nums[begin]; again = nums[again]; if(begin == again){ break; } } return begin; }
+++
-
就是加上条件的贪心罢了。
思路是先判断每一行第一列和最后一列的值和目标值的比较,如果在这一行的范围内,就一次匹配就行,或者二分
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int r = matrix.size();
int c = matrix[0]. size();
if(matrix[0][0] > target){
return false;
}
for(int i = 0; i < r; i++){
if(matrix[i][0] <= target && matrix[i][c - 1] >= target){
for(int j = 0; j < c; j++){
if(matrix[i][j] == target){
return true;
}
}
return false;
}
}
return false;
}vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
vector<int> result(n, 0);
for(auto tmp : bookings){
result[tmp[0] -1] += tmp[2];
if(tmp[1] < n){
result[tmp[1]] += -tmp[2];
}
}
for(int i = 1; i < n; i++){
result[i] += result[i-1];
}
return result;
}这道题难理解在于传入参数:
vector<int>& start1: (x1,y1)vector<int>& end1: (x2,y2)vector<int>& start2:(x3,y3)vector<int>& end2:(x4,y4)
有序情况下:
用一个K大小的队列来存储,第k个就是要找的
链表1: 1->2->3->4->5->6->7->8->9
链表2: 2->4->5->7->9->10->11->13->14
求两个链表中第5个值是?
**思路:**有序的思路很简单。首先在两个链表中各维护一个指针,一次往后入队列,第K个就是
无序的情况下:
链表1: 3->9->1->8->7->6->5->4->2
链表2: 9->10->14->7->13->4->11->2->5
求两个链表中第5个值是?
**思路:**建立一个K大小的最大堆,记录最大堆的最大元素。这里面要点就是每次插入元素都能实时排序,自动记录最大元素。然后依次遍历两个链表,将元素一次入堆。如果元素小于最大值,则入堆,最大值会改变。如果元素大于最大值,则继续下一个元素。
"id" : 1, "login":2019-07-25 02:00:00, "logout" : 2019-07-25 04:00:00
"id" : 10, "login":2019-07-25 06:00:00, "logout" : 2019-07-25 08:00:00
"id" : 12, "login":2019-07-25 07:00:00, "logout" : 2019-07-25 08:00:00
给定这么个日志数据,求最大在线峰值人数。
思路:将每个登录时间和登出时间转换成时间戳。时间戳表示对应的秒数,一天有$246060$秒,即有arr[86400]这个数组表示一天中的所有秒数,然后在秒数内的+1,最后扫描一遍整个数组,得到最大值。
转换过后的时间戳如下:
"id" : 1, "login":1563991200, "logout" : 1563998400
"id" : 10, "login":1564005600, "logout" : 1564012800
"id" : 12, "login":1564009200, "logout" : 1564012800再减去2019-07-25 00:00:00得到如下:
"id" : 1, "login":7200, "logout" : 14400
"id" : 10, "login":21600, "logout" : 28800
"id" : 12, "login":25200, "logout" : 28800比如id1中,数组从arr[7200]到arr[14000]都加1,就这样作。
当然上面思路有瑕疵,可以进一步优化。
标准时间格式转换成时间戳:
int standard_to_stamp(char *str_time) { struct tm stm; int iY, iM, iD, iH, iMin, iS; memset(&stm,0,sizeof(stm)); iY = atoi(str_time); iM = atoi(str_time+5); iD = atoi(str_time+8); iH = atoi(str_time+11); iMin = atoi(str_time+14); iS = atoi(str_time+17); stm.tm_year=iY-1900; stm.tm_mon=iM-1; stm.tm_mday=iD; stm.tm_hour=iH; stm.tm_min=iMin; stm.tm_sec=iS; printf("%d-%0d-%0d %0d:%0d:%0d\n", iY, iM, iD, iH, iMin, iS); //标准时间格式例如:2016:08:02 12:12:30 return (int)mktime(&stm); }
相似题目leetcode上1109
**题目描述:**已知一个二维数组 nums ,存储着上下级的关系。其中第一个元素代表员工 employee,第二个元素代表老板 manager。当 manage 为 -1 时,代表没有上级了。最后通过 Json 的格式,输出上下级的关系。
输入:nums = [[1,5],[2,6],[5,6],[6,-1],[4,-1]]
4为胜负手,到最后先手和后手必有一方获胜。n为4的倍数时先手必输。
bool canWinNim(int n) {
return n % 4 != 0;
}bool stoneGame(vector<int>& piles) {
return true;
}小易有 n个数字排成一个环,你能否将它们分成连续的两个部分(即在环上必须连续),使得两部分的和相等?
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int t,n;
const int maxn=1e5+5;
ll a[maxn];
int main(){
cin>>t;
while(t--){
cin>>n;
ll sum=0;
for(int i=0;i<n;i++){
cin>>a[i];
sum+=a[i];
}
// 如果和为奇数,直接判断NO即可
if(sum&1){
cout<<"NO"<<endl;
continue;
}
ll ans = sum/2;
ll res = 0;
int flag = 0;
int i=0,j=0;
while(i<n && j<n){
if(res == ans){
flag=1;
break;
}else if(res<ans){
res+=a[j++];
}else{
res-=a[i++];
}
}
if(flag) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
string replaceSpace(string s) {
string res;
for(auto tmp : s){
if(tmp == ' '){
char tmp1 = '%';
res.push_back(tmp1);
char tmp2 = '2';
res.push_back(tmp2);
char tmp3 = '0';
res.push_back(tmp3);
}else{
res.push_back(tmp);
}
}
return res;
}-
思路一,用一个新空间
string reverseLeftWords(string s, int n) { int len = s.size(); if(len <= 1){ return s; } string res(len, '\0'); int i = n; int j = 0; while(i < len){ res[j] = s[i]; i++; j++; } i = 0; j = len - n; while(i < n){ res[j] = s[i]; i++; j++; } return res; }
-
思路二:将前n个放到后面,删除前n个就行
string reverseLeftWords(string s, int n) { int len_orignal = s.size(); for(int i = 0; i < n; i++){ s.push_back(s[i]); } int len = s.size(); for(int i = 0; i < len - n; i++){ s[i] = s[i+n]; } for(int i = len_orignal; i < len ;i++){ s[i] = '\0'; } return s; }
注意一点就,即s1栈有数据,s2栈有数据的时候,先停止将s1的数据往s2里面倒,先把s2的清空!
class CQueue {
public:
stack<int> s1;
stack<int> s2;
CQueue() {
}
void appendTail(int value) {
s1.push(value);
return;
}
int deleteHead() {
int tmp = 0;
if(!s2.empty()){
tmp = s2.top();
s2.pop();
}
else if(s2.empty() && !s1.empty()){
while(!s1.empty()){
s2.push(s1.top());
s1.pop();
}
tmp = s2.top();
s2.pop();
}else{
return -1;
}
return tmp;
}
};还是得两个栈,一个辅助栈,一个记录数据的栈,辅助栈只记录pop的最小值就行了
public:
/** initialize your data structure here. */
stack<int> s1;
stack<int> s2; //辅助栈
MinStack() {
}
void push(int x) {
s1.push(x);
if(s2.empty()){
s2.push(x);
}else{
int tmp = s2.top() > x ? x : s2.top();
s2.push(tmp);
}
}
void pop() {
if(!s1.empty() && !s2.empty()){
s1.pop();
s2.pop();
}
}
int top() {
if(!s1.empty()){
return s1.top();
}else{
return 0;
}
}
int min() {
return s2.top();
}
};