README.md

1609. Even Odd Tree

A binary tree is named Even-Odd if it meets the following conditions:

• The root of the binary tree is at level index 0, its children are at level index 1, their children are at level index 2, etc.
• For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
• For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).

Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.

Example 1:

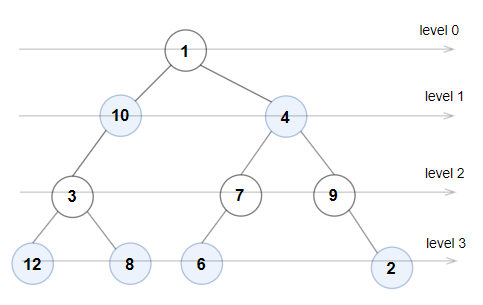
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
Output: true
Explanation: The node values on each level are:
Level 0: [1]
Level 1: [10,4]
Level 2: [3,7,9]
Level 3: [12,8,6,2]
Since levels 0 and 2 are all odd and increasing, and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.

Example 2:

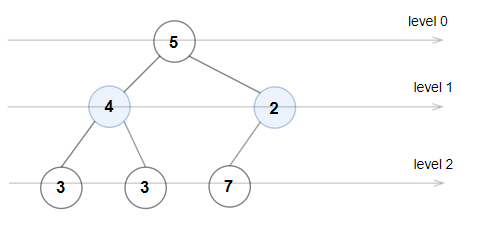
Input: root = [5,4,2,3,3,7]
Output: false
Explanation: The node values on each level are:
Level 0: [5]
Level 1: [4,2]
Level 2: [3,3,7]
Node values in the level 2 must be in strictly increasing order, so the tree is not Even-Odd.

Example 3:

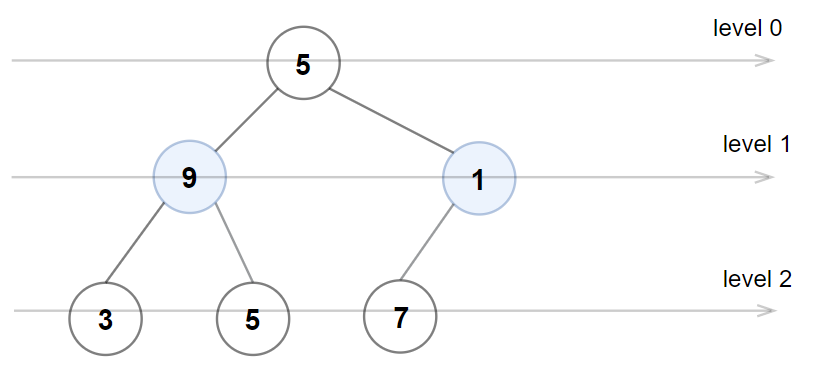
Input: root = [5,9,1,3,5,7]
Output: false
Explanation: Node values in the level 1 should be even integers.

Example 4:

Input: root = [1]
Output: true

Example 5:

Input: root = [11,8,6,1,3,9,11,30,20,18,16,12,10,4,2,17]
Output: true

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 106

Solutions (Python)

1. Level Order Traversal

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isEvenOddTree(self, root: TreeNode) -> bool:
        even_index = True
        curr_level = [root]

        while curr_level != []:
            prev_val = 0 if even_index else 1_000_001
            next_level = []

            for node in curr_level:
                if (even_index and
                    (node.val % 2 == 0 or prev_val >= node.val)) or \
                        (not even_index and
                         (node.val % 2 == 1 or prev_val <= node.val)):
                    return False

                prev_val = node.val
                if node.left is not None:
                    next_level.append(node.left)
                if node.right is not None:
                    next_level.append(node.right)

            even_index = not even_index
            curr_level = next_level

        return True

Solutions (Ruby)

1. Level Order Traversal

# Definition for a binary tree node.
# class TreeNode
#     attr_accessor :val, :left, :right
#     def initialize(val = 0, left = nil, right = nil)
#         @val = val
#         @left = left
#         @right = right
#     end
# end
# @param {TreeNode} root
# @return {Boolean}
def is_even_odd_tree(root)
  even_index = true
  curr_level = [root]

  until curr_level.empty?
    prev_val = even_index ? 0 : 1_000_001
    next_level = []

    curr_level.each do |node|
      return false if even_index && (node.val.even? || prev_val >= node.val)
      return false if !even_index && (node.val.odd? || prev_val <= node.val)

      prev_val = node.val
      next_level.push(node.left) unless node.left.nil?
      next_level.push(node.right) unless node.right.nil?
    end

    even_index = !even_index
    curr_level = next_level
  end

  true
end