一元函数:一个自变量输入为$x$,一个因变量输出为$y$。
多元函数:多个自变量输入为$x, y$,一个因变量输出为$y$。
为了我们能够在多个变量的函数中考虑只有一个自变量变化的变化率,我们需要定义一个叫做偏导数的概念。
定义 设函数$z=f(x, y)$在点$(x_0, y_0)$的某领域内有定义,将$y$固定为$y_0$,而$x$在$x_0$处取得增量$\Delta x$ 时,$f(x, y)$所产生的相应增量:
称为$f(x, y)$关于$x$的偏增量,如果极限:
存在,则称此极限为函数$z=f(x, y)$在点$(x_0, y_0)$处对$x$的偏导数,记做:
也就是: $$f'x(x_0, y_0) = \lim{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{ \Delta x}$$
同理,可以得到函数$f(x, y)$对$y$的偏导数: $$f'y(x_0, y_0) = \lim{\Delta y \to 0} \frac{f(y_0 + \Delta y) - f(y_0)}{ \Delta y}$$
如果函数$z=f(x, y)$在区域$D$内每一点$(x,y)$都有对$x$的偏导数$f'_x(x,y)$或对$y$的偏导数$f'_y(x,y)$,且$f'_x(x,y)$和$f'_y(x,y)$仍是$x,y$的函数,我们将其偏导函数(简称偏导数),可以记做:
偏导数的定义可以推广到三元以上函数的情形。根据偏导数的定义,当多元函数表达式已经给出的时候,求他的各个偏导数并不需要新方法,将其他变量固定为常量,对单个变量利用一元函数求导方法求导即可
举例
求$z=5x_0^2 + x_0x_1$在点$(x_0=1,x_1=2)$处的偏导数.
先将$x_1$看作常量,对$x_0$求导得到:
将$x_0$看成常量,对$x_1$求导得到:
于是带入$x_0=1, x_1 = 2$到上式中得到:
推广到向量
在章节1.1中我们谈到:将多个标量放在一起可以形成向量。那么,我们重新从向量角度重新看一眼偏导数。我们将$N$个自变量放到一起可以组成一个向量$X=[x_0, x_1,..., x_N]$,输出得到一个标量$y$。于是我们的函数$f(X), \mathbb R^N \to \mathbb R$ 输入是一个向量(多个自变量),输出是一个标量。于是,在任意一点$X \in \mathbb R$,
复合函数的偏导数
对于一元函数,我们可以使用链式法则对复合函数进行求导。对于多元函数,由于复合函数的构成可以更加复杂,因此无法针对所有情况给出通用的求导公式,但是可以针对其中一种情况给出求导公式,方便大家发现读者发现其中的求导规律。
定理1 如果函数$u=\varphi(x, y), v=\psi(x, y)$ 在点$(x,y)$的各偏导数都存在,$z=f(u, v)在对应点$(u,v)可微,则复合函数$z=f(\varphi(x,y), \psi(x,y))$在点$(x, y)$的偏导数存在,且
举例
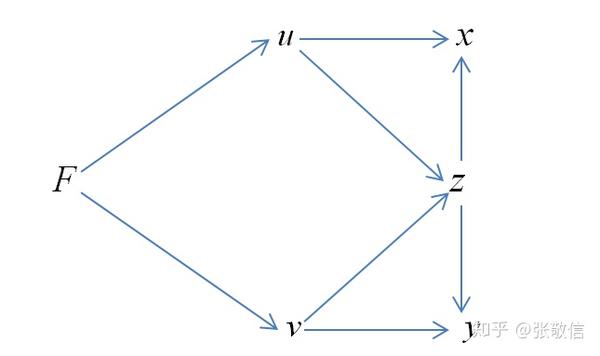
假设函数$F(x,y,z) = xz + yz,令u(x,z) = xz, v(y,z)=yz,F(u,v) = u + v$那么$F,u,v,x,y,z)之间的计算关系可以如图2.4.1所示,结构图2.4.1显示$z$不仅和u相关,也和v相关,于是我们试着计算一下偏导数