До сих пор я говорил об одиночных IP, путешествующих по сетям, как автомобили и автобусы в системе автомагистралей. Говорил, как потоки IP можно рассматривать как объекты более высокого уровня и как им, в свою очередь, можно придать более сложную структуру с помощью «скобочных» IP. Надеюсь, я показал, что с помощью этих концепций можно легко обрабатывать довольно сложные приложения.
Но что если мы хотим построить ещё более сложные структуры и перемещать их по сети как отдельные элементы? Потокам требуется время, чтобы пересечь соединение, и вы можете захотеть, чтобы вся структура данных была отправлена или получена в один момент времени. Как мы уже говорили, по сети перемещаются только дескрипторы, а для IP, содержащего один бит, перемещаться от процесса к процессу так же легко, как и для IP, содержащего мегабайт. Так почему бы не позволить сложным структурам перемещаться как единицам? Оказалось, что у этой идеи есть естественный аналог в реальной жизни (которая всегда убеждает нас в том, что мы на правильном пути!). Ранее мы упоминали идею, что IP похожи на заметки — вы можете избавиться от них одним из трех способов: вы можете переслать их (send), отбросить (drop) или сохранить (используя различные методы, например, стек, сохранение на диск и проч.). Ну, и, конечно же, есть четвертое, что вы можете сделать с запиской (нет, не скомкать ее и не швырнуть в соседа) - прикрепить ее к другому листу бумаги, а затем сделать с полученным результатом одно из трех предыдущих действий. На самом деле вы можете прикрепить такую "составную заметку" к другому листу бумаги или к другой составной заметке и так далее.
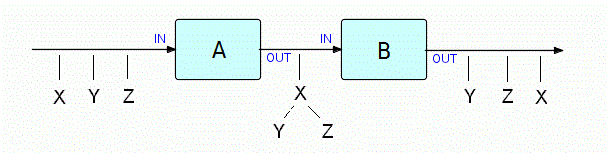
Подобно тому, как составное сообщение может быть отправлено или получено как единое целое, так и структура связанных IP, называемая деревом, может быть отправлена или получена как единый объект. Как только процесс получил дерево, он может либо «пройтись» по нему (перейти от IP к IP по связующим звеньям), полностью либо частично разобрать его, либо уничтожить. Например, получатель может пройтись по дереву в поисках IP определенного типа, и отсоединить каждый найденный одним из стандартных способов. На следующей диаграмме показаны два процесса: один — сборка деревьев, а другой — их повторная разборка:
Фрагмент 12.1
A преобразует серию из трех IP разных типов и размеров в дерево IP, а B разбирает деревья и выводит IP-компоненты (в другом порядке).
Во всех реализациях этой концепции ни один узел не мог происходить от более чем одного родительского узла, и мы не допускали никаких циклов — очень похоже на настоящее живое дерево! Я не думаю, что при этом мы потеряли много выразительной силы. Основная причина тут в том, чтобы разрешить работу правил владения и распоряжения FBP для IP.
Вы, наверное, уже поняли, что нам не нужны никакие специальные механизмы, покуда дерево собирается и разбирается за одну активацию одного процесса (активация подробно описана в главе о правилах планирования). На самом деле вы можете прочитать набор IP и построить массив указателей для сортировки - так работает ряд компонентов. Только когда дерево должно быть передано от одной активации к другой (от одного процесса к другому), необходимо учитывать правила расположения IP. Таким образом, на картинке выше процесс A получает (или создает) три IP, собирает их в одно дерево из 3 IP и отправляет их — в этом случае A начинает с «количества принадлежащих IP», равного 3, и постепенно уменьшает его до 0, сперва присоединив 2 IP к корню (счетчик теперь равен 1), а затем отправив дерево целиком (счетчик 1 становится равным 0). B получает один IP (счетчик идет от 0 до 1) и отсоединяет подключенные IP (счетчик идет от 1 до 3). Эти отсоединенные IP, конечно, должны быть утилизированы по обычным правилам. Если бы мы допустили какие-либо нарушения вышеприведенных правил о форме дерева, мы не смогли бы так легко отображать деревья и потоки.
Был поразительный пример того, насколько полезными могут быть деревья в FBP: в пакетном банковском приложении банковские счета были представлены сложными последовательными структурами на ленте. Каждая запись счёта состояла из заголовка аккаунта, за которым следовало переменное количество различных записей "хвоста", принадлежащих к большому количеству различных типов - остановки, удержания, элементов возврата и т.д. Проблема заключалась в том, что в большинстве случаев их можно было просто обрабатывать последовательно, но иногда обработка последующих элементов потока приводила к изменениям, которые должны были отражаться в более ранних. Например, для расчета процентов, инициированного определенным типом заключительной записи, может потребоваться обновление баланса счета в записи заголовка. Вы всегда можете сохранить заголовок и вставить его позже, но тогда он должен будет вернуться в правильное положение. Так или иначе, этого «прямого» доступа было довольно много, включая добавление и удаление записей хвостов. Используя обычное программирование, мы сделали это приложение чертовски сложным, ибо вся логика должна была быть скоординирована с точки зрения времени, и возникали временные конфликты между тем, когда что-то требовалось и когда оно становилось доступным! Речь шла о больших объемах таких структур — мы должны были иметь возможность обрабатывать около 5 000 000 каждую ночь. Когда взялись за дело с помощью FBP, то поняли, что можем решить эту задачу очень просто и естественно, преобразовав каждую последовательную запись в древовидную структуру. После того, как дерево было построено, обработка типа «прямой доступ» могла переходить от одного типа IP к другому в структуре дерева, добавлять или удалять IP и т.д. А затем все это можно было преобразовать обратно в линейную форму, когда мы закончим. Это решение оказалось простым для понимания, легко кодируемым и простым в обслуживании.
Теперь нарисуем простое дерево из четырех IP:
Фрагмент 12.2
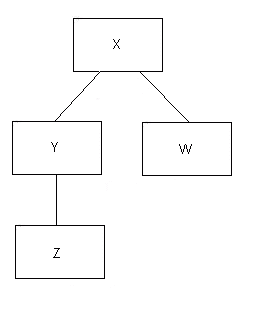
Верхнее поле представляет «корневой» IP, а все остальные IP прямо или косвенно происходят от него. На приведенной выше диаграмме (немного смешивая наши метафоры):
Хэто кореньYиWдочериXZ- дочьYZиW— листья (терминальные IP)Y— нетерминальный IP
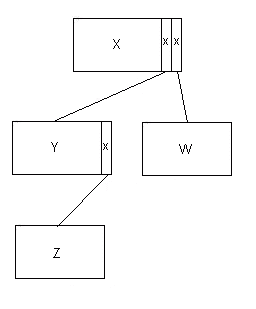
В AMPS и более ранних версиях DFDM использовался подход, где для подключенного IP требовалось указать поле указателя как часть материнских данных. Это означало, что древовидную структуру можно было пройти только с использованием языков, поддерживающих указатели, например, PL/I, C и т.д. Но у него было то преимущество, что при использовании этих языков нам не нужно было иметь никаких явных сервисов обхода дерева. На самом деле нам нужны были только сервис «присоединить» и «отсоединить». Более фундаментальная проблема заключалась в том, что формат данного IP должен был учитывать максимальное количество дочерних элементов, которое он мог иметь, поэтому на приведенной выше диаграмме X должен был предоставить (как минимум) два указателя, а Y — один. Схематично (с указателями, обозначенными крестиками):
Фрагмент 12.3
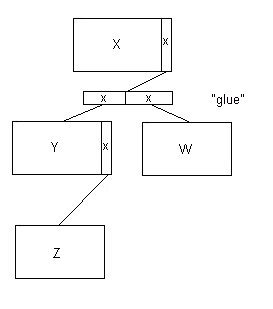
Однако, если бы Y и W можно было представить как единый список (а не как два разных вида отношений) — скажем, детей сотрудника, — вы могли бы создать «склеивающие» IP и использовать их для наблюдения за связью. Приведенная выше диаграмма тогда будет выглядеть так:
Фрагмент 12.4
Этот простой механизм позволяет создавать самые разнообразные структуры, создавая специальные типы IP, которые содержат различные схемы указателей. Например, вы можете построить цепочку, просто добавив одно поле указателя к каждому IP в цепочке, которое можно использовать для последующего IP, если он есть. Вы можете создавать списки, подобные LISP, используя указатели «car» и «cdr» для каждого IP или даже только для определенных зарезервированных типов IP («клея»). Мой коллега Чарльз Дуглас придумал изящную аналогию: когда вы используете скрепку для скрепления двух заметок, скрепка занимает некоторое место на бумаге!
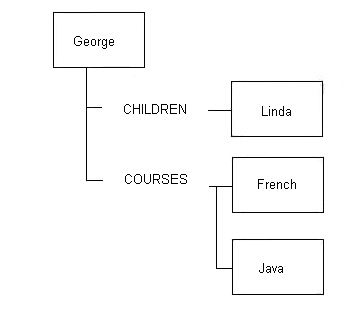
Что касается японского продукта DFDM, наша группа считает, что вам не нужно заранее планировать все структуры списков, которые могут быть связаны с IP. Например, к сотруднику могут быть прикреплены списки с указанием детей, посещенных курсов, отделов, в которых он работал, история заработной платы и т.д. И было бы очень хорошо, если бы эту информацию можно было добавлять постепенно, без необходимости изменять описания участвующих IP. Поэтому мы ввели идею именованных цепочек, любое количество которых может быть добавлено к IP без необходимости каких-либо изменений в описании этого IP. Например, к IP сотрудника могут быть прикреплены следующие цепочки: CHILDREN, SALARY_HIST, COURSES и т.д. Затем нам, конечно, нужно предоставить сервисы обхода. Мы фактически создали несколько довольно мощных служб, например, "добавить IP в именованную цепочку" (он создается, если еще не существует), получить следующую цепочку (чтобы можно было пройтись по цепочкам, не зная их имен), получить первый IP именованной цепочки, получить следующий IP в цепочке, отсоединить IP от цепочки и т.д. Вы можете привязать цепочку к IP или IP к цепочке, но не цепочку к цепочке или IP к IP. Таким образом, эти деревья имели менее однородную структуру (цепочки, чередующиеся с IP данных), но мы чувствовали, что это по-прежнему обеспечивает мощную парадигму и менее «зависимый от программиста» подход к манипулированию деревьями и обходу. ИП сотрудника с одним ребенком Линдой, прошедшим два курса, может выглядеть так:
Фрагмент 12.5
Аналогично, как и при явном удалении IP, нам пришлось наложить определенные ограничения на то, как деревья могут быть разложены. На это намекали выше, когда мы говорили о «прямом» и «косвенном» владении. Кореневой IP принадлежит непосредственно тому процессу, который только что его получил. Таким образом, IP, которые связаны с этим корнем, косвенно принадлежат одному и тому же процессу (они не принадлежат никому напрямую, кроме, возможно, корневого IP). Вы можете отправить или удалить только тот IP, которым владеете напрямую. Сначала вам нужно отсоединить связанный IP, а затем отправить или удалить его. Однако процесс может привязать другой IP (которым он должен владеть напрямую) к IP, которым он владеет только косвенно, но это всё, что он может с ним сделать не считая, разве что, просто чтения! Мы также добавили логику для проверки, что процесс не пытался связать корневой IP с одним из своих потомков — это было бы разрешено другими правилами, но привело бы к замкнутому циклу!
Если вышеизложенное звучит сложно, попробуйте следующую аналогию: предположим, вы только что срубили дерево и хотите избавиться от него. Кажется разумным, что прежде чем сжечь ветку, ее нужно сначала отрезать. Мы могли бы устроить так, что сжигание ветки без предварительного ее отрезания «прижгло бы» место прикрепления, но кажется, что это добавило бы ненужной сложности. И наоборот, мы разрешим вам добавлять листья и ветки к дереву, но только если они не связаны с другим деревом! Также нельзя прикреплять предметы к дереву таким образом, чтобы часть дерева превратилась в замкнутый круг!
Еще один момент, связанный с деревьями, заключается в том, что иерархические древовидные структуры, независимо от того, как они реализованы, могут быть легко преобразованы во вложенные подпотоки, подобные описанным в главе 11. Например, дерево, показанное на рис. 12.2, можно преобразовать в линейную форму следующим образом:
<X <Y Z> W>
Фрагмент 12.6
Где соглашение заключается в том, что IP, следующий за левой скобкой, является «матерью» других IP на том же уровне вложенности скобки. Этот вид преобразования будет знаком пользователям LISP. На самом деле мы только что показали «список списков» LISP.
В описанной выше реализации «цепочки» нам пришлось бы собирать идентификаторы цепочки, поэтому мы можем просто добавить информацию о цепочке в левые скобки, как мы делали это в главе 9. Таким образом, после приведения к линейной форме дерево, показанное на рис. 12.5, могло бы выглядеть следующим образом (как и в предыдущих главах, «имя группы» отображается как часть данных IP в открытых и закрытых скобках):
IP type data
< employees
employee George
< children
child Linda
> children
< courses
course French
course COBOL
> courses
> employees
Фрагмент 12.7
Затем его можно легко преобразовать обратно в древовидный формат, если это необходимо. Это также, конечно, очень хорошо соответствует различным подходам к базам данных: «дети» и «курсы» могут быть разными типами сегментов в базе данных IBM DL/I. В IBM DB2 мы могли бы создать разные таблицы employee, children и courses, где employee — это первичный ключ таблицы employee и внешний ключ (foreign key) двух других. [Конечно, это прекрасно отображается в XML!]
И последнее замечание: хотя мы несколько раз заявляли, что считаем, что IP должны удаляться явно, оказалось очень полезно иметь возможность отбрасывать все дерево за раз. Таким образом, дерево должно иметь достаточно внутренних «лесов», чтобы сервис «отбрасывания» мог найти все цепочки и подключенные IP и отбросить их. Более поздние версии DFDM в любом случае нуждались в этом, чтобы предоставлять такие функции, как «найти следующую цепочку», но эта возможность удалить целое дерево оказалась важной, даже когда у нас не было сервисов обхода. Хотя сначала казалось, что приложения всегда будут знать о древовидной структуре достаточно, чтобы выполнять свою работу самостоятельно, мы разрабатывали все больше и больше общих компонентов, которые понимали деревья в целом, но не конкретные древовидные структуры. Это средство, возможно, больше всего напоминает средство "сборки мусора" в объектно-ориентированных и списко-ориентированных языках.