Spectro started with the goal of building a music visualiser after being inspired from some of the cool WebGL experiments over on Shadertoy. Having recently started a new job at Atlassian as a frontend developer, I was looking for a fun project that would help me brush up on my web skills after my last mostly backend job in C#/.NET. Some long weekends later (and some weeknights too...) Spectro was born, and although I didn't end up achieving my initial goal I still managed to build something I think is as equally cool and fun to play around with.
So what is Spectro? The title explains it all really – it's a real-time spectrogram generator for the web that can visualize audio directly from your microphone or any other input device exposed by your browser. It also supports generating spectrograms from audio files on your device, and has a bunch of parameters to control the appearance of the spectrogram in real-time.
If you've never seen a spectrogram before, they look something like this:

Spectrogram of some opera generated in Spectro
A spectrogram is essentially a visualization of the different frequencies present in some audio, with time represented along the horizontal axis and frequency along the vertical axis. The intensity of a given frequency at a given point in time is represented by the color of the spectrogram at that point. Spectrograms have a number of applications from visualizing seismic activity to speech recognition in machine learning, although here I've just aimed to provide an interesting and fun way of visualizing sound.
When we normally think about sound, we imagine an oscillating wave that changes in shape over time. In computing, we represent sound waves by sampling them at fixed time intervals (usually 44100 Hz) and then store each of these samples as a number between -1.0 and 1.0 in sequential order. When it comes time to play the audio back, these digitized audio samples are sent to a DAC chip which reconstructs the analog signal the samples represent.
Audio represented this way is considered to be in the time-domain, as the audio signal is stored over time. This is normally a great way to think about audio as it's easy to understand and implement, however it doesn't serve us well when we need to know information about the frequencies in the audio. For this we need to be able to convert sound into the frequency-domain, which we can do with a fast Fourier transform (FFT).
A FFT takes samples in the time-domain as input, and gives back complex numbers describing the phases and amplitudes of the different sinusoidal frequencies that make up the input. In effect, this converts a signal over time into phase and amplitude over frequency. This process can be reversed to get back the original signal, and we can even modify parts of the audio in the frequency-domain before converting back, forming the basis of how a lot of digital signal processing works.
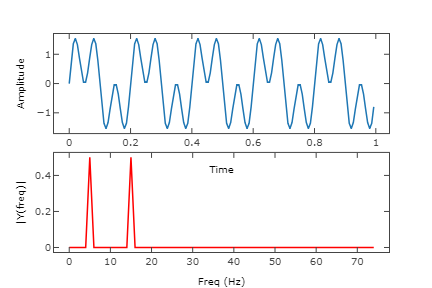
Example of a FFT (bottom, showing amplitude only) applied to a signal with 2 overlapping sinusoidal frequencies (top)
Image credit: @akshaysin
One important thing to note about a FFT is the size of its output: for n samples we get back n frequency bins. In other words: the longer the piece of audio, the more detailed information we have about its frequencies. This is very similar to Heisenberg's uncertainty principle in quantum physics, which states that neither the position nor momentum of a particle can be simultaneously measured with accuracy: only one or the other can be known with any certainty at a given point in time. In the case of a FFT, we can either chop the audio signal up into small chunks to loosely know frequency information at specific points in time, or use the entire audio signal to precisely know frequency information without knowing exactly when different frequencies occur.
When generating a spectrogram this property is very important, as it means we can have high resolution on one axis or the other, but not both. For Spectro I decided to break the audio signal up into blocks of 4096 samples (about 90ms at 44100 Hz) which I thought provided a good balance between time and frequency resolution. 4096 samples gives us a resolution in the vertical axis of 2048 pixels which is about the height of a 4K display, and 90ms resolution in the time axis is well below the length of most musical notes.
Now you might be a bit confused around how 4096 audio samples only gives us a frequency resolution of 2048 – after all wouldn't we have 4096 frequency bins to display? This is because the second half of a FFT is actually a 90-degree phase shifted mirror of the first half when the input samples are all real numbers, as is the case with audio. This is to do with the fact that a FFT actually deals with complex sinusoidal waves, so when we provide it with samples that only describe a real sinusoidal wave we end up with a complex wave made from two identical yet orthogonal real waves. Since we don't care about the same information twice, we only actually have n / 2 frequency bins worth of information to display. This answer on StackExchange explains it in much more detail if you're interested!
So we know that we can break an audio signal up into small chunks, perform a FFT on each chunk, and get information about the frequencies in each chunk. Surely that's all we need to do before we can start displaying that data on the screen to create our spectrogram? Not quite – we haven't talked about windowing yet.
A FFT assumes that the samples you provide are part of an infinitely repeating wave. You've probably heard that sound your computer makes when it glitches out and plays the same few milliseconds of audio over and over, causing an awful piercing sound. This sounds bad for a reason: each time the audio repeats it creates very high frequencies when the last audio sample suddenly wraps back to the first with no transition. This is what a FFT thinks is happening when you pass it a small chunk of audio that's been cut out, causing the frequency-domain data to be polluted with a bunch of frequencies that aren't actually in the audio.

What happens when you don't use a windowing function, note all of the vertical lines
To fix this, we use what's called a windowing function. This essentially fades out the samples of the audio chunk towards each end to create a smoother transition between repeating instances of the chunk. To window a chunk, we simply multiply each sample by the corresponding value on the window function which usually has a bell-like shape.
While a windowing function significantly reduces the amount of pollution we get in the frequency-domain (more commonly referred to as side-lobes), it doesn't eliminate them completely. Different windowing functions have different effects on side-lobes, although generally the more you reduce the side-lobes the narrower your window needs to be, reducing the amount of samples you have to analyse.
A Blackman-Harris window function (left) and its effect on the corresponding FFT (right), note the low side-lobe intensity in the frequency-domain
For Spectro I decided on a Blackman–Harris window due to its minimal side-lobes. To compensate for narrowness of the window, Spectro computes the FFT for each 4096 sample window every 1024 samples. While overlapping the windows this way means we have to compute the FFT for the same sample 4 times, it ensures that every sample is more fairly represented in the final spectrogram. Without overlapping in this way, samples that lie towards the edge of each chunk wouldn't get taken into consideration in the spectrogram due to the windowing function mapping them to near zero.
Now time for the fun part: taking our windowed audio data converted to the frequency-domain and displaying it on the screen. In an early prototype of Spectro I was using a plain old canvas, manually mapping each window of FFT data to a vertical line of colors and writing them to pixels on the screen. Surprisingly this approach actually was pretty fast – I could easily get 60fps in real-time using a microphone as my audio source. It probably helped that I was performing all the CPU intensive work such as computing the FFT and doing the color mapping in a dedicated web worker, but performance definitely wasn't a huge issue using this method.
The biggest problem with software rendering however was performance when I wanted to go back and re-render existing parts of the spectrogram. Let's say that we wanted to zoom in on the spectrogram, make it brighter, or switch to a different color scheme. This would require re-drawing the entire spectrogram, which turns out to be a very slow process when you have a screen full of pixels to update on the CPU.
While I could have accepted it as a limitation that it would take some time to update any of the drawing parameters, I didn't think this would have made for a very fun experience. If only computers had some way of updating millions of pixels simultaneously... oh wait they do! This was the perfect time to get the GPU involved to do all the heavy lifting using WebGL.
My first task was to get all of the raw FFT data (specifically, the amplitudes of each frequency bin) onto the GPU for rendering. Given that Spectro just displays the most recently recorded audio in a scrolling fashion, I needed to keep the last X FFT windows in memory (where X is the width of the canvas) while also allowing for very fast updates as audio came in. This was a perfect task for a circular queue, which uses a fixed size array to store data while keeping track of start and end pointers as data is added and removed. Every time a new audio window is ready it is processed and added to the queue, possibly overwriting the oldest data in the queue, with the WebGL renderer checking the queue each frame for new data to display. When new data is found it gets copied to a single-channel floating-point texture on the GPU, which is designed to be eventually consistent with the FFT data found in the queue. Since only new data is written to the texture each frame the update is very fast, achieved using a call to texSubImage2D().
Now that the GPU was being fed a stream of FFT data, I needed to map it to pixels on the screen. For this I started by rendering a fullscreen rectangle, using a very simple fragment shader to display the FFT texture on the rectangle in black and white. This was a good start, but the spectrogram would just stay in the same place on the screen while updating from left to right as the circular queue was written to. This wasn't the effect I was going for, as I wanted the screen to scroll with the most recent audio data to appearing on the right and least recent on the left.
To implement this, I started passing the start and end pointers of the circular queue to the fragment shader. These values were then used to apply a transformation to the texture coordinates when sampling the FFT texture so that the start pointer always appeared on the left, and the end pointer appeared on the right. One limitation with this approach was that it meant we had to sample past the end of the texture: when we apply an offset along the x-axis we eventually reach the rightmost edge of the texture and need to start displaying pixels from the leftmost edge again. Normally we can tell WebGL to automatically handle wrapping texture coordinates for us by setting the TEXTURE_WRAP_* texture parameters to REPEAT, however this is only supported for textures that have dimensions that are a power of two. Given that our FFT texture has a width equal to the canvas width, this wasn't an option.

Non power of two textures in WebGL have their texture coordinates always clamped to the edge
At this point I was worried that what I was trying to achieve wouldn't be feasible, however I realised that there was a very simple solution that could be implemented in the shader: the mod() function. We can apply our transformations to the texture coordinate and then take its modulo with 1.0 to ensure that the coordinate is always wrapped in the range of 0.0 to 1.0. This approach does mean that we lose smooth interpolation between the first and last row of pixels in the FFT texture, but the effect is hardly noticeable given that the spectrogram is normally viewed at full resolution rather than being extremely zoomed in.
The only thing left to do now was implement some options to control the appearance of the spectrogram. Some were trivial to implement and just involved a simple mathematical operation with the FFT data on the shader, like multiplication in the case of the sensitivity option. Others like the frequency scale and color scheme took a bit more effort.
To implement colorization, so that the spectrogram would show color for different frequency intensities rather than black and white, I used a fairly common technique where a color gradient is uploaded to the GPU as a single dimensional texture. We can then sample this texture at a position from 0.0 to 1.0 to get the corresponding color for a given value. In the case of the spectrogram, we sample the color ramp at a position equal to the value of the FFT amplitude at a given point. To make the transition between different colors a bit smoother, I decided to use quadratic interpolation between each color in the gradient along with interpolating in the Lab color space. Using quadratic interpolation helped to add some smoothness, while using Lab color helped to make the transition between different colors appear a bit more natural. Switching between different color schemes is then as simple as regenerating the color ramp texture and uploading it to the GPU.

One of the color ramp textures, using quadratic interpolation in the Lab color space
I used a similar technique for implementing the frequency scale option, which makes different frequencies appear larger or smaller in the spectrogram along the y-axis. The two options I implemented are linear, which performs no scaling, and Mel which is designed to closely model how we perceive pitch by giving more weight to lower frequencies. We can implement different scales by again using a texture – for a given position in the texture we get back a value that tells us where in the FFT data we should sample from. For the linear scale this increases from 0.0 to 1.0, well, linearly, while for Mel it increases much slower at the start before speeding up towards the end based on the formula for the Mel scale.

Scale textures for Mel (top) and linear (bottom)
There were a lot of other implementation details that I didn't cover here to keep the focus on the interesting bits, but I hope I've been able to provide some insight into digital signal processing and displaying real-time heat map data using WebGL.
Spectro is fully open source, so feel free to look into anything I didn't cover yourself or play around the code to build something completely new!