-
Notifications
You must be signed in to change notification settings - Fork 768
Synchronization, Part 8: Ring Buffer Example
A ring buffer is a simple, usually fixed-sized, storage mechanism where contiguous memory is treated as if it is circular, and two index counters keep track of the current beginning and end of the queue. As array indexing is not circular, the index counters must wrap around to zero when moved past the end of the array.
As data is added (enqueued) to the front of the queue or removed (dequeued) from tail of the queue, the current items in the buffer form a train that appears to circle the track
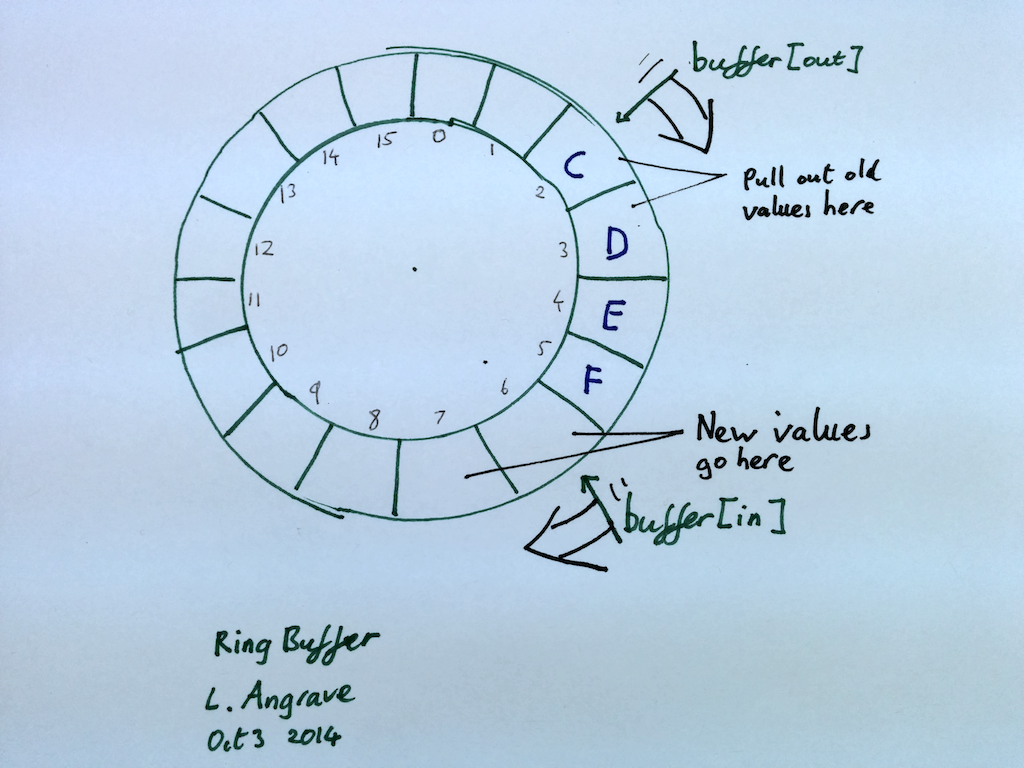 A simple (single-threaded) implementation is shown below. Note enqueue and dequeue do not guard against underflow or overflow - it's possible to add an item when when the queue is full and possible to remove an item when the queue is empty. For example if we added 20 integers (1,2,3...) to the queue and did not dequeue any items then values
A simple (single-threaded) implementation is shown below. Note enqueue and dequeue do not guard against underflow or overflow - it's possible to add an item when when the queue is full and possible to remove an item when the queue is empty. For example if we added 20 integers (1,2,3...) to the queue and did not dequeue any items then values 17,18,19,20 would overwrite the 1,2,3,4. We won't fix this problem right now, instead when we create the multi-threaded version we will ensure enqueue-ing and dequeue-ing threads are blocked while the ring buffer is full or empty respectively.
void *buffer[16];
int in = 0, out = 0;
void enqueue(void *value) { /* Add one item to the front of the queue*/
buffer[in] = value;
in++; /* Advance the index for next time */
if (in == 16) in = 0; /* Wrap around! */
}
void *dequeue() { /* Remove one item to the end of the queue.*/
void *result = buffer[out];
out++;
if (out == 16) out = 0;
return result;
}It's very tempting to write the enqueue or dequeue method in the following compact form (N is the capacity of the buffer e.g. 16):
void enqueue(void *value)
b[ (in++) % N ] = value;
}This method would appear to work (pass simple tests etc) but contains a subtle bug. With enough enqueue operations (a bit more than two billion) the int value of in will overflow and become negative! The modulo (or 'remainder') operator % preserves the sign. Thus you might end up writing into b[-14] for example!
A compact form is correct uses bit masking provided N is 2^x (16,32,64,...)
b[ (in++) & (N-1) ] = value;This buffer does not yet prevent buffer underflow or overflow. For that, we'll turn to our multi-threaded attempt that will block a thread until there is space or there is at least one item to remove.
The following code is an incorrect implementation. What will happen? Will enqueue and/or dequeue block? Is mutual exclusion satisfied? Can the buffer underflow? Can the buffer overflow?
For clarity pthread_mutex is shortened to p_m and we assume sem_wait cannot be interrupted.
#define N 16
void *b[N]
int in = 0, out = 0
p_m_t lock
sem_t s1,s2
void init() {
p_m_init(&lock, NULL)
sem_init(&s1, 0, 16)
sem_init(&s2, 0, 0)
}
enqueue(void *value) {
p_m_lock(&lock)
// Hint: Wait while zero. Decrement and return
sem_wait( &s1 )
b[ (in++) & (N-1) ] = value
// Hint: Increment. Will wake up a waiting thread
sem_post(&s1)
p_m_unlock(&lock)
}
void *dequeue(){
p_m_lock(&lock)
sem_wait(&s2)
void *result = b[(out++) & (N-1) ]
sem_post(&s2)
p_m_unlock(&lock)
return result
}Before reading on, see how many mistakes you can find. Then determine what would happen if threads called the enqueue and dequeue methods.
- The enqueue method waits and posts on the same semaphore (s1) and similarly with equeue and (s2) i.e. we decrement the value and then immediately increment the value, so by the end of the function the semaphore value is unchanged!
- The initial value of s1 is 16, so the semaphore will never be reduced to zero - enqueue will not block if the ring buffer is full - so overflow is possible.
- The initial value of s2 is zero, so calls to dequeue will always block and never return!
- The order of mutex lock and sem_wait will need to be swapped (however this example is so broken that this bug has no effect!)
The following code is an incorrect implementation. What will happen? Will enqueue and/or dequeue block? Is mutual exclusion satisfied? Can the buffer underflow? Can the buffer overflow?
For clarity pthread_mutex is shortened to p_m and we assume sem_wait cannot be interrupted.
void *b[16]
int in = 0, out = 0
p_m_t lock
sem_t s1, s2
void init() {
sem_init(&s1,0,16)
sem_init(&s2,0,0)
}
enqueue(void *value){
sem_wait(&s2)
p_m_lock(&lock)
b[ (in++) & (N-1) ] = value
p_m_unlock(&lock)
sem_post(&s1)
}
void *dequeue(){
sem_wait(&s1)
p_m_lock(&lock)
void *result = b[(out++) & 15]
p_m_unlock(&lock)
sem_post(&s2)
return result;
}- The initial value of s2 is 0. Thus enqueue will block on the first call to sem_wait even though the buffer is empty!
- The initial value of s1 is 16. Thus dequeue will not block on the first call to sem_wait even though the buffer is empty - oops Underflow! The dequeue method will return invalid data.
- The code does not satisfy Mutual Exclusion; two threads can modify
inoroutat the same time! The code appears to use mutex lock. Unfortunately the lock was never initialized withpthread_mutex_init()orPTHREAD_MUTEX_INITIALIZER- so the lock may not work (pthread_mutex_lockmay simply do nothing)
The pseudo-code (pthread_mutex shortened to p_m etc) is shown below.
As the mutex lock is stored in global (static) memory it can be initialized with PTHREAD_MUTEX_INITIALIZER.If we had allocated space for the mutex on the heap, then we would have used pthread_mutex_init(ptr, NULL)
#include <pthread.h>
#include <semaphore.h>
// N must be 2^i
#define N (16)
void *b[N]
int in = 0, out = 0
p_m_t lock = PTHREAD_MUTEX_INITIALIZER
sem_t countsem, spacesem
void init() {
sem_init(&countsem, 0, 0)
sem_init(&spacesem, 0, 16)
}The enqueue method is shown below. Notice:
- The lock is only held during the critical section (access to the data structure).
- A complete implementation would need to guard against early returns from
sem_waitdue to POSIX signals.
enqueue(void *value){
// wait if there is no space left:
sem_wait( &spacesem )
p_m_lock(&lock)
b[ (in++) & (N-1) ] = value
p_m_unlock(&lock)
// increment the count of the number of items
sem_post(&countsem)
}The dequeue implementation is shown below. Notice the symmetry of the synchronization calls to enqueue. In both cases the functions first wait if the count of spaces or count of items is zero.
void *dequeue(){
// Wait if there are no items in the buffer
sem_wait(&countsem)
p_m_lock(&lock)
void *result = b[(out++) & (N-1)]
p_m_unlock(&lock)
// Increment the count of the number of spaces
sem_post(&spacesem)
return result
}- What would happen if the order of
pthread_mutex_unlockandsem_postcalls were swapped? - What would happen if the order of
sem_waitandpthread_mutex_lockcalls were swapped?
Legal and Licensing information: Unless otherwise specified, submitted content to the wiki must be original work (including text, java code, and media) and you provide this material under a Creative Commons License. If you are not the copyright holder, please give proper attribution and credit to existing content and ensure that you have license to include the materials.