读《算法图解》— 对算法的一些基本理解

[Val-Zhang]

「算法」二字听来高深，常常让人望而却步，而《算法图解》是一本对算法初学者友好的书，此书图文并茂，循序渐进的帮我们理清算法中一些基础概念，还介绍了一些有意思的算法及其用途，以提升读者的兴趣，帮助我们步入算法的大门。本书也许不仅仅是一本讲述概念的书，作者还在潜移默化中培养我们的算法思维，从计算机的角度来看待问题。

原书中的示例使用 Python 编写，不过考虑到目前我日常工作中使用最多的还是JavaScript，为了加深自己对相关概念的理解，笔记中我又用 JS 重写了一些示例。

何为算法

算法其实没有那么高深，它只是一组完成任务的指令。任何代码片段都可以视为算法。
算法又没有那么简单，虽然写出来的完成任务的代码都是算法，但是算法也有好坏之分。

算法为何重要

选用合适的算法能大大缩短运算时间。

关于这点，我们来看一个实际的例子。

问题：
从 1 ~ 100 个数中猜出某个我现在想到的数字，我只会告诉你「大了」，「小了」，「对了」，最快需要几次猜到？

解决这个问题有多种方案，如果你运气好，也许1次就猜对了，运气差也许会需要100次。有一种叫做「二分查找」的算法非常适合解决这类问题。

二分查找

定义：
二分查找是一种算法，其输入是一个有序的元素列表，如果元素包含在列表中，二分查找返回其位置，否则返回 null.

分析：
简单查找模式：从1开始往上猜，又称「傻找」，最多会需要99次猜测。
二分查找：每次猜最大，最小数字的中间值，由此每次可排除一般的可能性，最多只需要7次就可猜对。

一般而言，对于包含n个元素的列表，用二分查找最多需要 ㏒₂n步，而简单查找最多需要n步。

代码实现

/* 二分查找 */
function binarySearch(arr = [], item) {
  let low = 0,
    high = arr.length - 1;
  while (low <= high) {
    const mid = parseInt((low + high) / 2);
    const guess = arr[mid];
    if (guess === item) {
      return mid;
    }
    if (guess > item) {
      high = mid - 1;
    }
    if (guess < item) {
      low = mid + 1;
    }
  }
  return null;
}

const myList = [1, 3, 5, 7, 9];
console.log(binarySearch(myList, 3));
console.log(binarySearch(myList, 10));

上面提到简单查找模式最多需要 99 次猜测， 而用二分查找最多需要 ㏒ n步，这其实引出了另外一个算法初学者还不算熟悉但很重要的概念 — 运行时间。

算法速度的表征方式 —— 大O表示法

我们都想选用效率最高的算法，以最大限度的减少运行时间或占用空间，换句话说我们想要选用时间复杂度低的算法，大O表示法是一种指明算法的速度有多快的特殊表示法，常常用它来表示时间复杂度。我们继续以上面的例子来说明
比如说我们 1ms 能查看一个元素，下表表现了不同元素个数简单查找和二分查找找到某个元素的时间

不要误解，大O表示法并非指的是以秒为单位的速度，而是告诉我们运行时间会以何种方式随着运算量的增加而增长，换句话说它指出了算法运行时间的的增速。

例如,假设列表包含 n 个元素。简单查找需要检查每个元素,因此需要执行 n 次操作。使用大O表示法, 这个运行时间为O(n)。O 是 Operation 的简写。

还需要注意的是大O表示法指出的是最糟糕的情况下的运行时间，这种运行时间是一个保证。

一些常见的时间复杂度

算法的时间复杂度往往是以下几种中的一种或者组合，虽然还没有介绍到具体的算法，不过我们可以先就各种时间复杂度留下一个印象。

• O(log n):也叫对数时间，这样的算法包括二分查找；
• O(n):也叫线性时间，这样的算法包括简单查找；
• O(n * log n): 这种算法包括快速排序 —— 一种速度较快的排序算法；
• O(n²):这样的算法包括选择排序 —— 一种速度较慢的排序算法；
• O(n!): 这样的算法包括难以解决的旅行商问题 —— 一种非常慢的算法。

算法常常和数据结构挂钩。在介绍数据结构之前，我们需要先理解内存的工作原理，这样有助于我们理解数据结构。

常见的数据结构 — 数组和链表

内存的工作原理

我们可以把计算机的内存想象成有很多抽屉的柜子，每个柜子都有其编号。

当需要将数据存储到内存时，我们会请求计算机提供存储空间，计算机会分配一个柜子给我们（存储地址），一个柜子只能存放一样东西，当需要存储多项连续的数据时，我们需要以一种特殊的方法来请求存储空间，这就涉及到两种基本的数据结构—数组和链表。

数组和链表的区别

数组

「数组」这个概念我们很熟悉，在我们的平日的开发过程中会经常用到，不过暂时忘记 JavaScript 中的 Array 吧。我们来看看数组的本质。

使用数组意味着所有的存储事项在内存中都是相连的。
这样做的优点是，如果我们知道某个存储事项的索引，我们只需要一步就能找到其对应的内容。
但是缺点也显而易见，如果计算机开始为我们的数组分配的是一块只能容纳三项的空间，当需要存储第四项的时候，会需要把所有内容整体移动到新的分配区域。如果新的区域再满了，则需要再整体移动到另外一个更大的空区域。因此有时候在数组中添加新元素是很麻烦的一件事情。针对这个问题常见的解决方案时预留空间，不过预留空间也有两个问题：
* 可能浪费空间；
* 预留的空间可能依旧不够用；

链表

链表中的元素可以存储在任何地方，链表的每个元素都存储了下一个元素的地址，从而使得一系列的内存地址串在一起。

我们可以通过一个更形象的比如来理解链表，可以把链表比作一个寻宝游戏，前往某个地点后，会打开一个宝箱，其中有一张纸条上写着下个地点的位置。

考虑到链表的这些性质，链表在「插入元素」方便颇具优势，存储后只需要修改相关元素的指向内存地址即可。当然伴随而来也有劣势，那就是在需要读取链表的最后一个元素时，必须从第一个元素开始查找直至找到最后一个元素。

链表的劣势恰恰是数组的优势，当需要随机读取元素时，数组的效率很高。（数组中的元素存储的内存地址相邻，可容易计算出任意位置的元素的存储位置）。

链表和数组各种操作的时间复杂度对比

操作	数组	链表
读取	O(1)	O(n)
插入	O(n)	O(1)
删除	O(n)	O(1)

删除只考虑删除，不考虑读取，由于数组支持随机访问，而数组支持随机访问，因此数组用得多。

前面介绍的「二分查找」的前提是查找的内容是有序的，在熟悉了数组和链表后，我们来学习第一种排序算法—选择排序。

选择排序

定义
遍历一个列表，每次找出其中最大的那个值，存入一个新的列表，并从原来的列表中去除该值，直到排完。

时间复杂度
每次遍历的时间复杂度为O(n),需要执行n次，因此总时间为O(n²)。

虽然需要遍历的个数越来越少，平均检查元素数为½*n，但是大O表示法常常忽略常数。

示例代码

function findSmallest(arr) {
  let smallest = arr[0];
  let smallest_index = 0;
  for (let i = 1; i < arr.length; i++) {
    if (arr[i] < smallest) {
      smallest = arr[i];
      smallest_index = i;
    }
  }
  return smallest_index;
}

function selectionSort(arr) {
  const newArr = [];
  const length = arr.length;
  for (let i = 0; i < length; i++) {
    const smallestIndex = findSmallest(arr);
    debugger
    newArr.push(arr.splice(smallestIndex, 1)[0]);
    debugger;
  }
  return newArr;
}

console.log(selectionSort([5, 7, 3, 6, 1, 8]));  /* [ 1, 3, 5, 6, 7, 8 ]*/

附：我们可以在VisuAlgo - Sorting (Bubble, Selection, Insertion, Merge, Quick, Counting, Radix)查看选择排序的动态过程。

上面的选择排序用到了循环，递归是很多算法都使用的一种编程方法，甚至不夸张的讲，递归是一种计算机思维。

递归

递归是一种优雅的问题解决方法。其优雅体现在它让解决方案更为清晰，虽然在性能上，有些情况下递归不如循环。

如果使用循环，程序的性能可能更高；如果使用递归，程序可能更容易理解。 —- Leigh Caldwell

递归的组成

递归由两部分组成：

• 基线条件（base case）：函数不再调用自己的条件
• 递归条件（recursive case）: 函数调用自己的条件

上面提到，递归可能存在性能问题，想要理解这一点，需要先理解什么是「调用栈」。

「栈」是一种先入后出（FILO）简单的数据结构。「调用栈」是计算机在内部使用的栈。当调用一个函数时，计算机会把函数调用所涉及到的所有变量都存在内存中。如果函数中继续调用函数，计算机会为第二个函数页分配内存并存在第一个函数上方。当第二个函数执行完时，会再回到第一个函数的内存处。

我们再看看「递归调用栈」：

使用递归很方便，但是也要̶出代价：存储详尽的信息需要占用大量的内存。递归中函数会嵌套执行多层函数，每个函数调用都要占用一定的内存，如果栈很高，计算机就需要存储大量函数调用的信息，这就是为什么有的语言会限制递归最多的层数。

如果所有函数都是尾调用，那么完全可以做到每次执行时，调用记录只有一项，这将大大节省内存。这就是"尾调用优化"的意义。

附：栈和堆的区别
尾调用优化

上面提到的 「选择排序」还是太慢，接下来我们基于递归介绍一种业界通用的排序方法 —— 快速排序。

在正式讲解「快速排序」之前，我们先介绍一下「分而治之」这种方法。
「分而治之 」（divide and conquer D&C ）是一种著名的递归式问题解决方法。只能解决一种问题的算法毕竟作用有限，D&C 可能帮我们找到解决问题的思路。

分而治之

运用 D & C 解决问题的过程包括两个步骤：

1. 找出基线条件，这种条件必须尽可能简单；
2. 不断将问题分解，直到符合基线条件；（每次递归调用都必须缩小问题的规模）

我们以快速排序为例来看看，如何运用分而治之的思维。

快速排序

1. 选择基准值
2. 将数组分为两个子数组，小于基准值的元素和大于基准值的元素
3. 对两个子数组再次运用快速排序

代码实现

const quickSort = (array) => {
  if (array.length < 2) {
    return array;
  }
  const pivot = array[0];
  const keysAreLessPivot = array.slice(1).filter(key => key <= pivot);
  const keysAreMorePivot = array.slice(1).filter(key => key > pivot);
  return [...quickSort(keysAreLessPivot), pivot, ...quickSort(keysAreMorePivot)];
};

console.log(quickSort([10, 5, 2, 3])); // [2, 3, 5, 10]

在最糟情况下，栈长为 O(n)，而在最佳情况下，栈长为O(log n)。
快速排序的平均时间复杂度为 nlog(n)，比选择排序快多了O(n²)。

常见的数据结构 —— 散列表

在编程语言中，存在另外一种和数组不同的复杂数据结构，比如JavaScript中的对象，或 Python 中的 字典。对应到计算机的存储上，它们可能可以对应为 散列表。

要理解散列表，我们需要先看看散列函数。

散列函数

散列函数是一种将输入映射到数字，且满足以下条件的函数：

• 相同的输入会得到相同的输出；
• 不同的输入会映射到不同的数字

散列函数准确的指出了数据的存储位置，能做到这个是因为：

• 散列函数总是将同样的输入映射到相同的索引；
• 散列函数将不同的输入映射到不同的索引；
• 散列函数知道数组有多大，只返回有效的索引；

我们可以把散列表定义为::使用散列函数和数组创建了一种数据结构。::

散列表也被称为 「散列映射」，「映射」，「字典」和「关联数组」。

但是就像上面提到的，需要连续内存位置的数组存储空间毕竟有限，散列表中如果两个键映射到了同一个位置，一般做法是在这个位置上存储一个链表。

散列表的用途

由于散列函数的存在，散列表中数据的查找变得非常快，散列函数值唯一，本身就是一种映射，基于这些，散列表可用作以下用途：

• 模拟映射关系
• 防止重复
• 缓存/记住数据

使用散列表页存在一些注意事项：

1. 散列函数很重要，理想的情况下，散列函数将键均匀地映射到散列表的不同位置；
2. 如果散列表存储的链表很长，散列表的速度将急剧下降；

散列表的时间复杂度

理想情况下 散列表的操作为O(1)，但是最糟情况下，所有操作的运行时间为O(n)

操作	散列表（平均情况）	散列表最差情况	数组	链表
查找	O(1)	O(n)	O(1)	O(n)
插入	O(1)	O(n)	O(n)	O(1)
删除	O(1)	O(n)	O(n)	O(1)

在平均情况下，散列表的查找速度和数组一样快，而插入和删除速度和链表一样快，因此它兼具二者的优点。但是在最糟的情况下，散列表的各项操作速度都很慢。

要想让散列表尽可能的快，需要避免冲突。
想要避免冲突，需要满足以下两个条件：

• 较低的填充因子；
• 良好的散列函数；

填装因子 = 散列表包含的元素总数 / 位置总数

如果填装因子大于1 意味着商品数量超过数组的位置数。一旦填装因子开始增大，就需要在散列表中添加位置，这被称为调整长度。

一个不错的经验是，当填装因子大于 0.7 的时候，就调整散列表的长度。

良好的散列函数

良好的散列函数让数组中的值呈均匀分布，不过我们不用担心该如何才能构造好的散列函数，著名的SHA 函数，就可用作散列函数。

在大多数编程语言中，散列表都有内置的实现。下面我们看看散列表的用途。

广度优先搜索

广度优先算法是图算法的一种，可用来找出两样东西之间的最短距离。在介绍这种算法之前，我们先看看什么叫图。

什么是图

图由节点（node）和边（edge）组成，它模拟一组连接。一个节点可能与众多节点直接相连，这些节点被称为邻居。有向图指的是节点之间单向连接，无向图指的是节点直接双向连接。

在编程语言中，我们可以用散列表来抽象表示图

广度优先搜索解决的问题

广度优先搜索用以回答两类问题：

• 从节点A出发，有前往节点B的路径吗？
• 从节点A出发，到节点B的哪条路径最短？

我们还是举例来说明该如何运用 广度优先搜索。

芒果销售商问题
如果你想从你的朋友或者有朋友的朋友中找到一位芒果销售商，涉及关系最短的路径是什么呢？

分析：查看自己的朋友中，是否有芒果销售商，如果没有则检查朋友的朋友，在最近的那一层检查完之前不去检查下一层。

编码实现

const graph = {};
graph.you = ['alice', 'bob', 'claire'];
graph.bob = ['anuj', 'peggy'];
graph.alice = ['peggy'];
graph.claire = ['thom', 'jonny'];
graph.anuj = [];
graph.peggy = [];
graph.thom = [];

const isSeller = name => name[name.length - 1] === 'm';

const search = (name, graph) => {
  const iter = (waited, visited) => {
    if (waited.length === 0) {
      return false;
    }
    const [current, ...rest] = waited;
    if (visited.has(current)) {
      return iter(rest, visited);
    }
    if (isSeller(current)) {
      console.log(`${current} is a mango seller!`);
      return true;
    }
    visited.add(current);
    const personFriends = graph[current];
    return iter([...rest, ...personFriends], visited);
  };
  return iter(graph[name], new Set());
};

search('you');

上面的编码中涉及到了一种新的数据结构 —— 队列。

队列
队列的工作原理和现实生活中的队列完全相同，可类比为在公交车前排队，队列只支持两种操作：入队 和 出队。
队列是一种先进先出的（FIFO）数据结构。

散列表模拟图
散列表是一种用来模拟图的数据结构

广度优先算法的时间复杂度

广度优先算法的时间复杂度为 O(V+E) 其中V为顶点数，E为边数。

树

提到图就不得不说一种特殊的图 —— 树。

树其实可以看做是所有的边都只能往下指的图。树的用途非常广，还有很多种分支，更多信息可参考

狄克斯特拉算法

广度优先搜索只能找出最短的路径，但是它却并不一定是最快的路径，想要得到最快的路径需要用到狄克斯特拉算法（Dijkstra’s algorithm）

在狄克斯特拉算法算法中，每段路径存在权重，狄克斯特拉算法算法的作用是找出的是总权重最小的路径。

平时我们使用地图软件导航到某个我们不熟悉的地点时，地图软件往往会给我们指出多条路线。直达但是绕圈的公交并不一定会比需要换乘的地铁快。

狄克斯特拉算法的使用步骤如下：

1. 画一张表，列出所有节点，并标注出从当前出发可到达节点的值，找出其中最便宜（可最快到达）的节点供第二步使用；
2. 更新该节点的到达其所有邻居节点的时间，依据结构修改上面列出的表，检查是否有前往它们的更短路径，如果有，更新其开销，并更新其父节点；
3. 重复这个过程，直到对图中的节点都这么做了；
4. 统计最终的表格，找出最短的路径；

狄克斯特拉算法涉及到的这种拥有权重的图被称为 「加权图」
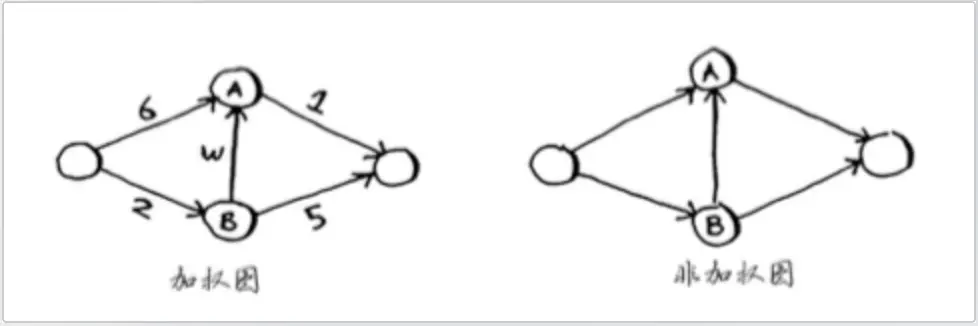
不存在权限的图被称为「非加权图」。

狄克斯特拉算法算法只适用于有向无环图。
不能将狄克斯特拉算法算法用于负权边的情况。

编码实现

// the graph
const graph = {};
graph.start = {};
graph.start.a = 6;
graph.start.b = 2;

graph.a = {};
graph.a.fin = 1;

graph.b = {};
graph.b.a = 3;
graph.b.fin = 5;

graph.fin = {};

// The costs table
const costs = {};
costs.a = 6;
costs.b = 2;
costs.fin = Infinity;

// the parents table
const parents = {};
parents.a = 'start';
parents.b = 'start';
parents.fin = null;

let processed = [];


const findLowestCostNode = (itCosts) => {
  let lowestCost = Infinity;
  let lowestCostNode = null;

  Object.keys(itCosts).forEach((node) => {
    const cost = itCosts[node];
    // If it's the lowest cost so far and hasn't been processed yet...
    if (cost < lowestCost && (processed.indexOf(node) === -1)) {
      // ... set it as the new lowest-cost node.
      lowestCost = cost;
      lowestCostNode = node;
    }
  });
  return lowestCostNode;
};

let node = findLowestCostNode(costs);

while (node !== null) {
  const cost = costs[node];
  // Go through all the neighbors of this node
  const neighbors = graph[node];
  Object.keys(neighbors).forEach((n) => {
    const newCost = cost + neighbors[n];
    // If it's cheaper to get to this neighbor by going through this node
    if (costs[n] > newCost) {
      // ... update the cost for this node
      costs[n] = newCost;
      // This node becomes the new parent for this neighbor.
      parents[n] = node;
    }
  });

  // Mark the node as processed
  processed = processed.concat(node);

  // Find the next node to process, and loop
  node = findLowestCostNode(costs);
}

console.log('Cost from the start to each node:');
console.log(costs); // { a: 5, b: 2, fin: 6 }

并非所有问题都存在最优解

有些时候，我们很难找出最优解，这时候我们可以采用另外一种计算机思维来解决问题 —— 贪婪算法。
贪婪算法指的是每步都采取最优的做法，每步都选择局部最优解，最终的结果一定不会太差。

完美是优秀的敌人。有时候，你只需要找一个能够大致解决问题的算法，此时贪婪算法正好可派上用场，它们的实现很容易，得到的结果又与正确结果接近。这时候采用的算法又被称作近似算法。

判断近似算法优劣的标准如下：

• 速度有多快；
• 得到的近似解和最优解的接近程度；

有的问题也许不存在所谓的最优解决方案，这类问题被称为「NP完全问题」。这类问题以难解著称，如旅行商问题和集合覆盖问题。很多非常聪明的人都认为，根本不可能编写出可快速解决这些问题的算法。对这类问题采用近似算法是很好的方案，能合理的识别NP完全问题，可以帮我们不再无结果的问题上浪费太多时间。

如何识别NP完全问题

以下是NP完成问题的一些特点，可以帮我我们识别NP完全问题：

• 元素较少时，算法的运行速度非常快，但是随着元素的增加，速度会变得非常慢；
• 涉及 所有组合 的问题通常是NP完成问题；
• 不能将问题分解为小问题，必须考虑各种可能的情况的问题，可能是NP完全问题；
• 如果问题涉及到序列且难以解决（旅行商问题中的城市序列），则可能是NP完全问题；
• 如果问题涉及到集合（如广播台集合）且难以解决，可能是NP完全问题；
• 如果问题可转换我集合覆盖问题或者旅行商问题，一定就是NP完全问题；

动态规划

还有一种被称作「动态规划」的思维方式可以帮我们解决问题
这种思维方式的核心在于，先解决子问题，再逐步解决大问题。这也导致「动态规划」思想适用于子问题都是离散的，即不依赖其他子问题的问题。

动态规划使用小贴士：

• 每种动态规划解决方案都设计网格；
• 单元格中的值通常是要优化的值；
• 每个单元格都是一个子问题

附：什么是动态规划？动态规划的意义是什么？—知乎讨论

K最近邻算法

本书对 KNN 也做了简单的介绍，KNN的合并观点如下

• KNN 用于分类和回归，需要考虑最近的邻居。
• 分类就是编组
• 回归就是预测结果
• 特征抽离意味着将物品转换为一系列可比较的数字。
• 能否挑选合适的特征事关KNN算法的成败

进一步的学习建议

读完本书，对算法总算有了一个入门的理解，当然算法还有很多值得深入学习的地方，以下是作者推荐的一些方向。

• 树
• 反向索引：搜索引擎的原理
• 傅里叶变换：傅里叶变换非常适合用于处理信号，可使用它来压缩音乐；
• 并行算法：速度提升并非线性的，并行性管理开销，负载均衡
• MapReduce：是一种流行的分布式算法，可通过流行的开源工具 Apache Hadoop 来使用；
• 布隆过滤器和 HyperLogLog：面对海量数据，找到键对于的值是一个挑战性的事情，布隆过滤器是一种概率性的数据结构，答案可能不对也可能是正确的；其优点在于占用的存储空间很小
• SHA 算法（secure hash algorithm）安全散列函数，可用于对比文件，检查密码
• 局部敏感的散列算法，让攻击者无法通过比较散列值是否类似来破解密码
• Diffie-Hellman 密钥交换
• 线性规划：用于在给定约束条件下最大限度的改善制定的指标

书读完了

《算法图解》确实是一本比较好的算法入门书，不枯燥，又能让人有收获就能激励出人的学习欲望，学习算法单阅读本书肯定还是不够的，

Coursera | Online Courses From Top Universities. Join for Free是一门非常好的算法课，如果感兴趣可以一起学学。