Quantifying long-term scientific impact

[chengjun]

如何衡量论文长期影响力？

读者可能记得，上一期妙算复杂文章我们介绍了颠覆性指数Disruption来量化文章的创新性，它对于跨学科的论文评价尤其适用。但本文列出的综述文章，其价值主要不在于创新性，而在于梳理和总结相关主题的研究脉络和最新动向，并对领域发展提供前瞻性的意见。此时基于引用量刻画这类论文的影响力仍然是主要的方法。

不过，直接使用引用量评价论文（或期刊）的影响力存在着诸多问题：如论文发表时间有先后导致不能公正比较；又如现有的引用数（尤其是短期引用数，如3或5年）并不总能代表其长期影响；再比如期刊影响因子（IF）是基于论文引用量计算的，但是同一刊物同期发表的两篇文章，其引用量常常差别非常大。

有没有一种更合理的评价方案呢？大家可能注意到了，在上一节中我们不是按照引用量，而是按照最终引用量对论文进行排序，就是采用了集智科学家王大顺、网络科学家 Barabási 等2013年在 Science 杂志[4]提出的方法，来衡量论文的长期影响力。下面将具体论述如何创建这样一个指标。

首先，相对于引用数量，引用模式或许可以给我们更多的信息。关于引用模式一个著名的结果是，不同学科的论文，其引用量分布（被引用一定次数的文章占学科内所有文章的比重）经过合适的缩放（rescaling）后服从统一的规律[5]。那么对单篇论文而言，其引用量有无演化规律可循，使我们能根据引用历史预测长期影响呢？

事实上，三大因素主导了单篇论文的引用模式：

• 偏好依附（preferred attachment）：较高引用的文章具有较大的概率被再次引用，这很好地解释了先发优势。偏好依附也是无标度网络的度形成幂律分布的一种方式。
• 老化（aging）：论文的新颖性随着时间推移而衰减。通常而言，在需要引用某主题的文章时，学者们常常引用最新研究，因为这些代表最前沿的进展。
• 适应性（fitness）：论文内在的创新性和重要性，适应性越高，论文被引用的概率越大。

结合这三个因素，我们可以将论文发表 t 时间后被引用的概率表示为三个因子的乘积，经过数学变换可以进一步得到论文 i 在发表 t 时间后的累计引用量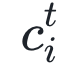的表达式：

其中λi刻画论文适应性的影响，μi, σi刻画老化效应的影响。Φ(x)是正态分布的累积分布函数，m是常量。给定一组数据 t 和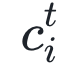，我们可以通过曲线拟合计算出最佳的λi, μi, σi，确定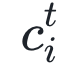的表达式。然后代入不同的 t，就可以计算任意给定年份论文i的累计引用量。

至此，我们就有了预测论文长期引用量的方法。再进一步对引用量 c 和时间 t 做归一化，即滤除偏好依附、老化、适应性三大因素的影响，可以更直观地看到，归一化的论文引用量与时间呈现通用的累积正态分布关系，用曲线表示如下：

论文长期影响指标

当我们得到拟合曲线后，可以计算论文的几个特征指标。我们用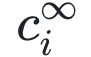表示当 t 趋向于无穷大时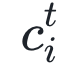的值，也就是论文 i 的最终引用量，其表达式为

也就是说，尽管偏好依附和老化效应在短期内对论文的引用量有显著影响，但长期来看论文的最终引用量仅取决于论文适应性。因此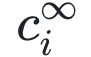可以用来比较不同时期发表的论文的长期影响力。

另一个指标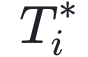表示论文引用量达到几何平均数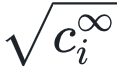（）所用的特征时间，它反应了论文早期引用量的增长速率

可见这一特征时间主要取决于参数μi，而与λi, σi无关。

*三、集智斑图实践*

集智斑图是集智俱乐部创建的复杂科学内容聚合平台，包含了复杂科学最新论文、多领域学习路径、论文解读活动、自组织社区等模块。现在我们将论文长期影响力的预测方法应用到集智斑图的论文中。

对于每一篇论文 ，我们使用历史引用记录拟合参数，并计算论文的最终引用量，下面以排名第8位的论文 p: Vital nodes identification in complex networks 为例进行说明：

(1) 获取 p 发表后每年的引用数据

p 发表于2016年，2016-2021的引用量为: [8,75,123,155,166,132]

（ 数据来源于semantic scholar）

(2) 计算 p 的累计引用数据

2016-2021年的累积引用量为: [8,83,206,361,527,659]

(3) 拟合曲线①，计算出λ, μ, σ

拟合曲线可以使用python中的科学计算程序包scipy，其中的curve_fit函数可以用来做曲线拟合，默认使用的拟合方法是最小二乘法，计算得到的系数(mean ± std)为

λ= 4.06±0.07， μ=0.90±0.01，σ=0.79±0.04

(4) 计算最终引用量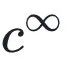

预测的λ=4.06，该文章当前的引用数量为600+，但是预测的长期引用量到达了1100+，说明该文章本身的质量很高，尽管发表了5年仍然有较大的被引潜力。

我们画出 p 引用的实际值和预测值，可以见到本方法在有数据记录的时间段，仅使用λ, μ, σ三个参数取得了很好的拟合效果。同时本方法预测 p 在未来数年内仍有较大幅度的引用增长，之后才趋于稳定。

在我们选出的前10篇文章中，同样也有这样的例子，即长期引用量远大于当前引用，如排名第4的 Continuous-time quantum walks: Models for coherent transport on complex networks 和排名第10的 The physics of communicability in complex networks。这是因为它们的论文质量较高（λ分别为3.75和5.43），达到引用概率峰值的时间较长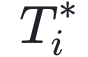（分别为5.25年和14年）。尤其是后面这篇，与大部分文章的引用量集中在发表后的3-5年相比，这篇文章明显例外。在发表近10年后，它的引用量不但没有减少，而且呈现加速上升的趋势，使得拟合的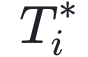达到了14年，长期引用量达到了4000+。这个预测是否准确呢，让我们拭目以待。

用同样的方法可以估计其它论文的长期引用量。需要注意的是，拟合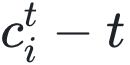曲线至少需要3个数据点，因此对于2020年及以后的论文，无法得到有效的预测值。这种情况我们做简单的处理：计算其他文章最终引用量与前两年引用量的平均比值，并假定这个比值适用于2020以后的论文，由此得到最终的引用量。

import pylab as plt
from scipy.optimize import curve_fit
import numpy as np
from scipy.stats import norm

# demo data
x = np.arange(2016,2021+1)
y =[8,75,123,155,166,132]

x = np.arange(1,len(x)+1)
y_cumsum = np.cumsum(y)

# fit function
##  M measures the average number of references each new paper contains

M = 20

def fi(x):
    return norm.cdf(x)

def func(x,lam,u,sigma):
    return M*(np.exp(lam*fi((np.log(x) - u)/sigma))-1)

def infinite_citation(lam):
    return M*(np.exp(lam) - 1)

#Fits the functions using curve_fit
coes,cov = curve_fit(func,x,y_cumsum)
print("lambda,mu,sigma:",coes)

# plot
plt.figure(figsize=(9,6))
X = np.arange(1,50)

plt.plot(x,y_cumsum,'o',label='Data')
plt.plot(X,func(X,coes[0],coes[1],coes[2]),alpha=0.5,label='Prediction')
plt.xlabel('Year',fontsize=15)
plt.ylabel('Citation',fontsize=15)
plt.legend(fontsize=15)
plt.show()

lambda,mu,sigma: [4.06184015 0.90469353 0.79326431]

代码实现 https://github.com/socrateslab/longterm_citation/blob/main/longterm_citation.ipynb

*四、总结*

本文是妙算复杂栏目第二篇文章，本文第一部分我们基于论文过滤算法，选出了Physics Reports中与网络科学相关的综述合集，并从数据分析的视角做了排序和简单评述。第二部分依据网络科学家 Barabási、集智科学家王大顺等人的算法，基于偏好依附、老化效应和论文适应性等三大因素，预测论文的长期影响力，并将这一算法应用在集智斑图实践中。

网络科学是一门充满魅力的学科，自上世纪末兴起以来吸引了众多研究者投身该领域。集智网络科学第三期课程指出：网络科学第一个十年，重点研究了网络的基本模型及其性质；网络科学第二个十年，重点转入了网络动力学的全面研究，以及网络动力学与网络结构相互关系的探索；网络科学第三个十年，高阶相互作用动力学将引起人们的极大兴趣。本文的分析是这一观点的印证，并补充了网络科学跨学科应用的图景。

最后，感谢集智网络科学社区陈关荣、史定华、陆君安等老师为本文贡献的专业观点和宝贵意见。也欢迎社区的技术力量加入计算社群，用技术和计算的力量促进内容创作、提升社区体验。

参考文献

[1] Watts, D., Strogatz, S. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998). https://doi.org/10.1038/30918

[2] Barabási, Albert-László, and Réka Albert. "Emergence of scaling in random networks."

Science 286.5439 (1999): 509-512.

[3] https://api.semanticscholar.org/graph/v1

[4] Wang, Dashun, Chaoming Song, and Albert-László Barabási. "Quantifying long-term scientific impact." Science 342.6154 (2013): 127-132.

[5] Radicchi, Filippo, Santo Fortunato, and Claudio Castellano. "Universality of citation distributions: Toward an objective measure of scientific impact." Proceedings of the National Academy of Sciences 105.45 (2008): 17268-17272.