English Blog | 中文博客
In the rapidly evolving field of real-time object detection, D-FINE emerges as a revolutionary approach that significantly surpasses existing models like YOLOv10, YOLO11, and RT-DETR v1/v2/v3, raising the performance ceiling for real-time object detection. After pretraining on the large-scale dataset Objects365, D-FINE far exceeds its competitor LW-DETR, achieving up to 59.3% AP on the COCO dataset while maintaining excellent frame rates, parameter counts, and computational complexity. This positions D-FINE as a leader in the realm of real-time object detection, laying the groundwork for future research advancements.
Currently, all code, weights, logs, compilation tools, and the FiftyOne visualization tool for D-FINE have been fully open-sourced, thanks to the codebase provided by RT-DETR. This includes pretraining tutorials, custom dataset tutorials, and more. We will continue to update with improvement insights and tuning strategies. We welcome everyone to raise issues and collectively promote the D-FINE series. We also hope you can leave a ⭐; it's the best encouragement for us.
GitHub Repo: https://github.com/Peterande/D-FINE
ArXiv Paper: https://arxiv.org/abs/2410.13842
D-FINE redefines the regression task in DETR-based object detectors as FDR, and based on this, develops a performance-enhancing self-distillation mechanism GO-LSD. Below is a brief introduction to FDR and GO-LSD:
- Initial Box Prediction: Similar to traditional DETR methods, the decoder of D-FINE transforms object queries into several initial bounding boxes in the first layer. These boxes do not need to be highly accurate and serve only as an initialization.
- Fine-Grained Distribution Optimization: Unlike traditional methods that directly decode new bounding boxes, D-FINE generates four sets of probability distributions based on these initial bounding boxes in the decoder layers and iteratively optimizes these distributions layer by layer. These distributions essentially act as a "fine-grained intermediate representation" of the detection boxes. Coupled with a carefully designed weighting function W(n), D-FINE can adjust the initial bounding boxes by fine-tuning these representations, allowing for subtle modifications or significant shifts of the edges (top, bottom, left, right). The specific process is illustrated in the figure:
For readability, we will not elaborate on the mathematical formulas and the Fine-Grained Localization (FGL) Loss that aids optimization here. Interested readers can refer to the original paper for derivations.
The main advantages of redefining the bounding box regression task as FDR are:
-
Simplified Supervision: While optimizing detection boxes using traditional L1 loss and IoU loss, the "residual" between labels and predictions can be additionally used to constrain these intermediate probability distributions. This allows each decoder layer to more effectively focus on and address the localization errors it currently faces. As the number of layers increases, their optimization objectives become progressively simpler, thereby simplifying the overall optimization process.
-
Robustness in Complex Scenarios: The values of these probability distributions inherently represent the confidence level of fine-tuning for each edge. This enables D-FINE to independently model the uncertainty of each edge at different network depths, thereby exhibiting stronger robustness in complex real-world scenarios such as occlusion, motion blur, and low-light conditions, compared to directly regressing four fixed values.
-
Flexible Optimization Mechanism: The probability distributions are transformed into final bounding box offsets through a weighted sum. The carefully designed weighting function ensures fine-grained adjustments when the initial box is accurate and provides significant corrections when necessary.
-
Research Potential and Scalability: By transforming the regression task into a probability distribution prediction problem consistent with classification tasks, FDR not only enhances compatibility with other tasks but also enables object detection models to benefit from innovations in areas such as knowledge distillation, multi-task learning, and distribution optimization, opening new avenues for future research.
GO-LSD (Global Optimal Localization Self-Distillation) Integrates Knowledge Distillation into FDR-Based Detectors Seamlessly
Based on the above, object detectors equipped with the FDR framework satisfy the following two points:
-
Ability to Achieve Knowledge Transfer: As Hinton mentioned in the paper "Distilling the Knowledge in a Neural Network", probabilities are "knowledge." The network's output becomes probability distributions, and these distributions carry localization knowledge. By calculating the KLD loss, this "knowledge" can be transferred from deeper layers to shallower layers. This is something that traditional fixed box representations (Dirac δ functions) cannot achieve.
-
Consistent Optimization Objectives: Since each decoder layer in the FDR framework shares a common goal: reducing the residual between the initial bounding box and the ground truth bounding box, the precise probability distributions generated by the final layer can serve as the ultimate target for each preceding layer and guide them through distillation.
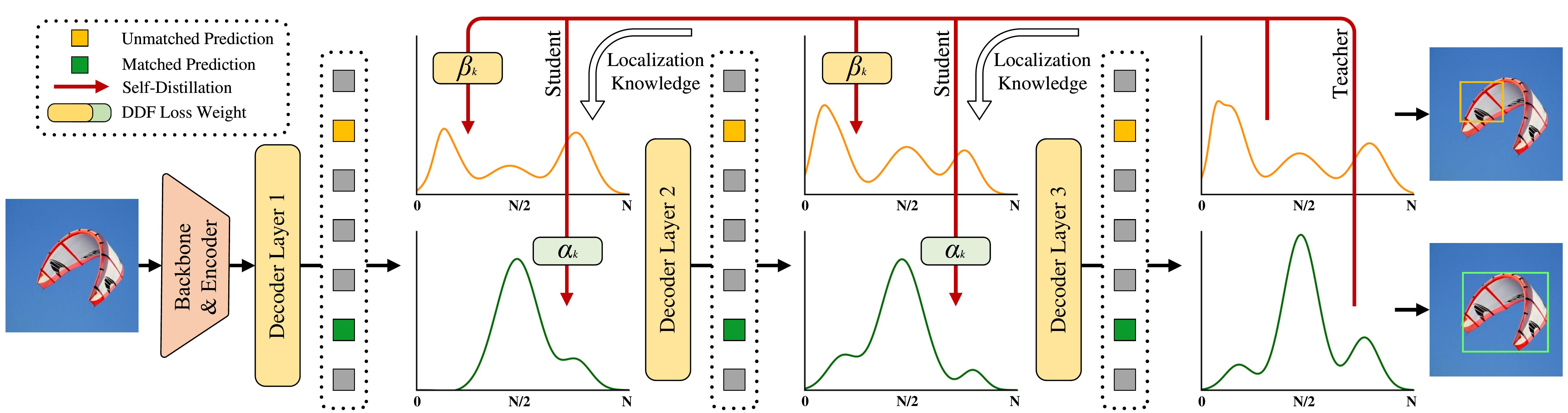
Thus, based on FDR, we propose GO-LSD (Global Optimal Localization Self-Distillation). By implementing localization knowledge distillation between network layers, we further extend the capabilities of D-FINE. The specific process is illustrated in the figure:
Similarly, for readability, we will not elaborate on the mathematical formulas and the Decoupled Distillation Focal (DDF) Loss that aids optimization here. Interested readers can refer to the original paper for derivations.
This results in a synergistic win-win effect: as training progresses, the predictions of the final layer become increasingly accurate, and its generated soft labels can better help the preceding layers improve prediction accuracy. Conversely, the earlier layers learn to localize accurately more quickly, simplifying the optimization tasks of the deeper layers and further enhancing overall accuracy.
The following visualization showcases D-FINE's predictions in various complex detection scenarios. These scenarios include occlusion, low-light conditions, motion blur, depth-of-field effects, and densely populated scenes. Despite these challenges, D-FINE still produces accurate localization results.
Additionally, the visualization below shows the prediction results of the first layer and the last layer, the corresponding distributions of the four edges, and the weighted distributions. It can be seen that the localization of the predicted boxes becomes more precise as the distributions are optimized.
Answer: No, FDR and the original prediction have almost no difference in speed, parameter count, and computational complexity, making it a seamless replacement.
Answer: The increase in training cost mainly comes from how to generate the labels of the distributions. We have optimized this process, keeping the increase in training time and memory consumption to 6% and 2%, respectively, making it almost negligible.
Answer: Directly applying FDR and GO-LSD will significantly improve performance but will not make the network faster or lighter. Therefore, we performed a series of lightweight optimizations on RT-DETR. These adjustments led to a performance drop, but our methods compensated for these losses, achieving a perfect balance of speed, parameters, computational complexity, and performance.