DLKoopman: A general-purpose Python package for Koopman theory using deep learning.
Koopman theory is a technique to encode sampled data (aka states) of a nonlinear dynamical system into a linear domain. This is very powerful as a linear model can:
- Give insight into the dynamics via eigenvalues and eigenvectors.
- Leverage linear algebra techniques to easily analyze the system and predict its behavior under unknown conditions.
DLKoopman uses deep learning to learn an encoding of a nonlinear dynamical system into a linear domain, while simultaneously learning the dynamics of the linear model. DLKoopman bridges the gap between:
- Software packages that restrict the learning of a good encoding (e.g.
pykoopman), and - Efforts that learn encodings for specific applications instead of being a general-purpose tool (e.g.
DeepKoopman).
- State prediction (
StatePred) - Train on individual states of a system, then predict unknown states.- E.g: What is the pressure vector on this aircraft for
$23.5^{\circ}$ angle of attack?
- E.g: What is the pressure vector on this aircraft for
- Trajectory prediction (
TrajPred) - Train on generated trajectories of a system, then predict unknown trajectories for new initial states.- E.g: What is the behavior of this pendulum if I start from the point
$[1,-1]$ ?
- E.g: What is the behavior of this pendulum if I start from the point
- General-purpose and reusable - supports data from any dynamical system.
- Novel error function Average Normalized Absolute Error (ANAE) for visualizing performance.
- Extensive options and a ready-to-use hyperparameter search module to improve performance.
- Built using Pytorch, supports both CPU and GPU platforms.
Read more about DLKoopman in this blog article.
pip install dlkoopman
git clone https://github.com/GaloisInc/dlkoopman.git
cd dlkoopman
pip install .
DLKoopman can also be run as a docker container by pulling the image from galoisinc/dlkoopman:<version>, e.g. docker pull galoisinc/dlkoopman:v1.1.3.
Available in the examples folder.
Available at https://galoisinc.github.io/dlkoopman/.
See Releases and their notes.
Assume a dynamical system
For a thorough mathematical treatment, see this technical report.
This is a small example with three input states
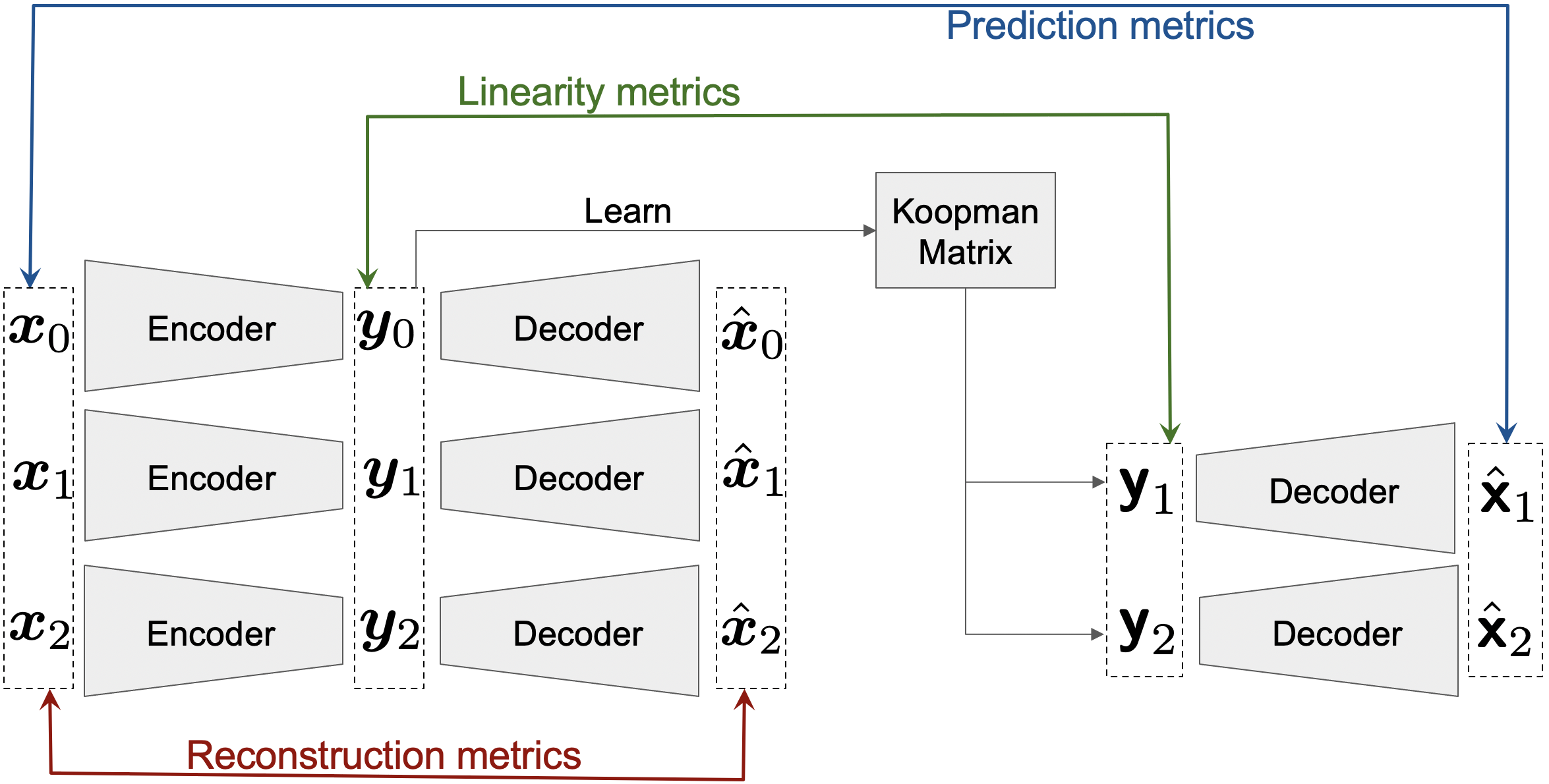
Errors mimimized during training:
- Train the autoencoder - Reconstruction
reconbetween$x$ and$\hat{x}$ . - Train the Koopman matrix - Linearity
linbetween$y$ and$\mathsf{y}$ . - Combine the above - Prediction
predbetween$x$ and$\hat{\mathsf{x}}$ .
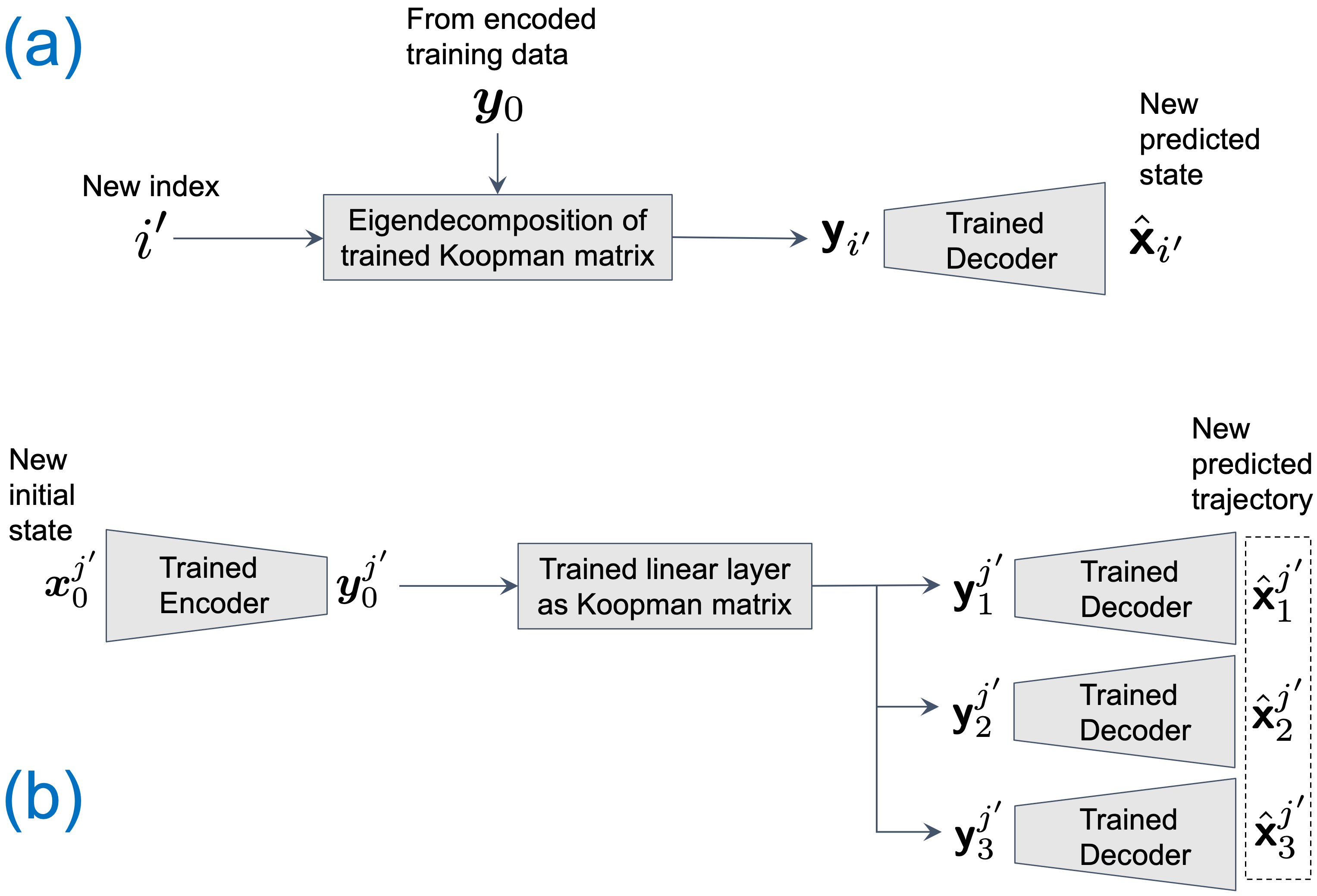
Prediction happens after training.
(a) State prediction - Compute predicted states for new indexes such as
(b) Trajectory prediction - Generate predicted trajectories
Some common issues and ways to overcome them are described in the known issues.
Please cite the accompanying paper:
@inproceedings{Dey2023_L4DC,
author = {Sourya Dey and Eric William Davis},
title = {{DLKoopman: A deep learning software package for Koopman theory}},
booktitle = {Proceedings of The 5th Annual Learning for Dynamics and Control Conference},
pages = {1467--1479},
volume = {211},
series = {Proceedings of Machine Learning Research},
publisher = {PMLR},
year = {2023},
month = {Jun}
}
- B. O. Koopman - Hamiltonian systems and transformation in Hilbert space
- J. Nathan Kutz, Steven L. Brunton, Bingni Brunton, Joshua L. Proctor - Dynamic Mode Decomposition
- Bethany Lusch, J. Nathan Kutz & Steven L. Brunton - Deep learning for universal linear embeddings of nonlinear dynamics
This material is based upon work supported by the United States Air Force and DARPA under Contract No. FA8750-20-C-0534. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the United States Air Force and DARPA. Distribution Statement A, "Approved for Public Release, Distribution Unlimited."