1. 位运算简介

1.1 位运算与二进制简介

位运算（Bit Operation）：在计算机内部，数是以「二进制（Binary）」的形式来进行存储。位运算就是直接对数的二进制进行计算操作，在程序中使用位运算进行操作，会大大提高程序的性能。

在学习二进制数的位运算之前，我们先来了解一下什么叫做「二进制数」。

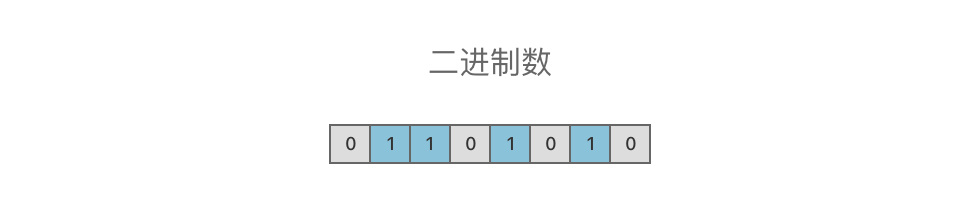
二进制数（Binary）：由 $0$ 和 $1$ 两个数码来表示的数。二进制数中每一个 $0$ 或每一个 $1$ 都称为一个「位（Bit）」。

我们通常使用的十进制数有 $0 \sim 9$ 共 $10$ 个数字，进位规则是「满十进一」。例如：

$7_{(10)} + 2_{(10)} = 9_{(10)}$：$7_{(10)}$ 加上 $2_{(10)}$ 等于 $9_{(10)}$。
$9_{(10)} + 2_{(10)} = 11_{(10)}$：$9_{(10)}$ 加上 $2_{(10)}$ 之后个位大于等于 $10$，符合「满十进一」，结果等于 $11_{(10)}$。

而在二进制数中，我们只有 $0$ 和 $1$ 两个数码，它的进位规则是「逢二进一」。例如：

$1_{(2)} + 0_{(2)} = 1_{(2)}$：$1_{(2)}$ 加上 $0_{(2)}$ 等于 $1_{(2)}$。
$1_{(2)} + 1_{(2)} = 10_{(2)}$：$1_{(2)}$ 加上 $1_{(2)}$，大于等于 $2$，符合「逢二进一」，结果等于 $10_{(2)}$。
$10_{(2)} + 1_{(2)} = 11_{(2)}$。

1.2 二进制数的转换

1.2.1 二进制转十进制数

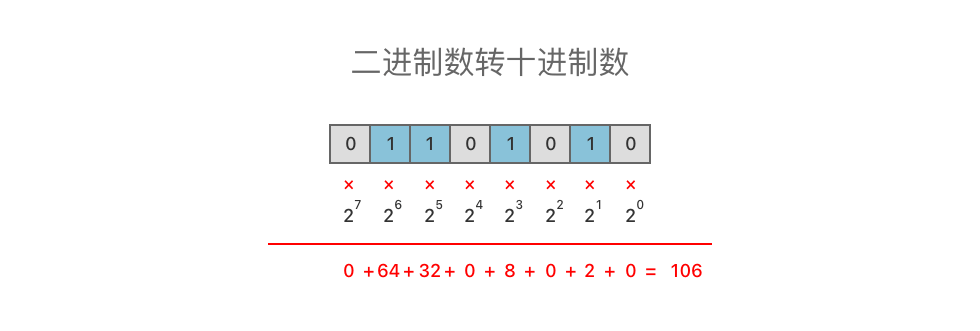
在十进制数中，数字 $2749_{(10)}$ 可以理解为 $2 \times 1000 + 7 \times 100 + 4 \times 10 + 9 * 1$，相当于 $2 \times 10^3 + 7 \times 10^2 + 4 \times 10^1 + 9 \times 10^0$，即 $2000 + 700 + 40 + 9 = 2749_{(10)}$。

同理，在二进制数中，$01101010_{(2)}$ 可以看作为 $(0 \times 2^7) + (1 \times 2^6) + (1 \times 2^5) + (0 \times 2^4) + (1 \times 2^3) + (0 \times 2^2) + (1 \times 2^1) + (0 \times 2^0)$，即 $0 + 64 + 32 + 0 + 8 + 0 + 2 + 0 = 106_{(10)}$。

我们可以通过这样的方式，将一个二进制数转为十进制数。

1.2.2 十进制转二进制数

十进制数转二进制数的方法是：除二取余，逆序排列法。

我们以十进制数中的 $106_{(10)}$ 为例。

$\begin{aligned} 106 \div 2 = 53 & \text{（余 0）} \cr 53 \div 2 = 26 & \text{（余 1）} \cr 26 \div 2 = 13 & \text{（余 0）} \cr 13 \div 2 = 6 & \text{（余 1）} \cr 6 \div 2 = 3 & \text{（余 0）} \cr 3 \div 2 = 1 & \text{（余 1）} \cr 1 \div 2 = 0 & \text{（余 1）} \cr 0 \div 2 = 0 & \text{（余 0）} \end{aligned}$

我们反向遍历每次计算的余数，依次是 $0$，$1$，$1$，$0$，$1$，$0$，$1$，$0$，即 $01101010_{(2)}$。

2. 位运算基础操作

在二进制的基础上，我们可以对二进制数进行相应的位运算。基本的位运算共有 $6$ 种，分别是：「按位与运算」、「按位或运算」、「按位异或运算」、「取反运算」、「左移运算」、「右移运算」。

这里的「按位与运算」、「按位或运算」、「按位异或运算」、「左移运算」、「右移运算」是双目运算。

「按位与运算」、「按位或运算」、「按位异或运算」是将两个整数作为二进制数，对二进制数表示中的每一位（即二进位）逐一进行相应运算，即双目运算。
「左移运算」、「右移运算」是将左侧整数作为二进制数，将右侧整数作为移动位数，然后对左侧二进制数的全部位进行移位运算，每次移动一位，总共移动右侧整数次位，也是双目运算。

而「取反运算」是单目运算，是对一个整数的二进制数进行的位运算。

我们先来看下这 $6$ 种位运算的规则，再来进行详细讲解。

运算符	描述	规则
`\|`	按位或运算符	只要对应的两个二进位有一个为 $1$ 时，结果位就为 $1$。
`&`	按位与运算符	只有对应的两个二进位都为 $1$ 时，结果位才为 $1$。
`<<`	左移运算符	将二进制数的各个二进位全部左移若干位。`<<` 右侧数字指定了移动位数，高位丢弃，低位补 $0$。
`>>`	右移运算符	对二进制数的各个二进位全部右移若干位。`>>` 右侧数字指定了移动位数，低位丢弃，高位补 $0$。
`^`	按位异或运算符	对应的两个二进位相异时，结果位为 $1$，二进位相同时则结果位为 $0$。
`~`	取反运算符	对二进制数的每个二进位取反，使数字 $1$ 变为 $0$，$0$ 变为 $1$。

2.1 按位与运算

按位与运算（AND）：按位与运算符为 &。其功能是对两个二进制数的每一个二进位进行与运算。

按位与运算规则：只有对应的两个二进位都为 $1$ 时，结果位才为 $1$。
- 1 & 1 = 1
- 1 & 0 = 0
- 0 & 1 = 0
- 0 & 0 = 0

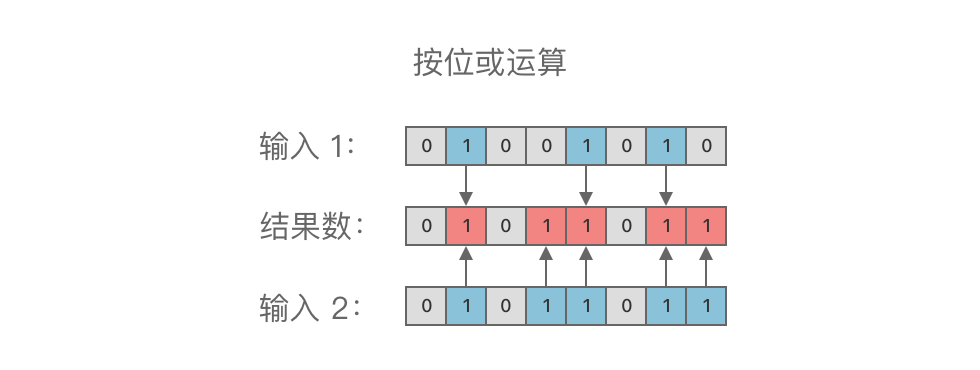
举个例子，对二进制数 $01111100_{(2)}$ 与 $00111110_{(2)}$ 进行按位与运算，结果为 $00111100_{(2)}$，如图所示：

2.2 按位或运算

按位或运算（OR）：按位或运算符为 |。其功能对两个二进制数的每一个二进位进行或运算。

按位或运算规则：只要对应的两个二进位有一个为 $1$ 时，结果位就为 $1$。
- 1 | 1 = 1
- 1 | 0 = 1
- 0 | 1 = 1
- 0 | 0 = 0

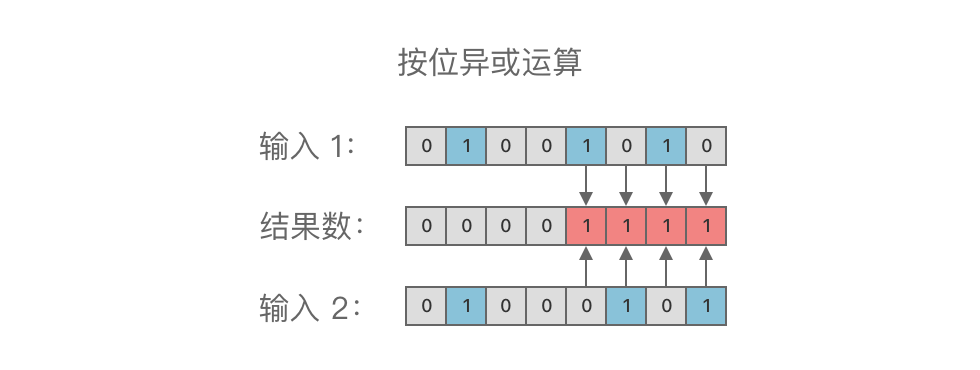
举个例子，对二进制数 $01001010_{(2)}$ 与 $01011011_{(2)}$ 进行按位或运算，结果为 $01011011_{(2)}$，如图所示：

2.3 按位异或运算

按位异或运算（XOR）：按位异或运算符为 ^。其功能是对两个二进制数的每一个二进位进行异或运算。

按位异或运算规则：对应的两个二进位相异时，结果位为 $1$，二进位相同时则结果位为 $0$。
0 ^ 0 = 0
1 ^ 0 = 1
0 ^ 1 = 1
1 ^ 1 = 0

举个例子，对二进制数 $01001010_{(2)}$ 与 $01000101_{(2)}$ 进行按位异或运算，结果为 $00001111_{(2)}$，如图所示：

2.4 取反运算

取反运算（NOT）：取反运算符为 ~。其功能是对一个二进制数的每一个二进位进行取反运算。

取反运算规则：使数字 $1$ 变为 $0$，$0$ 变为 $1$。
- ~0 = 1
- ~1 = 0

举个例子，对二进制数 $01101010_{(2)}$ 进行取反运算，结果如图所示：

2.5 左移运算和右移运算

左移运算（SHL）：左移运算符为 <<。其功能是对一个二进制数的各个二进位全部左移若干位（高位丢弃，低位补 $0$）。

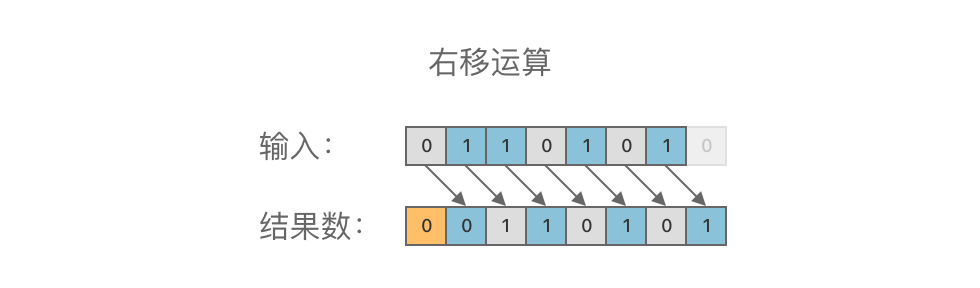
举个例子，对二进制数 $01101010_{(2)}$ 进行左移 $1$ 位运算，结果为 $11010100_{(2)}$，如图所示：

右移运算（SHR）：右移运算符为 >>。其功能是对一个二进制数的各个二进位全部右移若干位（低位丢弃，高位补 $0$）。

举个例子，对二进制数 $01101010_{(2)}$ 进行右移 $1$ 位运算，结果为 $00110101_{(2)}$，如图所示：

3. 位运算的应用

3.1 位运算的常用操作

3.1.1 判断整数奇偶

一个整数，只要是偶数，其对应二进制数的末尾一定为 $0$；只要是奇数，其对应二进制数的末尾一定为 $1$。所以，我们通过与 $1$ 进行按位与运算，即可判断某个数是奇数还是偶数。

(x & 1) == 0 为偶数。
(x & 1) == 1 为奇数。

3.1.2 二进制数选取指定位

如果我们想要从一个二进制数 $X$ 中取出某几位，使取出位置上的二进位保留原值，其余位置为 $0$，则可以使用另一个二进制数 $Y$，使该二进制数上对应取出位置为 $1$，其余位置为 $0$。然后令两个数进行按位与运算（X & Y），即可得到想要的数。

举个例子，比如我们要取二进制数 $X = 01101010_{(2)}$ 的末尾 $4$ 位，则只需将 $X = 01101010_{(2)}$ 与 $Y = 00001111_{(2)}$ (末尾 $4$ 位为 $1$，其余位为 $0$) 进行按位与运算，即 01101010 & 00001111 == 00001010。其结果 $00001010$ 就是我们想要的数（即二进制数 $01101010_{(2)}$ 的末尾 $4$ 位）。

3.1.3 将指定位设置为 $1$

如果我们想要把一个二进制数 $X$ 中的某几位设置为 $1$，其余位置保留原值，则可以使用另一个二进制数 $Y$，使得该二进制上对应选取位置为 $1$，其余位置为 $0$。然后令两个数进行按位或运算（X | Y），即可得到想要的数。

举个例子，比如我们想要将二进制数 $X = 01101010_{(2)}$ 的末尾 $4$ 位设置为 $1$，其余位置保留原值，则只需将 $X = 01101010_{(2)}$ 与 $Y = 00001111_{(2)}$（末尾 $4$ 位为 $1$，其余位为 $0$）进行按位或运算，即 01101010 | 00001111 = 01101111。其结果 $01101111$ 就是我们想要的数（即将二进制数 $01101010_{(2)}$ 的末尾 $4$ 位设置为 $1$，其余位置保留原值）。

3.1.4 反转指定位

如果我们想要把一个二进制数 $X$ 的某几位进行反转，则可以使用另一个二进制数 $Y$，使得该二进制上对应选取位置为 $1$，其余位置为 $0$。然后令两个数进行按位异或运算（X ^ Y），即可得到想要的数。

举个例子，比如想要将二进制数 $X = 01101010_{(2)}$ 的末尾 $4$ 位进行反转，则只需将 $X = 01101010_{(2)}$ 与 $Y = 00001111_{(2)}$（末尾 $4$ 位为 $1$，其余位为 $0$）进行按位异或运算，即 01101010 ^ 00001111 = 01100101。其结果 $01100101$ 就是我们想要的数（即将二进制数 $X = 01101010_{(2)}$ 的末尾 $4$ 位进行反转）。

3.1.5 交换两个数

通过按位异或运算可以实现交换两个数的目的（只能用于交换两个整数）。

a, b = 10, 20
a ^= b
b ^= a
a ^= b
print(a, b)

3.1.6 将二进制最右侧为 $1$ 的二进位改为 $0$

如果我们想要将一个二进制数 $X$ 最右侧为 $1$ 的二进制位改为 $0$，则只需通过 X & (X - 1) 的操作即可完成。

比如 $X = 01101100_{(2)}$，$X - 1 = 01101011_{(2)}$，则 X & (X - 1) == 01101100 & 01101011 == 01101000，结果为 $01101000_{(2)}$（即将 $X$ 最右侧为 $1$ 的二进制为改为 $0$）。

3.1.7 计算二进制中二进位为 $1$ 的个数

从 3.1.6 中得知，通过 X & (X - 1) 我们可以将二进制 $X$ 最右侧为 $1$ 的二进制位改为 $0$，那么如果我们不断通过 X & (X - 1) 操作，最终将二进制 $X$ 变为 $0$，并统计执行次数，则可以得到二进制中二进位为 $1$ 的个数。

具体代码如下：

class Solution:
    def hammingWeight(self, n: int) -> int:
        cnt = 0
        while n:
            n = n & (n - 1)
            cnt += 1
        return cnt

3.1.8 判断某数是否为 $2$ 的幂次方

通过判断 X & (X - 1) == 0 是否成立，即可判断 $X$ 是否为 $2$ 的幂次方。

这是因为：

凡是 $2$ 的幂次方，其二进制数的某一高位为 $1$，并且仅此高位为 $1$，其余位都为 $0$。比如：$4_{(10)} = 00000100_{(2)}$、$8_{(10)} = 00001000_{(2)}$。
不是 $2$ 的幂次方，其二进制数存在多个值为 $1$ 的位。比如：$5_{10} = 00000101_{(2)}$、$6_{10} = 00000110_{(2)}$。

接下来我们使用 X & (X - 1) 操作，将原数对应二进制数最右侧为 $1$ 的二进位改为 $0$ 之后，得到新值：

如果原数是 $2$ 的幂次方，则通过 X & (X - 1) 操作之后，新值所有位都为 $0$，值为 $0$。
如果该数不是 $2$ 的幂次方，则通过 X & (X - 1) 操作之后，新值仍存在不为 $0$ 的位，值肯定不为 $0$。

所以我们可以通过是否为 $0$ 即可判断该数是否为 $2$ 的幂次方。

3.2 位运算的常用操作总结

功能	位运算	示例
从右边开始，把最后一个 $1$ 改写成 $0$	`x & (x - 1)`	`100101000 -> 100100000`
去掉右边起第一个 $1$ 的左边	`x & (x ^ (x - 1))` 或 `x & (-x)`	`100101000 -> 1000`
去掉最后一位	`x >> 1`	`101101 -> 10110`
取右数第 $k$ 位	`x >> (k - 1) & 1`	`1101101 -> 1, k = 4`
取末尾 $3$ 位	`x & 7`	`1101101 -> 101`
取末尾 $k$ 位	`x & 15`	`1101101 -> 1101, k = 4`
只保留右边连续的 $1$	`(x ^ (x + 1)) >> 1`	`100101111 -> 1111`
右数第 $k$ 位取反	`x ^ (1 << (k - 1))`	`101001 -> 101101, k = 3`
在最后加一个 $0$	`x << 1`	`101101 -> 1011010`
在最后加一个 $1$	`(x << 1) + 1`	`101101 -> 1011011`
把右数第 $k$ 位变成 $0$	`x & ~(1 << (k - 1))`	`101101 -> 101001, k = 3`
把右数第 $k$ 位变成 $1$	`x \| (1 << (k - 1))`	`101001 -> 101101, k = 3`
把右边起第一个 $0$ 变成 $1$	`x \| (x + 1)`	`100101111 -> 100111111`
把右边连续的 $0$ 变成 $1$	`x \| (x - 1)`	`11011000 -> 11011111`
把右边连续的 $1$ 变成 $0$	`x & (x + 1)`	`100101111 -> 100100000`
把最后一位变成 $0$	`x \| 1 - 1`	`101101 -> 101100`
把最后一位变成 $1$	`x \| 1`	`101100 -> 101101`
把末尾 $k$ 位变成 $1$	`x \| (1 << k - 1)`	`101001 -> 101111, k = 4`
最后一位取反	`x ^ 1`	`101101 -> 101100`
末尾 $k$ 位取反	`x ^ (1 << k - 1)`	`101001 -> 100110, k = 4`

3.3 二进制枚举子集

除了上面的这些常见操作，我们经常常使用二进制数第 $1 \sim n$ 位上 $0$ 或 $1$ 的状态来表示一个由 $1 \sim n$ 组成的集合。也就是说通过二进制来枚举子集。

3.3.1 二进制枚举子集简介

先来介绍一下「子集」的概念。

子集：如果集合 $A$ 的任意一个元素都是集合 $S$ 的元素，则称集合 $A$ 是集合 $S$ 的子集。可以记为 $A \in S$。

有时候我们会遇到这样的问题：给定一个集合 $S$，枚举其所有可能的子集。

枚举子集的方法有很多，这里介绍一种简单有效的枚举方法：「二进制枚举子集算法」。

对于一个元素个数为 $n$ 的集合 $S$ 来说，每一个位置上的元素都有选取和未选取两种状态。我们可以用数字 $1$ 来表示选取该元素，用数字 $0$ 来表示不选取该元素。

那么我们就可以用一个长度为 $n$ 的二进制数来表示集合 $S$ 或者表示 $S$ 的子集。其中二进制的每一个二进位都对应了集合中某一个元素的选取状态。对于集合中第 $i$ 个元素来说，二进制对应位置上的 $1$ 代表该元素被选取，$0$ 代表该元素未被选取。

举个例子，比如长度为 $5$ 的集合 $S = \lbrace 5, 4, 3, 2, 1 \rbrace$，我们可以用一个长度为 $5$ 的二进制数来表示该集合。

比如二进制数 $11111_{(2)}$ 就表示选取集合的第 $1$ 位、第 $2$ 位、第 $3$ 位、第 $4$ 位、第 $5$ 位元素，也就是集合 $\lbrace 5, 4, 3, 2, 1 \rbrace$，即集合 $S$ 本身。如下表所示：

集合 S 中元素位置	5	4	3	2	1
二进位对应值	1	1	1	1	1
对应选取状态	选取	选取	选取	选取	选取

再比如二进制数 $10101_{(2)}$ 就表示选取集合的第 $1$ 位、第 $3$ 位、第 $5$ 位元素，也就是集合 $\lbrace 5, 3, 1 \rbrace$。如下表所示：

集合 S 中元素位置	5	4	3	2	1
二进位对应值	1	0	1	0	1
对应选取状态	选取	未选取	选取	未选取	选取

再比如二进制数 $01001_{(2)}$ 就表示选取集合的第 $1$ 位、第 $4$ 位元素，也就是集合 $\lbrace 4, 1 \rbrace$。如下标所示：

集合 S 中元素位置	5	4	3	2	1
二进位对应值	0	1	0	0	1
对应选取状态	未选取	选取	未选取	未选取	选取

通过上面的例子我们可以得到启发：对于长度为 $5$ 的集合 $S$ 来说，我们只需要从 $00000 \sim 11111$ 枚举一次（对应十进制为 $0 \sim 2^5 - 1$）即可得到长度为 $5$ 的集合 $S$ 的所有子集。

我们将上面的例子拓展到长度为 $n$ 的集合 $S$。可以总结为：

对于长度为 $n$ 的集合 $S$ 来说，只需要枚举 $0 \sim 2^n - 1$（共 $2^n$ 种情况），即可得到集合 $S$ 的所有子集。

3.3.2 二进制枚举子集代码

class Solution:
    def subsets(self, S):                   # 返回集合 S 的所有子集
        n = len(S)                          # n 为集合 S 的元素个数
        sub_sets = []                       # sub_sets 用于保存所有子集
        for i in range(1 << n):             # 枚举 0 ~ 2^n - 1
            sub_set = []                    # sub_set 用于保存当前子集
            for j in range(n):              # 枚举第 i 位元素
                if i >> j & 1:              # 如果第 i 为元素对应二进位删改为 1，则表示选取该元素
                    sub_set.append(S[j])    # 将选取的元素加入到子集 sub_set 中
            sub_sets.append(sub_set)        # 将子集 sub_set 加入到所有子集数组 sub_sets 中
        return sub_sets                     # 返回所有子集

参考资料

【博文】Python 中的按位运算符 |【生长吧！Python!】- 云社区 - 华为云
【博文】一文读懂位运算的使用 - 小黑说 Java - 掘金
【博文】枚举排列和枚举子集 - CUC ACM-Wiki
【博文】Swift 运算符 | 菜鸟教程

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

01.Bit-Operation.md

01.Bit-Operation.md

1. 位运算简介

1.1 位运算与二进制简介

1.2 二进制数的转换

1.2.1 二进制转十进制数

1.2.2 十进制转二进制数

2. 位运算基础操作

2.1 按位与运算

2.2 按位或运算

2.3 按位异或运算

2.4 取反运算

2.5 左移运算和右移运算

3. 位运算的应用

3.1 位运算的常用操作

3.1.1 判断整数奇偶

3.1.2 二进制数选取指定位

3.1.3 将指定位设置为 $1$

3.1.4 反转指定位

3.1.5 交换两个数

3.1.6 将二进制最右侧为 $1$ 的二进位改为 $0$

3.1.7 计算二进制中二进位为 $1$ 的个数

3.1.8 判断某数是否为 $2$ 的幂次方

3.2 位运算的常用操作总结

3.3 二进制枚举子集

3.3.1 二进制枚举子集简介

3.3.2 二进制枚举子集代码

参考资料

Files

01.Bit-Operation.md

Latest commit

History

01.Bit-Operation.md

File metadata and controls

1. 位运算简介

1.1 位运算与二进制简介

1.2 二进制数的转换

1.2.1 二进制转十进制数

1.2.2 十进制转二进制数

2. 位运算基础操作

2.1 按位与运算

2.2 按位或运算

2.3 按位异或运算

2.4 取反运算

2.5 左移运算和右移运算

3. 位运算的应用

3.1 位运算的常用操作

3.1.1 判断整数奇偶

3.1.2 二进制数选取指定位

3.1.3 将指定位设置为 $1$

3.1.4 反转指定位

3.1.5 交换两个数

3.1.6 将二进制最右侧为 $1$ 的二进位改为 $0$

3.1.7 计算二进制中二进位为 $1$ 的个数

3.1.8 判断某数是否为 $2$ 的幂次方

3.2 位运算的常用操作总结

3.3 二进制枚举子集

3.3.1 二进制枚举子集简介

3.3.2 二进制枚举子集代码

参考资料