01.Array-Sliding-Window.md

1. 滑动窗口算法介绍

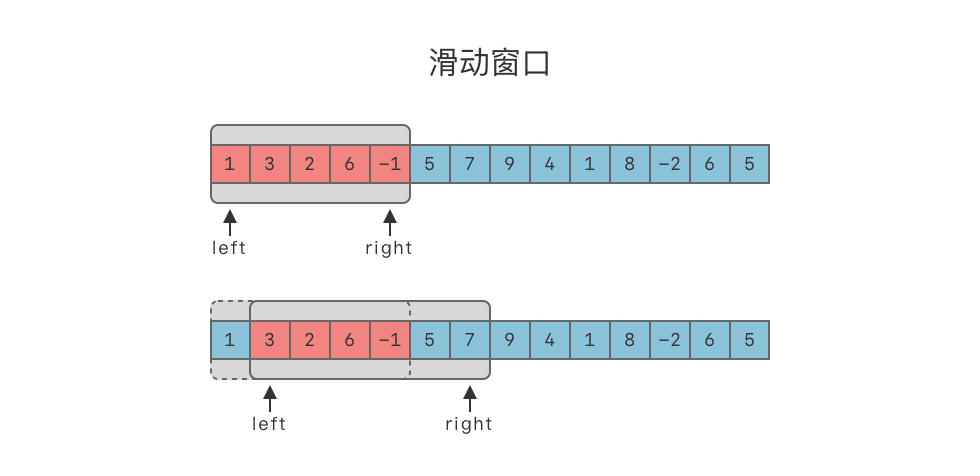
在计算机网络中，滑动窗口协议（Sliding Window Protocol）是传输层进行流控的一种措施，接收方通过通告发送方自己的窗口大小，从而控制发送方的发送速度，从而达到防止发送方发送速度过快而导致自己被淹没的目的。我们所要讲解的滑动窗口算法也是利用了同样的特性。

滑动窗口算法（Sliding Window）：在给定数组 / 字符串上维护一个固定长度或不定长度的窗口。可以对窗口进行滑动操作、缩放操作，以及维护最优解操作。

• 滑动操作：窗口可按照一定方向进行移动。最常见的是向右侧移动。
• 缩放操作：对于不定长度的窗口，可以从左侧缩小窗口长度，也可以从右侧增大窗口长度。

滑动窗口利用了双指针中的快慢指针技巧，我们可以将滑动窗口看做是快慢指针两个指针中间的区间，也可以将滑动窗口看做是快慢指针的一种特殊形式。

2. 滑动窗口适用范围

滑动窗口算法一般用来解决一些查找满足一定条件的连续区间的性质（长度等）的问题。该算法可以将一部分问题中的嵌套循环转变为一个单循环，因此它可以减少时间复杂度。

按照窗口长度的固定情况，我们可以将滑动窗口题目分为以下两种：

• 固定长度窗口：窗口大小是固定的。
• 不定长度窗口：窗口大小是不固定的。
  • 求解最大的满足条件的窗口。
  • 求解最小的满足条件的窗口。

下面来分别讲解一下这两种类型题目。

3. 固定长度滑动窗口

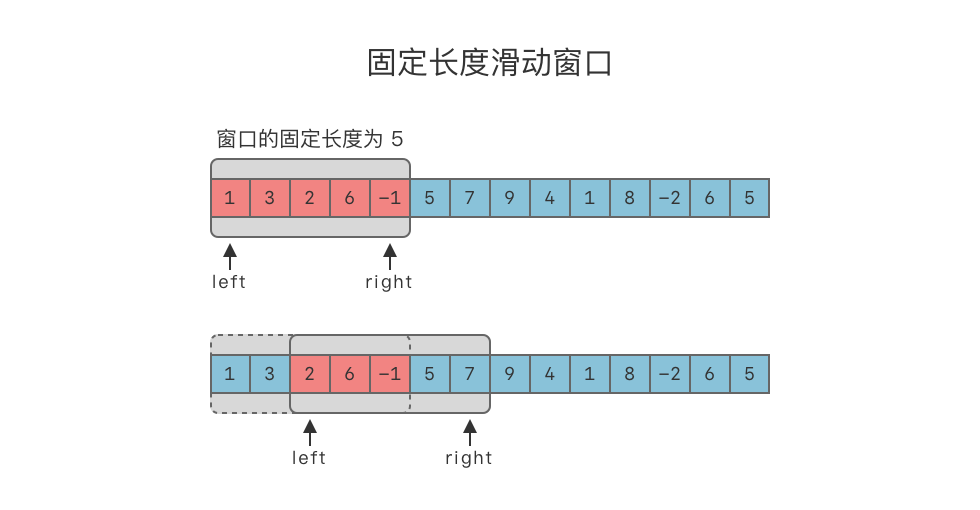
固定长度滑动窗口算法（Fixed Length Sliding Window）：在给定数组 / 字符串上维护一个固定长度的窗口。可以对窗口进行滑动操作、缩放操作，以及维护最优解操作。

3.1 固定长度滑动窗口算法步骤

假设窗口的固定大小为 $window\underline{}size$。

1. 使用两个指针 $left$、$right$。初始时，$left$、$right$ 都指向序列的第一个元素，即：$left = 0$，$right = 0$，区间 $[left, right]$ 被称为一个「窗口」。
2. 当窗口未达到 $window\underline{}size$ 大小时，不断移动 $right$，先将数组前 $window\underline{}size$ 个元素填入窗口中，即 window.append(nums[right])。
3. 当窗口达到 $window\underline{}size$ 大小时，即满足 right - left + 1 >= window_size 时，判断窗口内的连续元素是否满足题目限定的条件。
   1. 如果满足，再根据要求更新最优解。
   2. 然后向右移动 $left$，从而缩小窗口长度，即 left += 1，使得窗口大小始终保持为 $window\underline{}size$。
4. 向右移动 $right$，将元素填入窗口中，即 window.append(nums[right])。
5. 重复 $2 \sim 4$ 步，直到 $right$ 到达数组末尾。

3.2 固定长度滑动窗口代码模板

left = 0
right = 0

while right < len(nums):
    window.append(nums[right])
    
    # 超过窗口大小时，缩小窗口，维护窗口中始终为 window_size 的长度
    if right - left + 1 >= window_size:
        # ... 维护答案
        window.popleft()
        left += 1
    
    # 向右侧增大窗口
    right += 1

下面我们根据具体例子来讲解一下如何使用固定窗口大小的滑动窗口来解决问题。

3.3 大小为 K 且平均值大于等于阈值的子数组数目

3.3.1 题目链接

• 1343. 大小为 K 且平均值大于等于阈值的子数组数目 - 力扣（LeetCode）

3.3.2 题目大意

描述：给定一个整数数组 $arr$ 和两个整数 $k$ 和 $threshold$ 。

要求：返回长度为 $k$ 且平均值大于等于 $threshold$ 的子数组数目。

说明：

• $1 \le arr.length \le 10^5$。
• $1 \le arr[i] \le 10^4$。
• $1 \le k \le arr.length$。
• $0 \le threshold \le 10^4$。

示例：

• 示例 1：

输入：arr = [2,2,2,2,5,5,5,8], k = 3, threshold = 4
输出：3
解释：子数组 [2,5,5],[5,5,5] 和 [5,5,8] 的平均值分别为 4，5 和 6 。其他长度为 3 的子数组的平均值都小于 4 （threshold 的值)。

• 示例 2：

输入：arr = [11,13,17,23,29,31,7,5,2,3], k = 3, threshold = 5
输出：6
解释：前 6 个长度为 3 的子数组平均值都大于 5 。注意平均值不是整数。

3.3.3 解题思路

思路 1：滑动窗口（固定长度）

这道题目是典型的固定窗口大小的滑动窗口题目。窗口大小为 $k$。具体做法如下：

1. $ans$ 用来维护答案数目。$window\underline{}sum$ 用来维护窗口中元素的和。
2. $left$ 、$right$ 都指向序列的第一个元素，即：$left = 0$，$right = 0$。
3. 向右移动 $right$，先将 $k$ 个元素填入窗口中，即 window_sum += arr[right]。
4. 当窗口元素个数为 $k$ 时，即满足 right - left + 1 >= k 时，判断窗口内的元素和平均值是否大于等于阈值 $threshold$。
   1. 如果满足，则答案数目加 $1$。
   2. 然后向右移动 $left$，从而缩小窗口长度，即 left += 1，使得窗口大小始终保持为 $k$。
5. 重复 $3 \sim 4$ 步，直到 $right$ 到达数组末尾。
6. 最后输出答案数目。

思路 1：代码

class Solution:
    def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:
        left = 0
        right = 0
        window_sum = 0
        ans = 0

        while right < len(arr):
            window_sum += arr[right]
            
            if right - left + 1 >= k:
                if window_sum >= k * threshold:
                    ans += 1
                window_sum -= arr[left]
                left += 1

            right += 1

        return ans

思路 1：复杂度分析

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(n)$。

4. 不定长度滑动窗口

不定长度滑动窗口算法（Sliding Window）：在给定数组 / 字符串上维护一个不定长度的窗口。可以对窗口进行滑动操作、缩放操作，以及维护最优解操作。

4.1 不定长度滑动窗口算法步骤

1. 使用两个指针 $left$、$right$。初始时，$left$、$right$ 都指向序列的第一个元素。即：$left = 0$，$right = 0$，区间 $[left, right]$ 被称为一个「窗口」。
2. 将区间最右侧元素添加入窗口中，即 window.add(s[right])。
3. 然后向右移动 $right$，从而增大窗口长度，即 right += 1。直到窗口中的连续元素满足要求。
4. 此时，停止增加窗口大小。转向不断将左侧元素移出窗口，即 window.popleft(s[left])。
5. 然后向右移动 $left$，从而缩小窗口长度，即 left += 1。直到窗口中的连续元素不再满足要求。
6. 重复 2 ~ 5 步，直到 $right$ 到达序列末尾。

4.2 不定长度滑动窗口代码模板

left = 0
right = 0

while right < len(nums):
    window.append(nums[right])
    
    while 窗口需要缩小:
        # ... 可维护答案
        window.popleft()
        left += 1
    
    # 向右侧增大窗口
    right += 1

4.3 无重复字符的最长子串

4.3.1 题目链接

• 3. 无重复字符的最长子串 - 力扣（LeetCode）

4.3.2 题目大意

描述：给定一个字符串 $s$。

要求：找出其中不含有重复字符的最长子串的长度。

说明：

• $0 \le s.length \le 5 * 10^4$。
• $s$ 由英文字母、数字、符号和空格组成。

示例：

• 示例 1：

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

• 示例 2：

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

4.3.3 解题思路

思路 1：滑动窗口（不定长度）

用滑动窗口 $window$ 来记录不重复的字符个数，$window$ 为哈希表类型。

1. 设定两个指针：$left$、$right$，分别指向滑动窗口的左右边界，保证窗口中没有重复字符。
2. 一开始，$left$、$right$ 都指向 $0$。
3. 向右移动 $right$，将最右侧字符 $s[right]$ 加入当前窗口 $window$ 中，记录该字符个数。
4. 如果该窗口中该字符的个数多于 $1$ 个，即 $window[s[right]] > 1$，则不断右移 $left$，缩小滑动窗口长度，并更新窗口中对应字符的个数，直到 $window[s[right]] \le 1$。
5. 维护更新无重复字符的最长子串长度。然后继续右移 $right$，直到 $right \ge len(nums)$ 结束。
6. 输出无重复字符的最长子串长度。

思路 1：代码

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        left = 0
        right = 0
        window = dict()
        ans = 0

        while right < len(s):
            if s[right] not in window:
                window[s[right]] = 1
            else:
                window[s[right]] += 1

            while window[s[right]] > 1:
                window[s[left]] -= 1
                left += 1

            ans = max(ans, right - left + 1)
            right += 1

        return ans

思路 1：复杂度分析

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(| \sum |)$。其中 $\sum$ 表示字符集，$| \sum |$ 表示字符集的大小。

4.4 长度最小的子数组

4.4.1 题目链接

• 209. 长度最小的子数组 - 力扣（LeetCode）

4.4.2 题目大意

描述：给定一个只包含正整数的数组 $nums$ 和一个正整数 $target$。

要求：找出数组中满足和大于等于 $target$ 的长度最小的「连续子数组」，并返回其长度。如果不存在符合条件的子数组，返回 $0$。

说明：

• $1 \le target \le 10^9$。
• $1 \le nums.length \le 10^5$。
• $1 \le nums[i] \le 10^5$。

示例：

• 示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

• 示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

4.4.3 解题思路

思路 1：滑动窗口（不定长度）

最直接的做法是暴力枚举，时间复杂度为 $O(n^2)$。但是我们可以利用滑动窗口的方法，在时间复杂度为 $O(n)$ 的范围内解决问题。

用滑动窗口来记录连续子数组的和，设定两个指针：$left$、$right$，分别指向滑动窗口的左右边界，保证窗口中的和刚好大于等于 $target$。

1. 一开始，$left$、$right$ 都指向 $0$。
2. 向右移动 $right$，将最右侧元素加入当前窗口和 $window\underline{}sum$ 中。
3. 如果 $window\underline{}sum \ge target$，则不断右移 $left$，缩小滑动窗口长度，并更新窗口和的最小值，直到 $window\underline{}sum < target$。
4. 然后继续右移 $right$，直到 $right \ge len(nums)$ 结束。
5. 输出窗口和的最小值作为答案。

思路 1：代码

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        size = len(nums)
        ans = size + 1
        left = 0
        right = 0
        window_sum = 0

        while right < size:
            window_sum += nums[right]

            while window_sum >= target:
                ans = min(ans, right - left + 1)
                window_sum -= nums[left]
                left += 1

            right += 1

        return ans if ans != size + 1 else 0

思路 1：复杂度分析

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(1)$。

4.5 乘积小于K的子数组

4.5.1 题目链接

• 713. 乘积小于K的子数组 - 力扣（LeetCode）

4.5.2 题目大意

描述：给定一个正整数数组 $nums$ 和整数 $k$。

要求：找出该数组内乘积小于 $k$ 的连续的子数组的个数。

说明：

• $1 \le nums.length \le 3 * 10^4$。
• $1 \le nums[i] \le 1000$。
• $0 \le k \le 10^6$。

示例：

• 示例 1：

输入：nums = [10,5,2,6], k = 100
输出：8
解释：8 个乘积小于 100 的子数组分别为：[10]、[5]、[2],、[6]、[10,5]、[5,2]、[2,6]、[5,2,6]。需要注意的是 [10,5,2] 并不是乘积小于 100 的子数组。

• 示例 2：

输入：nums = [1,2,3], k = 0
输出：0

4.5.3 解题思路

思路 1：滑动窗口（不定长度）

1. 设定两个指针：$left$、$right$，分别指向滑动窗口的左右边界，保证窗口内所有数的乘积 $window\underline{}product$ 都小于 $k$。使用 $window\underline{}product$ 记录窗口中的乘积值，使用 $count$ 记录符合要求的子数组个数。
2. 一开始，$left$、$right$ 都指向 $0$。
3. 向右移动 $right$，将最右侧元素加入当前子数组乘积 $window\underline{}product$ 中。
4. 如果 $window\underline{}product \ge k$，则不断右移 $left$，缩小滑动窗口长度，并更新当前乘积值 $window\underline{}product$ 直到 $window\underline{}product < k$。
5. 记录累积答案个数加 $1$，继续右移 $right$，直到 $right \ge len(nums)$ 结束。
6. 输出累积答案个数。

思路 1：代码

class Solution:
    def numSubarrayProductLessThanK(self, nums: List[int], k: int) -> int:
        if k <= 1:
            return 0

        size = len(nums)
        left = 0
        right = 0
        window_product = 1
        
        count = 0
        
        while right < size:
            window_product *= nums[right]

            while window_product >= k:
                window_product /= nums[left]
                left += 1

            count += (right - left + 1)
            right += 1
            
        return count

思路 1：复杂度分析

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(1)$。

参考资料

• 【答案】TCP 协议的滑动窗口具体是怎样控制流量的？ - 知乎
• 【博文】滑动窗口算法基本原理与实践 - huansky - 博客园
• 【博文】滑动窗口（Sliding Window）- lucifer.ren