03.Array-Insertion-Sort.md

1. 插入排序算法思想

插入排序（Insertion Sort）基本思想：

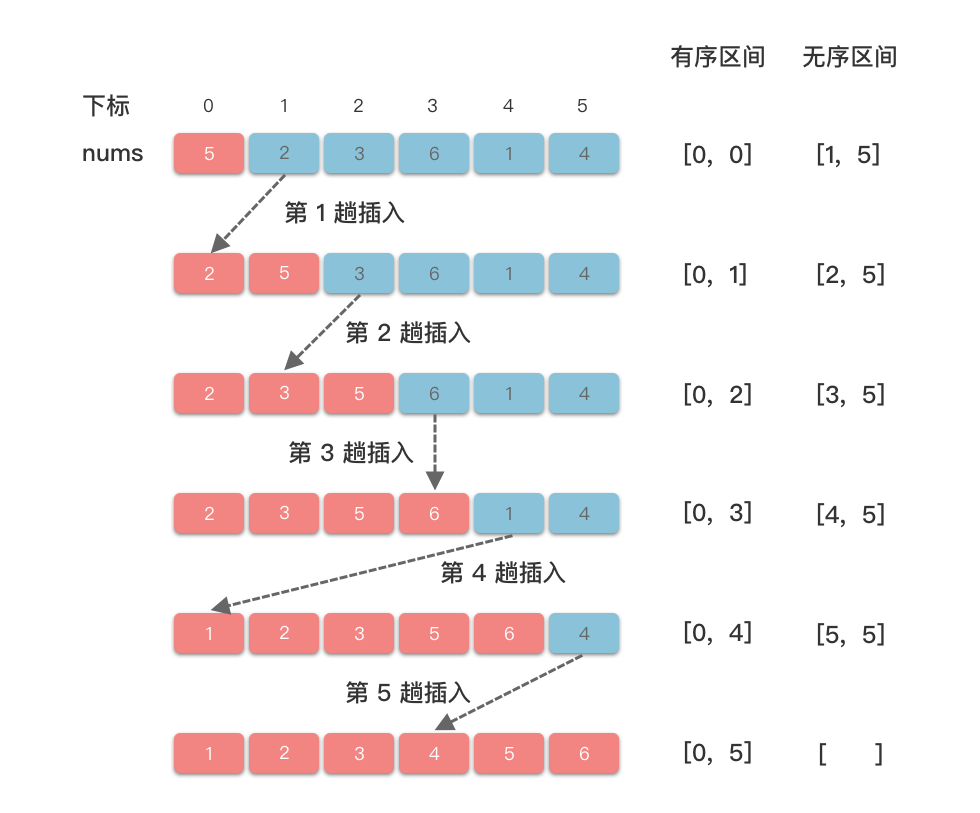
将数组分为两个区间：左侧为有序区间，右侧为无序区间。每趟从无序区间取出一个元素，然后将其插入到有序区间的适当位置。

插入排序在每次插入一个元素时，该元素会在有序区间找到合适的位置，因此每次插入后，有序区间都会保持有序。

2. 插入排序算法步骤

假设数组的元素个数为 $n$ 个，则插入排序的算法步骤如下：

1. 初始状态下，有序区间为 $[0, 0]$，无序区间为 $[1, n - 1]$。
2. 第 $1$ 趟插入：
   1. 取出无序区间 $[1, n - 1]$ 中的第 $1$ 个元素，即 $nums[1]$。
   2. 从右到左遍历有序区间中的元素，将比 $nums[1]$ 小的元素向后移动 $1$ 位。
   3. 如果遇到大于或等于 $nums[1]$ 的元素时，说明找到了插入位置，将 $nums[1]$ 插入到该位置。
   4. 插入元素后有序区间变为 $[0, 1]$，无序区间变为 $[2, n - 1]$。
3. 第 $2$ 趟插入：
   1. 取出无序区间 $[2, n - 1]$ 中的第 $1$ 个元素，即 $nums[2]$。
   2. 从右到左遍历有序区间中的元素，将比 $nums[2]$ 小的元素向后移动 $1$ 位。
   3. 如果遇到大于或等于 $nums[2]$ 的元素时，说明找到了插入位置，将 $nums[2]$ 插入到该位置。
   4. 插入元素后有序区间变为 $[0, 2]$，无序区间变为 $[3, n - 1]$。
4. 依次类推，对剩余无序区间中的元素重复上述插入过程，直到所有元素都插入到有序区间中，排序结束。

我们以 $[5, 2, 3, 6, 1, 4]$ 为例，演示一下插入排序的整个过程。

3. 插入排序代码实现

class Solution:
    def insertionSort(self, nums: [int]) -> [int]:
        # 遍历无序区间
        for i in range(1, len(nums)):
            temp = nums[i]
            j = i
            # 从右至左遍历有序区间
            while j > 0 and nums[j - 1] > temp:
                # 将有序区间中插入位置右侧的元素依次右移一位
                nums[j] = nums[j - 1]
                j -= 1
            # 将该元素插入到适当位置
            nums[j] = temp

        return nums

    def sortArray(self, nums: [int]) -> [int]:
        return self.insertionSort(nums)

4. 插入排序算法分析

• 最佳时间复杂度：$O(n)$。最好的情况下（初始时区间已经是升序排列），每个元素只进行一次元素之间的比较，因而总的比较次数最少，为 $∑^n_{i = 2}1 = n − 1$，并不需要移动元素（记录），这是最好的情况。
• 最差时间复杂度：$O(n^2)$。最差的情况下（初始时区间已经是降序排列），每个元素 $nums[i]$ 都要进行 $i - 1$ 次元素之间的比较，元素之间总的比较次数达到最大值，为 $∑^n_{i=2}(i − 1) = \frac{n(n−1)}{2}$。
• 平均时间复杂度：$O(n^2)$。如果区间的初始情况是随机的，即参加排序的区间中元素可能出现的各种排列的概率相同，则可取上述最小值和最大值的平均值作为插入排序时所进行的元素之间的比较次数，约为 $\frac{n^2}{4}$。由此得知，插入排序算法的平均时间复杂度为 $O(n^2)$。
• 空间复杂度：$O(1)$。插入排序算法为原地排序算法，只用到指针变量 $i$、$j$ 以及表示无序区间中第 $1$ 个元素的变量等常数项的变量。
• 排序稳定性：在插入操作过程中，每次都讲元素插入到相等元素的右侧，并不会改变相等元素的相对顺序。因此，插入排序方法是一种 稳定排序算法。