Skip to content

Latest commit

 

History

History
312 lines (224 loc) · 9.18 KB

20220508.md

File metadata and controls

312 lines (224 loc) · 9.18 KB
Raw

鉄道旅行 (Railroad Trip)

题目描述

JOI国有 $N$ 个城市，编号从 $1$ 到 $N$ ；另外，有 $N−1$ 条铁路，编号从 $1$ 到 $N−1$ ，其中第 $i$ 条 $(1\le i\le N-1)$ 铁路双向连接城市 iii 和城市 $i+1$ 。
乘坐 JOI 国家的铁路有两种方法：用纸质车票乘车或用 IC 卡乘车。
用纸质车票在铁路 $i$ 上乘车的费用为 $A_i$ ，用 IC 卡在铁路 $i$ 上乘车的费用为 $B_i$ 。但是要用 IC 卡在铁路铁路 $i$ 上乘车，必须先购买铁路 $i$ 可以使用的 IC 卡。购买铁路 $i$ 可以使用的 IC 卡需要 $C_i$ 日元。购买一次 IC 卡就可以多次使用。
由于 IC 卡的金额处理比较简单，所以用 IC 卡乘车时的费用比用纸质车票乘车时的费用便宜。也就是说，对于所有 $1 \le i \le n-1$ ，都满足 $A_i \gt B_i$ 。由于 IC 卡的规定在每条铁路上都不同，所以对于所有 $1 \le i \le n-1$ ，不能在其他铁路上使用铁路 $i$ 可以使用的 IC 卡。
您决定在 JOI 国旅行。从城市 $P_1$ 出发，按照 $P_2,P_3...P_M$ 的顺序访问城市。旅行由 $M−1$ 天的行程组成。其中，在第 $j$ 天 $(1\le j\le M-1)$ ，在铁路上乘车从城市 $P_j$ 移动到城市$P_{j+1}$ 。此时，你可能在不同的铁路上乘车。另外，你可能会去同一个城市两次及以上。
JOI 国的铁路很快，所以你从任意一个城市乘车到任意一个城市只需要一天。现在，你没有任何铁路的 IC 卡。你可以选择预先购买一些铁路的 IC 卡，减少花费在乘车上的费用。
也就是说，你需要规划是否购买 IC 卡，使得购买 IC 卡的费用和乘车费用之和最小。

Solution

按照题意模拟，可以计算出每条路走过的次数。

然后扫一遍，枚举每一条边，分别计算使用 IC 卡所用的花费与不使用 IC 卡的花费。

如果 IC 卡所用的花费大，则不用 IC 卡；反之则不用。

对于 计算出每条路走过的次数 只需要用树状数组/差分维护即可。

代码

#include <bits/stdc++.h>
using namespace std;

long long N , M;

long long P[100010];

struct qwq {
	long long A , B , C;
} Road[100010];

long long C[100010];

long long LowBit(long long x) {
	return x & -x;
}

void _add(int u , int v) {
	while(u <= N) {
		C[u] += v;
		u += LowBit(u);
	}
}

void UpDate(int l , int r) {
	_add(l , 1);
	_add(r + 1 , -1);
}

long long Query(int x) {
	long long res = 0;
	while(x) {
		res += C[x];
		x -= LowBit(x);
	}
	return res;
}

int Now;

long long Ans;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	
	cin >> N >> M;
	for(int i = 1; i <= M; i++) {
		cin >> P[i];
	}
	
	Now = P[1];
	
	for(int i = 1; i < N; i++) {
		cin >> Road[i].A >> Road[i].B >> Road[i].C;
	}
	
	for(int i = 2; i <= M; i++) {
		if(P[i] == Now) continue;
		
		else if(P[i] > Now) {
			UpDate(Now , P[i] - 1);
			Now = P[i];
		}
		
		else {
			UpDate(P[i] , Now - 1);
			Now = P[i];
		}
	}

	for(int i = 1; i < N; i++) {
		long long ToT = Query(i);
		if(ToT * Road[i].A > ToT * Road[i].B + Road[i].C) {
			Ans += ToT * Road[i].B + Road[i].C;
		}
		else {
			Ans += ToT * Road[i].A;
		}
	}
	
	cout << Ans <<endl;
	return 0;
}

ケーキの切り分け２ (Cake 2)

题目描述

JOI 君和 IOI 酱是双胞胎兄妹。 JOI 君最近闲暇时常常会做甜点。今天 JOI 君也烤了蛋糕吃，IOI 酱立马嗅到了蛋糕的香气于是跑来想分着吃。
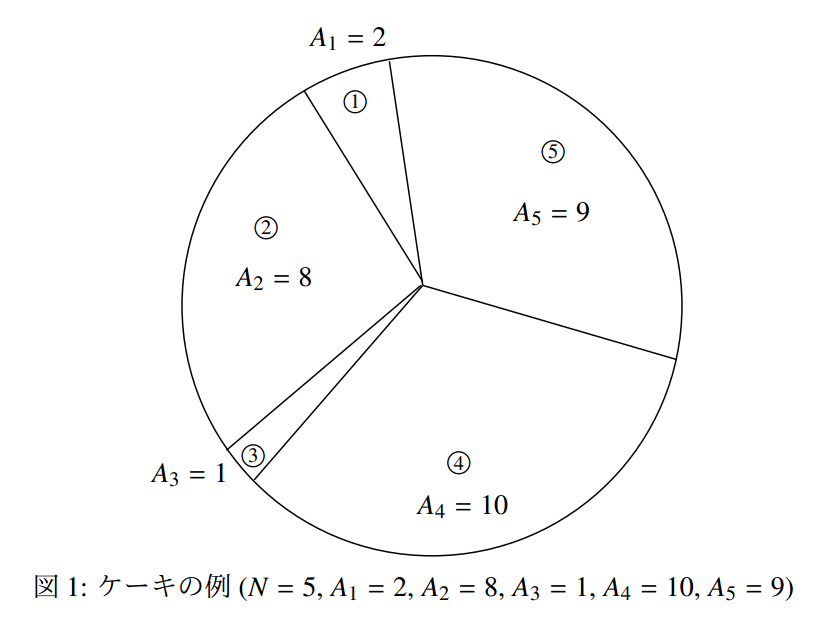
蛋糕是圆形的，从蛋糕中某点开始将蛋糕放射状切为 $ N $ 块，按逆时针顺序编号为 $ 1 $ 到 $ N $ 。也就是说，对任意 $ i $ 来说 $ (1 \leq i \leq N) $ ，第 $ i $ 块蛋糕紧挨着第 $ i-1 $ 块与第 $ i+1 $ 块（不过第 $ 0 $ 块相当于第 $ N $ 块，第 $ N+1 $ 块相当于第 $ 1 $ 块）。第 $ i $ 块蛋糕的大小为 $ A_i $ 。由于切蛋糕的人刀功很不好，所以 $ A_i $ 互不相同。

JOI 君和 IOI 酱按照以下的方法分这 $N$ 块蛋糕：

  1. 首先 JOI 君从这 $ N $ 块蛋糕中任选一块取走；
  2. 然后，从 IOI 酱开始， IOI 酱和 JOI 君交替地从剩下的蛋糕中选出一块取走。不过，当且仅当一块蛋糕两旁的蛋糕至少有一块已经被选择，这块蛋糕才能被选择。如果可供选择的蛋糕有多个， IOI 酱会选择最大的一个，而 JOI 君可以任选一个。

JOI 君想让自己所得到的蛋糕大小的合计值最大。

Solution

乍一看就知道是区间 DP

定义 $f_{i , j}$ 表示区间 $[i,j]$ 中 JOI君 得到的蛋糕大小的总和的最大值。

如果当前对应的这一段区间 $[l,r]$ 是奇数，表示现在是 JOI君 取，那么它可以在序列两端取，即 $[l+1,r]$ 和 $[l,r-1]$ 加上取的数。

如果当前对应的这一段区间 $[l,r]$ 是偶数，表示现在是 IOI君 取，但是她只会取较大的。那么当 $Num_l \ge Num_{r + 1}$ 时，我们才可以从区间 $[l+1 , r]$ 转移；同理，当 $Num_r \ge Num_{l - 1}$ 时，我们才可以从区间 $[l , r - 1]$ 转移

由于是一个环，我们破环成链即可。

$$ f_{l,r} =\left{ \begin{array}{lc} (r-l+1) \ is \ odd \ \ \ \ \ \max\left{ \begin{array}{lc} f_{l+1 , r} + Num_l\\ f_{l , r - 1} + Num_r \end{array} \right.\\ (r-l+1) \ is \ even \ \ \ \max\left{ \begin{array}{lc} f_{l+1,r} \ \ \ Num_l \ge Num_{r + 1}\\ f_{l,r-1} \ \ \ Num_r \ge Num_{l - 1} \end{array} \right. \end{array} \right. $$

代码

#include <bits/stdc++.h>
using namespace std;

unsigned long long Num[4010] , Dp[4010][4010] , Ans , N;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	
	cin >> N;
	for(int i = 1; i <= N; i++) {
		cin >> Num[i];
		Num[i + N] = Num[i];
	}
	
	for(int i = 1; i <= 2 * N; i++) {
		Dp[i][i] = Num[i];
	}
	
	Num[0] = Num[N];
	
	for(int Len = 2; Len <= N; Len++) {
		for(int l = 1; l + Len - 1 <= N * 2; l++) {
			int r = l + Len - 1;
			if(Len & 1) {
				Dp[l][r] = max(Dp[l + 1][r] + Num[l] , Dp[l][r - 1] + Num[r]);
			}
			else {
				Dp[l][r] = max(Num[l] >= Num[r + 1] ? Dp[l + 1][r] : 0 , Num[r] >= Num[l - 1] ? Dp[l][r - 1] : 0);
			}
		}
	}
	
	for(int i = 1; i <= N; i++) {
		Ans = max(Ans , Dp[i][i + N - 1]);
	}
	
	cout << Ans << endl;
	return 0;
}

JOI 公園 (JOI Park)

题目描述

时值 $ 20\text{XX} $ 年， IOI 国为了给办奥赛做准备，将要修缮 IOI 国中的 JOI 公园。 JOI 公园里有 $ N $ 个广场，这些广场从 $ 1 $ 到 $ N $ 编号。有 $ M $ 条道路连接各个广场，这些道路从 $ 1 $ 到 $ M $ 编号。第 $ i(1 \leq i \leq M) $ 条道路是一条连接第 $ A_i $ 和第 $ B_i $ 个广场的双向边，长度为 $ D_i $ 。任意两个广场间一定有道路（直接或间接）相连。

修缮计划如下：首先，选择一个自然数 $ X $ ，将和第一个广场距离等于 $ X $ 或在 $ X $ 以下的所有广场（含第一个广场）相互之间连结一条地下通道。广场 $ i $ 和广场 $ j $ 的距离指，从广场 $ i $ 到广场 $ j $ 经过的道路长度总和的最小值。定义 $ C $ 为一个与修筑地下通道花费有关的量（ $ C $ 是整数）。修筑所有地下通道的花费为 $ C\times X $ 。

接下来，撤去已经通过地下通道连接的广场之间的道路。撤去道路的花费不计。

最后，将没有被撤去的道路进行修补，长为 $ d $ 的道路修补的花费为 $ d $ 。

修缮计划实施之前， JOI 公园没有地下通道。请求出 JOI 公园修缮花费总和的最小值。

Solution

首先，我们很显然要跑一边最短路，并且将最短路从小到大排序。记此时的最短路排完序后的数组为 $Dist$。

显然的，$x \in Dist$，这个证明很显然。我们只需要按照 $Dist$ 的顺序枚举 $X$ ，设当前枚举在第 $i$ 位。接下来模拟即可。

代码

#include <bits/stdc++.h>
using namespace std;

#define int long long

const int MAXN = 1e5 + 10;

vector<pair<int , int> > G[MAXN];
int Dist[MAXN];
int Id[MAXN];

bool Book[MAXN];

int N , M , C;

int Sum = 0;

int Ans = 30000000000ll;

void SP() {
	for(int i = 1; i <= N; i++) Dist[i] = 30000000000ll;
	Dist[1] = 0;	
	
	priority_queue<pair<int, int> > q;
	q.push({0 , 1});
	
	while(q.size()) {
		int x = q.top().second;
		q.pop();
		if(Book[x]) continue;
		Book[x] = true;
		
		for(auto i : G[x]) {
			if(Dist[i.first] > Dist[x] + i.second) {
				Dist[i.first] = Dist[x] + i.second;
				q.push({-Dist[i.first] , i.first});
			}
		}
	}
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	
	cin >> N >> M >> C;
	
	for(int i = 1 , u , v , w; i <= M; i++) {
		cin >> u >> v >> w;
		G[u].push_back({v , w});
		G[v].push_back({u , w});
		
		Sum += w;
	}
	
	for(int i = 1; i <= N; i++) {
		Id[i] = i;
	}

	SP();
	
	memset(Book , 0 , sizeof Book);
	
	sort(Id + 1 , Id + 1 + N , [=](int a , int b) {return Dist[a] < Dist[b]; });

	sort(Dist + 1 , Dist + 1 + N);
	
	for(int i = 1; i <= N; i++) {
		for(auto j : G[Id[i]]) {
			if(Book[j.first] == true) {
				Sum -= j.second;
			}
		}
		Book[Id[i]] = true;
		Ans = min(Ans , C * Dist[i] + Sum);
	}
	
	cout << Ans << endl;
	return 0;
}